Параллельные прямые перпендикулярные плоскости распределите пары прямая плоскость по категориям (8 видео)

Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости

Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.

Содержание

Перпендикулярные прямая и плоскость – основные сведения
Перпендикулярность прямой и плоскости – признак и условия перпендикулярности
Геометрия. 10 класс
Параллельны
Перпендикулярны
Лекция по математике на тему «Параллельные прямые, перпендикулярные к плоскости»
«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Математика: теория и методика преподавания в образовательной организации
Оставьте свой комментарий
Подарочные сертификаты
📹 Видео

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Перпендикулярные прямая и плоскость – основные сведения

Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.

Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.

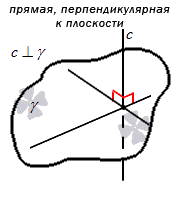
Перпендикулярность обозначается « ⊥ ». Если в условии задано, что прямая с перпендикулярна плоскости γ , тогда запись имеет вид с ⊥ γ .

Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.

При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен 90 градусов.

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Перпендикулярность прямой и плоскости – признак и условия перпендикулярности

Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.

Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.

Подробное доказательство приведено в учебнике геометрии 10 — 11 класса. Теорема применяется для решения задач, где необходимо установить перпендикулярность прямой и плоскости.

При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.

Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.

Для того, чтобы прямая а была перпендикулярна плоскости γ , необходимым и достаточным условием является коллинеарность направляющего вектора прямой а и нормального вектора плоскости γ .

При a → = ( a x , a y , a z ) являющимся вектором прямой a , при n → = ( n x , n y , n z ) являющимся нормальным вектором плоскости γ для выполнения перпендикулярности нужно, чтобы прямая a и плоскость γ принадлежали выполняемости условия коллинеарности векторов a → = ( a x , a y , a z ) и n → = ( n x , n y , n z ) . Отсюда получаем, что a → = t · n → ⇔ a x = t · n x a y = t · n y a z = t · n z , t является действительным числом.

Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.

Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.

Доказать перпендикулярность заданной прямой x 2 — 1 = y — 1 2 = z + 2 2 — 7 с плоскостью x + 2 2 + 1 y — ( 5 + 6 2 ) z .

Знаменатели канонических уравнений являются координатами направляющего вектора данной прямой. Отсюда имеем, что a → = ( 2 — 1 , 2 , 2 — 7 ) является направляющим вектором прямой x 2 — 1 = y — 1 2 = z + 2 2 — 7 .

В общем уравнении плоскости коэффициенты перед переменными x , y , z являются координатами нормального вектора данной плоскости. Отсюда следует, что n → = ( 1 , 2 ( 2 + 1 ) , — ( 5 + 6 2 ) ) — это нормальный вектор плоскости x + 2 2 + 1 y — ( 5 + 6 2 ) z — 4 = 0

Необходимо произвести проверку выполнимости условия. Получаем, что

2 — 1 = t · 1 2 = t · 2 ( 2 + 1 ) 2 = t · ( — ( 5 + 6 2 ) ) ⇔ t = 2 — 1 , тогда векторы a → и n → связаны выражением a → = ( 2 — 1 ) · n → .

Это и есть коллинеарность векторов. отсюда следует, что прямая x 2 — 1 = y — 1 2 = z + 2 2 — 7 перпендикулярна плоскости x + 2 ( 2 + 1 ) y — ( 5 + 6 2 ) z — 4 = 0 .

Ответ: прямая и плоскость перпендикулярны.

Определить, перпендикулярны ли прямая y — 1 = 0 x + 4 z — 2 = 0 и плоскость x 1 2 + z — 1 2 = 1 .

Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.

Из прямой y — 1 = 0 x + 4 z — 2 = 0 видно, что направляющий вектор a → — это произведение нормальных векторов плоскости y — 1 = 0 и x + 4 z — 2 = 0 .

Отсюда получаем, что a → = i → j → k → 0 1 0 1 0 4 = 4 · i → — k → .

Координаты вектора a → = ( 4 , 0 , — 1 ) .

Уравнение плоскости в отрезках x 1 2 + z — 1 2 = 1 является эквивалентным уравнению плоскости 2 x — 2 z — 1 = 0 , нормальный вектор которой равен n → = ( 2 , 0 , — 2 ) .

Следует произвести проверку на коллинеарность векторов a → = ( 4 , 0 , — 1 ) и n → = ( 2 , 0 , — 2 ) .

Для этого запишем:

4 = t · 2 0 = t · 0 — 1 = t · ( — 2 ) ⇔ t = 2 t ∈ R ⇔ t ∈ ∅ t = 1 2

Отсюда делаем вывод о том, что направляющий вектор прямой не коллинеарен нормальному вектору плоскости. Значит, y — 1 = 0 x + 4 z — 2 = 0 — это прямая, не перпендикулярная к плоскости x 1 2 + z — 1 2 .

Ответ: прямая и плоскость не перпендикулярны.

Видео:ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать

Геометрия. 10 класс

Прямая, перпендикулярная к плоскости

Соберите из тайлов изображение.

Перпендикулярность прямой и плоскости

Подпишите каждое изображение, в каком доказательстве оно используется?

Перпендикулярность прямой и плоскости

Выберите ребра, перпендикулярные плоскости DCС₁.

Перпендикулярные прямые в пространстве

Закончите предложения, чтобы получилось верное утверждение, установив соответствие между элементами.

Параллельные прямые, перпендикулярные плоскости

Распределите пары «прямая-плоскость» по категориям.

Параллельны

Перпендикулярны

Признак параллельности прямой и плоскости

Подчеркните лишние элементы в решение задачи

Дано: точка М лежит вне плоскости АВС, $angle MAC=90^0$, $angle BAC=90^0$.

Доказать, что прямая АС перпендикулярна плоскости АМВ.

$AC perp AB$ (по условию), $AC perp AM$ (по условию)

$AB subset (AMB)$, (AMC);

$AM subset (AMB)$, (AMC);

$AB subset AM$ = А, В,

следовательно $AC perp (АМВ)$, (АМС) (по признаку параллельности прямой и плоскости.

Что и требовалось доказать.

Прямая, перпендикулярная к плоскости

Точки A, М и О лежат на прямой a, перпендикулярной к плоскости α, а точки О, B, С и D лежат в плоскости α. Какие из следующих углов являются прямыми: АОВ, МОС, DAM, DOA, BMO?

Прямая a ⊥ , поэтому прямая a перпендикулярна к любой прямой лежащей в плоскости . Чтобы прямая плоскости α, необходимо, чтобы точки прямой принадлежали плоскости α.

Перпендикулярность прямой и плоскости

Выберите верные утверждения

В кубе $ABCDA_ B_ C_ D_$ проведено сечение плоскостью $A_ B_C$. Тогда:

Угол между секущей плоскостью и плоскостью $ABC$ равен углу $BCA_$.

Плоскость $CBB_$ перпендикулярна линии пересечения секущей плоскости и плоскости $ABC$.

Углом между секущей плоскостью и прямой $AC$ является угол между прямыми $AС$ и $A_C$.

Угол между секущей плоскостью и плоскостью $ABC$ равен $45^$.

Прямоугольный параллелепипед

Укажите верные и неверный свойства, которыми обладает прямоугольный параллелепипед. Для каждого утверждения укажите: да или нет

Сумма плоских углов при вершине равна 270°

Все три измерения равны

Все грани – прямоугольники

Диагонали пересекаются в одной точке и делятся этой точкой пополам

Диагонали перпендикулярны основаниям

Все диагонали равны

Свойства прямоугольника

Прямая РQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках Р₁ и Q₁. Докажите, что PQ = P₁Q₁.

Выберите элементы, пропущенные в тексте.

Две прямые и перпендикулярны к одной и той же плоскости α. Значит, эти прямые параллельны между собой. Пусть через них проходит плоскость β. В плоскости β прямые PQ и P₁Q₁ параллельны, так как по условию PQ параллельна α.

Рассмотрим прямоугольник . В прямоугольнике РР₁Q₁Q противоположные стороны равны, значит, PQ = P₁Q₁, что и требовалось доказать.

Перпендикулярность прямой и плоскости

Решите задачу. Запишите ответ.

Проведенная к плоскости перпендикулярная прямая пересекает плоскость в точке O.

На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка.

Определи вид и периметр треугольника ABD, если AD = 4 см, а OB = 2 см (ответ округли до одной десятой).

Прямая, перпендикулярная к плоскости

Введите правильные данные в решение задачи.

Плоскости α и β пересекаются по прямой а. Из точки М проведены перпендикуляры МА и МВ соответственно к плоскостям α и β. Прямая a пересекает плоскость АМВ в точке С. Докажите, что МС ⊥ a.

Прямая МА плоскости α. Прямая а в плоскости α. Значит, прямая МА перпендикулярна прямой а.

Прямая МB плоскости β. Прямая а лежит в плоскости β. Значит, прямая МB перпендикулярна прямой а.

Прямая а перпендикулярна двум прямым из плоскости АВМ. Значит, прямая а перпендикулярна плоскости АВМ. Прямая СМ лежит в плоскости АВМ. Значит, прямой МС, что и требовалось доказать.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Лекция по математике на тему «Параллельные прямые, перпендикулярные к плоскости»

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Лекция по теме «Параллельные прямые, перпендикулярные к плоскости»

Попробуем ответить на вопрос: Когда прямая перпендикулярна плоскости. Для этого рассмотрим модель параллелепипеда АВС D А ₁ В ₁ С ₁ D ₁ в основании, которого лежит квадрат.

Например, попробуем найти прямую перпендикулярную плоскости АВС D . Рассмотрим прямую А ₁ В.

Очевидно, что угол между прямой А ₁ В и прямой АВ острый, а вот прямая ВС и прямая А ₁ В перпендикулярны, как стороны диагонального сечения А ₁ ВС D ₁ . Заметим, что прямые АВ и ВС пересекаются.

Рассмотрим прямую С ₁ С . Прямая С ₁ С перпендикулярна прямой ВС.

Одновременно прямая С ₁ С перпендикулярна и прямой D С лежащей в плоскости А ₁ ВС D ₁ . Заметим так же, что прямые D С и ВС пересекаются.

Рассмотрим еще один вариант расположения прямых. Пусть диагонали основания пересекаются в точке О, и по свойству квадрата отрезок D О равен отрезку О B . Прямая С ₁ О перпендикулярна прямой D В по свойству равнобедренного треугольника DC ₁ В. Но С ₁ О не перпендикулярна прямой АС.

Какой же из вариантов определяет прямую перпендикулярную плоскости.

В геометрии прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Таким образом прямая А ₁ В не удовлетворяет условию, она не перпендикулярна прямой АВ, лежащей в плоскости АВС D .

Аналогично и с рисунком в). Прямая ОС ₁ не перпендикулярна прямой АС, лежащей в плоскости АВС D .

А рисунок б) демонстрирует перпендикулярность прямой и плоскости.

На письме перпендикулярность прямой С ₁ С и плоскости АВС D так.

На экране изображение и текст:

Когда прямая перпендикулярна плоскости?

На экране обновляется изображение с анимацией плоскости и прямой.

Изображение обновляется с анимацией прямой и отметок углов.

На экране изображение с анимацией элементов

На экране изображение

На экране текст :

Прямая называется перпендикулярной к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости.

На экране рисунок а) выделяется и исчезает.

На экране рисунок в) выделяется и исчезает.

На экране текст и изображение:

К изображению справа добавляется надпись

Помимо прямой С ₁ С к плоскости АВС D в данном параллелепипеде перпендикулярны и рёбра А ₁ А, D ₁ D , В ₁ В.

Это можно доказать аналогично ребру С ₁ С. При этом они параллельны между собой.

На экране изображение

Связь прямых и плоскости сформулирована в двух важных теоремах. Докажем их.

Теорема 1. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.

Для доказательства рассмотрим две параллельные прямые a и b , и плоскость α . Прямая а перпендикулярна плоскости α по условию.

Докажем, что прямая b перпендикулярна плоскости α .

1)Для доказательства проведём в плоскости α произвольную прямую с .

2)Так как прямая а у нас перпендикулярна плоскости α , то по определению она перпендикулярна произвольной прямой с лежащей в этой плоскости.

3)По теореме, доказанной на предыдущем уроке, если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна к этой прямой, т.е. прямые b и с перпендикулярны.

4)Аналогично можно доказать, что прямая b будет перпендикулярна любой другой прямой, лежащей в плоскости α.

Что доказывает перпендикулярность прямой b к любой прямой плоскости , тогда по определению прямой перпендикулярной плоскости, прямая b перпендикулярна плоскости α .

На экране текст теоремы:

Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.

На экране изображение:

На экране изображение и текст постепенно обновляется, добавляется пункт 1):

На экране добавляется последняя часть текста пункт 3)

На экране обновляется изображение с анимацией произвольных прямых..

К изображению и тексту добавляется пункт 4)

так как прямая b перпендикулярна любой прямой плоскости α, то .

Для данного утверждения справедлива и обратная формулировка.

На экране текст:

Обратная теорема : Если две прямые перпендикулярны к плоскости, то они параллельны.

Достаточно интересно посмотреть применение данных теорем для решения задач.

Дан параллелепипед АВС D А ₁ В ₁ С ₁ D ₁ c углом ВА D равным 90 градусов.

1)У нас угол ВА D равен 90 градусов, значит АВС D – прямоугольник.

2,3)Таким образом прямая DC перпендикулярна прямой ВС, и прямая D С перпендикулярна прямой СС ₁ , так как боковые грани прямоугольного параллелепипеда прямоугольники.

4)Так как прямая DC перпендикулярна прямым ВС и С ₁ С плоскости В ₁ ВСС ₁ , то по определению прямая D С перпендикулярна самой плоскости В ₁ ВСС ₁ .

5)Прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости. В данном случае прямая DC перпендикулярная прямой В ₁ С ₁ .

На экране текст задачи:

Задача. Дан прямоугольный параллелепипед АВС D А ₁ В ₁ С ₁ D ₁ с ВА D =90°.

На экране изображение и текст.

Доказательство на экране добавляется пунктом 1):

так как ВА D =90°, то АВС D -прямоугольник.

Доказательство на экране добавляется пунктом 2) , 3)

DC ВС (по свойству прям-ка)

DC С ₁ С (по свойству прям-го парал-да)

Доказательство на экране добавляется пунктом 4)

Доказательство на экране добавляется пунктом 5)

Рассмотри ещё один пример применения терем к решению задач.

Нам дана плоскость α, отрезок АВ пересекает эту плоскость в точке О. Прямые АА ₁ и ВВ ₁ перпендикулярны к плоскости α, причём А ₁ и В ₁ лежат в плоскости. Известно, что АА ₁ 4 см, а угол А ₁ АО =60° и отрезок В ₁ О относиться к отрезку А ₁ О как 1 к 2.

1)Прямая А ₁ В ₁ лежит в плоскости α, так как две точки прямой уже лежат в плоскости.

2)Прямые АА ₁ и ВВ ₁ перпендикулярны к плоскости α, тогда эти прямые перпендикулярна любой прямой лежащей в плоскости α, в частности прямой А ₁ В ₁ .

3)Тогда треугольники АА ₁ О и ОВ ₁ В прямоугольные.

4)В треугольнике угол АОА ₁ равен 30°, по свойству треугольника с таким углом катет АА ₁ равен половине гипотенузы, значит отрезок АО равен 8 см.

5)В треугольниках АА ₁ О и ОВ ₁ В угол АА ₁ О равен углу ОВ ₁ В, угол А ₁ ОА равен углу ВОВ ₁ по свойству вертикальных углов, а стороны В ₁ О и ОА ₁ пропорциональны числам 1 и 2, значит треугольник АА ₁ О подобен треугольнику ОВ ₁ В по стороне и двум прилежащим к ней углам с коэффициентом подобия одна вторая.

6,7)Так как треугольники подобны, то ОВ относиться к стороне АО как 1 к 2. Получим, что сторона ОВ равна половине стороны АО и равна 4 см. А весь отрезок АВ состоящий из частей АО и ОВ равен 12 см.

На экране текст задачи:

Задача 2. Отрезок АВ пересекает плоскость α в точке О. Прямые АА ₁ и ВВ ₁ перпендикулярны плоскости α т пересекают её в точках А ₁ и В ₁ соответственно.

Найдите АВ, если А ₁ А= 4см, А ₁ АО =60°, В ₁ О: ОА ₁ =1:2

На экране появляется чертёж и текст:

К чертежу справа добавляется пункт решения:

К чертежу справа добавляется пункт решения и обновляется чертёж:

К чертежу справа добавляется пункт решения:

4) ΔАА ₁ О: АОА ₁ =30°, значит АО=2АА ₁ =8 см.

На экране обновляется чертёж и добавляется пункт решения:

К чертежу справа добавляется пункт решения6) и 7) :

Видео:16. Параллельные прямые, перпендикулярные к плоскостиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 966 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 690 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Стринкевич Лилия ИльфатовнаНаписать 479 15.12.2016

Номер материала: ДБ-025618

15.12.2016 407

15.12.2016 296

15.12.2016 455

15.12.2016 638

15.12.2016 1830

15.12.2016 322

15.12.2016 346

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.