Параллельные прямые и плоскости в пространстве тест

Тесты по геометрии 10 класс. Тема: «Параллельность прямых и плоскостей»

Правильный вариант ответа отмечен знаком +

1. Какими называют плоскость и прямую, не имеющих ни одной общей точки?

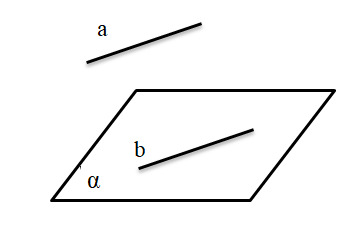
2. Посмотрите на рисунок и выберите правильное утверждение:

— Прямая а и плоскость α являются перпендикулярными.

— В плоскости α находится прямая а.

— Плоскость α и прямая b являются перпендикулярными.

+ Плоскость α и прямая а являются параллельными друг другу.

3. Сколько случаев взаимного расположения прямой и плоскости в пространстве имеется?

4. В каком варианте ответа указано правильное суждение?

— Не находящаяся в данной плоскости прямая считается параллельной этой плоскости, если она пересекается с какой-либо прямой, находящейся на этой плоскости.

+ Если прямая не принадлежит данной плоскости и является параллельной какой-либо прямой на этой плоскости, то она считается параллельной данной плоскости.

— Не находящаяся в данной плоскости прямая, которая является параллельной лежащей на этой плоскости прямой, считается перпендикулярной данной плоскости.

— Если прямая не принадлежит данной плоскости и является перпендикулярной какой-либо лежащей на этой плоскости прямой, то она считается параллельной данной плоскости.

5. Через сколько точек можно провести лишь одну плоскость?

— невозможно провести только одну плоскость

6.Если прямая K и плоскость α обладают одной общей точкой, то это значит, что:

— плоскость α и прямая K характеризуются параллельностью между собой.

+ плоскость α и прямая K пересекаются.

— прямая K находится в плоскости α.

— прямая K параллельна другой прямой, лежащей в плоскости α.

7. Плоскости S и T пересекаются третьей плоскостью U. Из этого следует, что:

— плоскости S и T перпендикулярны плоскости U.

— плоскости S и U являются параллельными.

— плоскости T и U являются параллельными.

+ линии пересечения плоскостей являются параллельными.

8. Выберите правильное утверждение:

+ При условии, что плоскость проходит через данную прямую, являющуюся параллельной другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей всегда параллельна данной прямой.

— Чтобы линия пересечения плоскостей была параллельна прямой, плоскость должна проходить через прямую, являющуюся перпендикулярной другой плоскости, и пересекать эту плоскость.

— Если линия пересечения плоскостей параллельна данной прямой, то плоскость проходит через эту прямую, являющуюся параллельной другой плоскости, и не пересекает эту плоскость.

— Чтобы линия пересечения плоскостей была перпендикулярна прямой, плоскость должна проходит через прямую, являющуюся параллельной другой плоскости, и пересекать эту плоскость.

9. Каких плоскостей называют параллельными?

тест 10. Даны две параллельные между собой прямые Y и Z. Одна из них, а именно прямая Z, параллельна данной плоскости. Значит, прямая Y:

— не принадлежит данной плоскости или является ей перпендикулярной.

— и данная плоскость являются скрещивающимися или она лежит в этой плоскости.

+ находится в данной плоскости или параллельна этой плоскости.

— параллельна данной плоскости или не лежит этой плоскости.

11. У плоскости α и прямой D множество общих точек. Это обозначает, что:

— плоскость α и прямая D являются перпендикулярными.

— плоскость α и прямая D пересекаются в одной точке.

— прямая D и плоскость α параллельны между собой.

+ прямая D находится в плоскости α.

12. В плоскости α лежит основа BC треугольника ABC. Точка P является серединой основы BC. Выберите правильное суждение:

— Прямые AP и BC являются параллельными.

— Прямая AP и плоскость α являются параллельными.

+ Прямая CP находится в плоскости α.

— Прямые AP и BC не пересекаются.

13. В каких случаях плоскостей можно считать параллельными?

+ При условии, что две находящиеся в одной плоскости пересекающиеся прямые параллельны двум лежащим в другой плоскости пересекающимся прямым.

— При условии, что две лежащие в разных плоскостях параллельные прямые перпендикулярны двум находящимся в другой плоскости параллельным прямым.

— При условии, что две пересекающиеся и находящиеся в одной плоскости прямые перпендикулярны двум лежащим в другой плоскости пересекающимся прямым.

— При условии, что одна находящаяся в одной плоскости прямая пересекается с другим лежащим в другой плоскости прямым.

14. Есть три плоскости F, L, O. Плоскость F является параллельной плоскости O, плоскость L – параллельной плоскости O. Исходя из этого выберите правильное утверждение:

— Плоскость F и плоскость L перпендикулярны.

— Плоскость F и плоскость L являются скрещивающимися.

+ Плоскость F и плоскость L параллельны.

— У плоскости F и плоскости L есть одна точка пересечения.

15. При условии, что прямые P и R параллельны третьей прямой Q,:

— прямая P будет перпендикулярна прямой R.

— прямая P и прямая R будут иметь одну точку пересечения.

— прямые P и R будут скрещивающимися.

+ прямые P и R будут параллельны между собой.

16. Есть две параллельные прямые и две параллельные плоскости. Между двумя данными плоскостями находятся отрезок XX1 и отрезок ZZ1 параллельных прямых. Выберите правильное утверждение:

— XX1 и ZZ1 имеют точку пересечения

17. Сколько параллельных прямых можно провести через точку, находящуюся вне данной прямой?

18. В каком варианте представлен ответ с ошибочным суждением?

— Две плоскости считаются параллельными, если каждая из них параллельна третьей плоскости.

— Две параллельные линии могут образоваться в результате пересечения двух параллельных плоскостей третьей плоскостью.

+ Две пересекающиеся прямые, находящиеся в одной плоскости, называются параллельными.

— Отрезки двух параллельных прямых, заключенные между двумя параллельными плоскостями, всегда равны друг другу.

19. Дана трапеция ABCD, основа CD которой лежит в плоскости α. KN – средняя линия трапеции. Выберите вариант ответа, в котором указано правильное суждение:

— KN находится в плоскости α.

+ KN параллельна плоскости α.

— KN перпендикулярна плоскости α.

-KN параллельна AD.

тест-20. Точка N находится вне данной плоскости. Можно ли через нее провести плоскость, параллельную данной? Если да, то сколько?

21. Выберите вариант ответа, в котором представлено правильное продолжение следующего утверждения: «Если S – это середина стороны AB треугольника ABC, сторона AC которого находится в плоскости α, то . »:

— через точку S можно провести две прямые, которые будут параллельны плоскости α.

— прямая SC и плоскость α перпендикулярны.

+ через точку S можно провести лишь одну параллельную плоскости α плоскость.

— через точку S нельзя провести прямую, которая будет перпендикулярна плоскости α.

22. Прямая H лежит вне плоскости a и является параллельной с прямой J, которая находится в данной плоскости. Выберите ошибочное суждение:

— Прямая H и прямая J не пересекаются.

+ Прямая H и прямая J перпендикулярны.

— Прямая J и плоскость a параллельны.

— Прямая H параллельна плоскости a.

23. Выберите ошибочное утверждение:

+ У прямой и плоскости может быть лишь одна общая точка.

— Две параллельные плоскости никогда не будут пересекаться.

— В одной плоскости могут лежать любые пять точек.

— В одной плоскости могут находиться две параллельные прямые.

24. Прямая M и плоскость α не имеют ни одну общую точку. Это значит, что:

— прямая M пересекается с другой прямой, лежащей в плоскости α.

— прямая M и плоскость α пересекаются.

— в плоскости α лежит прямая M.

+ плоскость α и прямая M параллельны.

25. Что является пересечением двух плоскостей в пространстве?

26. Выберите вариант ответа, в котором неправильно указано продолжение следующей фразы: «Плоскость α и β являются параллельными между собой. Прямая K не лежит в плоскости α»:

+ Прямая K и плоскость β имеют одну общую точку пересечения.

— Прямая K лежит в плоскости β.

— Прямая K и плоскость β являются параллельными.

— Прямая K и плоскость α являются параллельными.

27. Какими могут быть две плоскости в пространстве?

— пересекающимися или скрещивающимися

+ параллельными или пересекающимися

28. Плоскость β пересекается с плоскостью α. Выберите правильное утверждение:

— Плоскость β перпендикулярна линии пересечения плоскостей α и β.

— Плоскость α является перпендикулярной линии пересечения плоскостей α и β.

— Плоскость β и плоскость α являются параллельными.

+ Одна из этих плоскостей параллельна линию пересечения плоскостей α и β.

29. Выберите вариант ответа, в котором указано неправильное продолжение следующей фразы: «Боковые стороны треугольника ABC параллельны плоскости β. Значит, . »:

+ основание треугольника и плоскость β пересекаются.

— плоскость треугольника и плоскость β параллельны.

— основание треугольника и плоскость β являются параллельными.

— основание треугольника и плоскость β не пересекаются.

тест_30. Посмотрите на рисунок и скажите, сколько параллельных плоскостей можно провести через две прямые?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Тест «Прямые и плоскости в пространстве»

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Методички Педсовета

Раздел «Прямые и плоскости в пространстве» занимает важное место в стереометрии. Тест дает возможность определить уровень усвоения материала и быстро выявить пробелы в знаниях, создает условия для мотивации, повышения интереса к предмету, способствует развитию и совершенствованию самостоятельной деятельности учащихся и устраняет перегрузку домашнего задания.

1) Прямую, перпендикулярную любой прямой в плоскости, называют…

а) наклонной к плоскости;
б) перпендикуляром к плоскости;
в) секущей;
г) лучом.

2) Наклонной к плоскости называют прямую, пересекающую плоскость и…

а) не пересекающую перпендикуляр;
б) лежащую в ней;
в) не имеющую с ней общих точек;
г) не перпендикулярную ей.

3) Параллельными называют плоскости,…

а) не имеющие общих прямых;
б) у которых одна общая точка;
в) у которых две общих точки;
г) не имеющие ни одной общей точки.

4) Прямая, проходящая через основания перпендикуляра и наклонной, называется…

а) секущей;
б) параллельной плоскости;
в) проекцией наклонной на плоскость;
г) перпендикуляром к плоскости.

5) Наклонная перпендикулярна прямой в плоскости, если…

а) перпендикуляр пересекается с проекцией наклонной на плоскость;
б) проекция наклонной параллельна этой прямой;
в) проекция наклонной перпендикулярна этой прямой;
г) прямая совпадает с проекцией наклонной.

6) Если из точки вне плоскости провести к ней перпендикуляр и наклонные, то…

а) перпендикуляр длиннее наклонной;
б) наклонная длиннее перпендикуляра;
в) проекция наклонной короче перпендикуляра;
г) наклонная и ее проекция равны.

7) Прямая параллельна плоскости, если они…

а) пересекают прямую в одной и той же точке;
б) перпендикулярны одной и той же прямой;
в) удалены от данной точки на равные расстояния;
г) пересекают плоскость в одной точке.

8) Углом между наклонной и плоскостью называют…

а) угол между наклонной и перпендикуляром;
б) угол между проекцией и перпендикуляром;
в) угол между наклонной и ее проекцией;
г) угол между наклонной и прямой в плоскости.

9) Через… проходит единственная плоскость,

а) две точки;
б) три параллельные прямые;
в) три попарно пересекающиеся прямые;
г) четыре точки.

10) Прямая пересекает плоскость, если прямая и плоскость. . .

а) не имеют ни одной общей точки;
б) имеют две общие точки;
в) имеют только одну общую точку;
г) имеют три общих точки.

11) Если прямая пересекает плоскость квадрата в точке пересечения диагоналей и перпендикулярна двум смежным его сторонам, то она. . .

а) параллельна двум другим сторонам квадрата;
б) перпендикулярна диагоналям квадрата;
в) параллельна диагоналям квадрата;
г) образует с плоскостью квадрата угол в 30 градусов.

12) Если две параллельные плоскости пересечь третьей, то. . .

а) линии пересечения равны;
б) линии пересечения параллельны;
в) линии пересечения перпендикулярны;
г) плоскости совпадают.

13) Если две параллельные плоскости пересечь двумя параллельными прямыми, то…

а) прямые пересекаются в точке;
б) плоскости пересекаются по прямой, параллельной одной из прямых;
в) отрезки, заключенные между плоскостями равны;
г) плоскости перпендикулярны одной из прямых.

14) Если наклонная длиной 16 см образует с плоскостью угол в 60°, то ее проекция на плоскость равна…

а) 32 см;
б) 8 см;
в) 8 cm;
г) 256 см².

15) Наклонные АВ и АС образуют с плоскостью углы в 30° и 45° соответственно. Тогда. . .

а) проекция наклонной АВ длиннее проекции наклонной АС на плоскость;
б) наклонная АВ короче наклонной АС;
в) наклонная АВ длиннее наклонной АС;
г) проекции наклонных равны.

16) Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то…

а) прилежащий катету угол равен 30 градусам;
б) прилежащий катету угол равен 60 градусам;
в) прилежащий катету угол равен 90 градусам;
г) противолежащий угол равен 60 градусам.

17) Перпендикуляром к-плоскости называют прямую, . . .

а) пересекающую плоскость;
б) перпендикулярную некоторой прямой в плоскости;
в) перпендикулярную любой прямой в плоскости;
г) лежащую в параллельной плоскости.

18) Та из наклонных больше, у которой. . .

а) проекция равна перпендикуляру;
б) проекция больше;
в) проекция меньше;
г) проекция больше перпендикуляра.

19) Планиметрия — это измерения. . .

а) углов;
б) отрезков;
в) на плоскости;
г) в пространстве.

20) Угол между наклонной и плоскостью. . .

а) меньше 90 градусов;
б) больше 90 градусов;
в) равен 60 градусам;
г) тупой.

21) Проекцией наклонной на плоскость называют прямую, . . .

а) перпендикулярную плоскости;
б) пересекающую наклонную под углом 30 градусов;
в) проходящую через точки наклонной и перпендикуляра;
г) проходящую через основания наклонной и перпендикуляра.

22) Если две точки прямой принадлежат плоскости, то прямая…

а) называется проекцией точки на плоскость;
б) лежит в плоскости;
в) пересекает плоскость под прямым углом;
г) называется перпендикуляром к плоскости.

23) Прямые, имеющие одну общую точку называют. . .

а) скрещивающимися;
б) пересекающимися;
в) параллельными;
г) совпадающими.

24) Две плоскости параллельны, если они. . .

а) перпендикулярны одной и той же прямой;
б) параллельны одной и той же прямой;
в) пересекаются в одной точке;
г) пересекают одну и ту же прямую.

25) Если две прямые параллельны третьей, то они.

а) перпендикулярны друг другу;
б) параллельны между собой;
в) совпадают;
г) пересекаются.

26) Расстояние между двумя параллельными плоскостями равно 10 см, а отрезок, заключенный между плоскостями равен 12 см. Тогда проекция отрезка на одну из плоскостей равна…

a) см;
б) 44 см;
в) см;
г) 2 см.

27) Две наклонные, длиной 10 см образуют между собой угол в 60 градусов. Расстояние между их проекциями на плоскость равно…

а) 10 см;
б) 5 см;
в) см;
г) 20 см.

28) Две плоскости совпадают, если они имеют. . .

а) две общих точки;
б) три общих точки;
в) одну общую прямую;
г) одну общую точку.

(2 балла)

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Ответы:

1-б, 2-г, 3-г, 4-в, 5-в, 6-б, 7-б, 8-в, 9-в, 10-в, 11-б, 12-б, 13-в, 14-б, 15-а, в,

16-б, 17-в, 18-б, 19-в, 20-а, 21-г, 22-б, 23-б, 24-а, 25-б, 26-а, 27-а, 28-б.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Тест по теме «Параллельность прямых и плоскостей в пространстве» С ОТВЕТАМИ 10 кл

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Тест по теме «Параллельность прямых и плоскостей в пространстве»

1. Пересечением двух плоскостей является

А) точка Б) прямая В) отрезок

2. Сколько должно быть общих точек у прямой с плоскостью, чтобы она лежала в этой плоскости?

А) одна Б) две В) три

3. На сколько множеств разбивает пространство любая плоскость?

А) на два Б) на три В) на четыре

4. Чтобы задать единственную плоскость необходимо

А) две точки Б) три точки

В) три точки, не лежащие на одной прямой

5. Какие из перечисленных фигур задают единственную плоскость в пространстве?

А) две параллельные прямые

Б) две скрещивающиеся прямые

6. Сколько плоскостей задают две пересекающиеся прямые?

А) одну плоскость

Б) две плоскости

В) бесконечно много плоскостей

7. Через какие из перечисленных фигуры можно провести единственную плоскость?

А) Через три точки

Б) Через прямую и не лежащую на ней точку

В) Через отрезок

8. Две прямые пересекаются. Что это значит?

А) Они имеют две общие точки.

Б) Они имеют одну общую точку.

В) Они лежат в одной плоскости.

9. Две прямые называются скрещивающимися, если

А) они не имеют общих точек и не лежат в одной плоскости.

Б) они не имеют общих точек.

В) они имеют одну общую точку.

10. Две прямые в пространстве называются параллельными, если

А) они не имеют общих точек.

Б) они не имеют общих точек и лежат в одной плоскости. В) они не имеют общих точек, и не существует проходящей через них плоскости.

11. Прямая и плоскость не имеют общих точек. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

12. Прямая и плоскость имеют только одну общую точку. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

13. Если две плоскости не имеют общих точек, то они

14. Две плоскости пересекаются. Это значит, что

А) они имеют одну общую точку.

Б) они имеют общую прямую.

В) они имеют общий луч.

15. Укажите свойства параллельных плоскостей

А) Две прямые параллельные третьей прямой, параллельны

Б) Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

В) Отрезки параллельных прямых, заключенные между двумя параллельными

16. Прямолинейные отрезки фигуры изображаются на плоскости чертежа

17. Укажите признак параллельности прямой и плоскости

А) Две прямые параллельные третьей прямой, параллельны

Б) Если две пересекающиеся прямые одной плоскости соответственно параллельны

двум прямым другой плоскости, то эти плоскости параллельны.

В) Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой

в этой плоскости, то она параллельна и самой плоскости.

Тест по теме: «Параллельность прямых и плоскостей в пространстве»

1. Сколько должно быть общих точек у прямой с плоскостью, чтобы она лежала в этой плоскости?

А) одна Б) две В) три

2. Что является пересечением двух плоскостей

А) прямая Б) отрезок В) точка

3. На сколько множеств разбивает пространство любая плоскость?

А) на три Б) на четыре В) на два

4. Сколько плоскостей задают две пересекающиеся прямые?

А) две плоскости

Б) одну плоскость

В) бесконечно много плоскостей

5. Какие из перечисленных фигур задают единственную плоскость в пространстве?

Б) две скрещивающиеся прямые

В) две параллельные прямые

6. Чтобы задать единственную плоскость необходимо

А) две точки Б) три точки

В) три точки, не лежащие на одной прямой

7. Через какие из перечисленных фигуры можно провести единственную плоскость?

А) Через три точки

Б) Через прямую и не лежащую на ней точку

В) Через отрезок

8. Две плоскости пересекаются. Это значит, что

А) они имеют одну общую точку.

Б) они имеют общую прямую.

В) они имеют общий луч.

9. Две прямые называются скрещивающимися, если

А) они не имеют общих точек и не лежат в одной плоскости.

Б) они не имеют общих точек.

В) они имеют одну общую точку.

10. Две прямые в пространстве называются параллельными, если

А) они не имеют общих точек.

Б) они не имеют общих точек и лежат в одной плоскости. В) они не имеют общих точек, и не существует проходящей через них плоскости.

11. Прямая и плоскость не имеют общих точек. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

12. Свойства параллельных плоскостей

А) Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

Б) Две прямые параллельные третьей прямой, параллельны

В) Отрезки параллельных прямых, заключенные между двумя параллельными

13. Прямая и плоскость имеют только одну общую точку. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

14. Две прямые пересекаются. Что это значит?

А) Они имеют две общие точки.

Б) Они лежат в одной плоскости.

В) Они имеют одну общую точку.

15. Если две плоскости не имеют общих точек, то они

16. Прямолинейные отрезки фигуры изображаются на плоскости чертежа

17. Укажите признак параллельности плоскостей

А) Две прямые параллельные третьей прямой, параллельны

Б) Если две пересекающиеся прямые одной плоскости соответственно параллельны

двум прямым другой плоскости, то эти плоскости параллельны.

В) Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой

в этой плоскости, то она параллельна и самой плоскости.

Указать прямые, параллельные прямой

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 338 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Тасимова Айгуль ДжанбулатовнаНаписать 62698 18.11.2017

Номер материала: ДБ-879102

18.11.2017 841

16.11.2017 649

15.11.2017 366

14.11.2017 1306

13.11.2017 310

13.11.2017 312

12.11.2017 963

12.11.2017 242

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

В Липецкой области начинающие педагоги получат 120 тысяч рублей

Время чтения: 0 минут

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Параллельность прямых. 10 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

СТЕРЕОМЕТРИЯ. ВСЕ ЗАДАЧИ НА ПАРАЛЛЕЛЬНОСТЬСкачать

Перпендикулярность прямой и плоскости. 10 класс.Скачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Геометрия 10 класс Параллельность прямых, прямой и плоскости теорияСкачать

Геометрия 10 класс Параллельность прямых, прямой и плоскости практикаСкачать

Параллельность прямой и плоскости. Решение задач по теме Параллельность прямых, прямой и плоскости.Скачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

6. Параллельность прямой и плоскостиСкачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать