Параллельные прямые a и b пересечены прямой c в точках k и b

§ 15. Свойства параллельных прямых

(обратная теореме 14.1)

Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.

На рисунке 224 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

Пусть ∠ 1 ≠ ∠ 2. Тогда через точку K проведём прямую a 1 так, чтобы ∠ 3 = ∠ 2 (рис. 224). Углы 3 и 2 являются накрест лежащими при прямых a 1 и b и секущей c . Тогда по теореме 14.1 a 1 ‖ b . Получили, что через точку K проходят две прямые, параллельные прямой b . Это противоречит аксиоме параллельности прямых. Таким образом, наше предположение неверно, и, следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.3)

Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.

На рисунке 225 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 равны как вертикальные. Следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.2)

Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180° .

На рисунке 226 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 + ∠ 2 = 180°.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 смежные, поэтому ∠ 1 + ∠ 3 = 180°. Следовательно, ∠ 1 + ∠ 2 = 180°.

Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой ( рис. 227 ).

Докажите это следствие самостоятельно.

Задача. Докажите, что все точки одной из двух параллельных прямых равноудалены от другой прямой.

Решение. Пусть прямые a и b параллельны (рис. 228), M и N — две произвольные точки прямой a . Опустим из них перпендикуляры MK и NP на прямую b . Докажем, что MK = NP .

Рассмотрим треугольники MKN и PNK . Отрезок KN — их общая сторона. Так как MK ⊥ b и NP ⊥ b , то MK ‖ NP , а углы MKN и PNK равны как накрест лежащие при параллельных прямых MK и NP и секущей KN .

Аналогично углы MNK и PKN равны как накрест лежащие при параллельных прямых MN и KP и секущей KN . Следовательно, треугольники MKN и PNK равны по стороне и двум прилежащим углам.

Тогда MK = NP .

Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

Например, на рисунке 228 длина отрезка MK — это расстояние между параллельными прямыми a и b .

Задача. На рисунке 229 отрезок AK — биссектриса треугольника ABC , MK ‖ AC . Докажите, что треугольник AMK — равнобедренный.

Решение. Так как AK — биссектриса треугольника ABC , то ∠ MAK = ∠ KAC .

Углы KAC и MKA равны как накрест лежащие при параллельных прямых MK и AC и секущей AK . Следовательно, ∠ MAK = ∠ MKA .

Тогда треугольник AMK — равнобедренный.

1. Каким свойством обладают накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей?
2. Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей?
3. Чему равна сумма односторонних углов, образованных при пересечении двух параллельных прямых секущей?
4. Известно, что прямая перпендикулярна одной из двух параллельных прямых. Обязательно ли она перпендикулярна другой прямой?
5. Что называют расстоянием между двумя параллельными прямыми?

326. На рисунке 230 найдите угол 1.

327. На рисунке 231 найдите угол 2.

328. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.

329. Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы.

330. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:

1) один из этих углов равен 48°;

2) отношение градусных мер двух из этих углов равно 2 : 7.

331. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них на 24° меньше другого.

332. На рисунке 232 m ‖ n , p ‖ k , ∠1 = 50°. Найдите ∠ 2, ∠ 3 и ∠ 4.

333. Прямая, параллельная основанию AC равнобедренного треугольника ABC , пересекает его боковые стороны AB и BC в точках D и F соответственно. Докажите, что треугольник DBF — равнобедренный.

334. На продолжениях сторон AC и BC треугольника ABC ( AB = BC ) за точки A и B отметили соответственно точки P и K так, что PK ‖ AB . Докажите, что треугольник KPC — равнобедренный.

335. Отрезки AB и CD пересекаются в точке O , AO = BO , AC ‖ BD . Докажите, что CO = DO .

336. Отрезки MK и DE пересекаются в точке F , DK ‖ ME , DK = ME . Докажите, что ∆ MEF = ∆ DKF .

337. Ответьте на вопросы.

1) Могут ли оба односторонних угла при двух параллельных прямых и секущей быть тупыми?

2) Может ли сумма накрест лежащих углов при двух параллельных прямых и секущей быть равной 180°?

3) Могут ли быть равными односторонние углы при двух параллельных прямых и секущей?

338. На рисунке 233 AB ‖ CD , BC ‖ AD . Докажите, что BC = AD .

339. На рисунке 233 BC = AD , BC ‖ AD . Докажите, что AB ‖ CD .

340. На рисунке 234 MK ‖ EF , ME = EF , ∠ KMF = 70°. Найдите ∠ MEF .

341. Через вершину B треугольника ABC (рис. 235) провели прямую MK , параллельную прямой AC , ∠ MBA = 42°, ∠ CBK = 56°. Найдите углы треугольника ABC .

342. Прямая, проведённая через вершину A треугольника ABC параллельно его противолежащей стороне, образует со стороной AC угол, равный углу BAC . Докажите, что данный треугольник — равнобедренный.

343. На рисунке 236 ∠ MAB = 50°, ∠ ABK = 130°, ∠ ACB = 40°, CE — биссектриса угла ACD . Найдите углы треугольника ACE .

344. На рисунке 237 BE ⊥ AK , CF ⊥ AK , CK — биссектриса угла FCD , ∠ ABE = 32°. Найдите ∠ ACK .

345. На рисунке 238 BC ‖ MK , BK = KE , CK = KD . Докажите, что AD ‖ MK .

346. На рисунке 239 AB = AC , AF = FE , AB ‖ EF . Докажите, что AE ⊥ BC .

347. Треугольник ABC — равнобедренный с основанием AC . Через произвольную точку M его биссектрисы BD проведены прямые, параллельные его сторонам AB и BC и пересекающие отрезок AC в точках E и F соответственно. Докажите, что DE = DF .

348. На рисунке 240 AB ‖ DE . Докажите, что ∠ BCD = ∠ ABC + ∠ CDE .

349. На рисунке 241 AB ‖ DE , ∠ ABC = 120°, ∠ CDE = 150°. Докажите, что BC ⊥ CD .

350. Через вершину B треугольника ABC провели прямую, параллельную его биссектрисе AM . Эта прямая пересекает прямую AC в точке K . Докажите, что ∆ BAK — равнобедренный.

351. Через точку O пересечения биссектрис AE и CF треугольника ABC провели прямую, параллельную прямой AC . Эта прямая пересекает сторону AB в точке M , а сторону BC — в точке K . Докажите, что MK = AM + CK .

352. Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O . Через эту точку проведены прямые, параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно. Докажите, что периметр треугольника MOK равен длине стороны AC .

Упражнения для повторения

353. На отрезке AB отметили точку C так, что AC : BC = 2 : 1. На отрезке AC отметили точку D так, что AD : CD = 3 : 2. В каком отношении точка D делит отрезок AB ?

354. Отрезки AC и BD пересекаются в точке O , AB = BC = CD = AD . Докажите, что AC ⊥ BD .

355. В треугольнике MOE на стороне MO отметили точку A , в треугольнике TPK на стороне TP — точку B так, что MA = TB . Какова градусная мера угла BKP , если MO = TP , ∠ M = ∠ T , ∠ O = ∠ P , ∠ AEO = 17°?

Наблюдайте, рисуйте, конструируйте, фантазируйте

356. На рисунке 242 изображена очень сложная замкнутая ломаная. Она ограничивает некоторую часть плоскости (многоугольник). Как, отметив на рисунке любую точку, по возможности быстрее определить, принадлежит эта точка многоугольнику или нет?

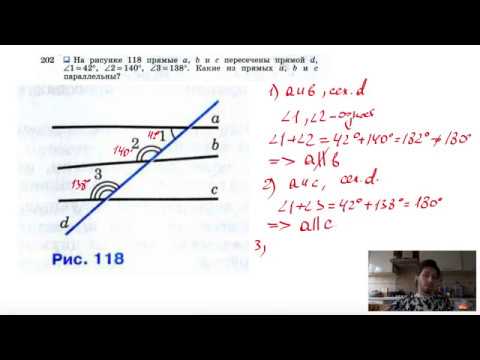
Видео:№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать

прямые a и b пересечены прямой c?

Геометрия | 5 — 9 классы

прямые a и b пересечены прямой c.

Что a||b, если угол 1 = 45 градусам, а угол 7 в три раза больше угла 3.

Подробное решение задачи.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Прямая AB и CD пересечены третьей прямой MN в точках K и Z так что точки A и C находятся в одной полуплоскости а B и D в другой относительно прямой MN?

Прямая AB и CD пересечены третьей прямой MN в точках K и Z так что точки A и C находятся в одной полуплоскости а B и D в другой относительно прямой MN.

Угол MKD = MLB углу, Докажите что прямые AB и CD параллельны.

Видео:№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

Параллельны ли прямые AB и CD если они пересечены прямой p в точках m и k причем угол BMK = 78 градусов а угол MKD в 1, 5 раза меньше угла смежного с углом BMK?

Параллельны ли прямые AB и CD если они пересечены прямой p в точках m и k причем угол BMK = 78 градусов а угол MKD в 1, 5 раза меньше угла смежного с углом BMK?

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельные прямые а и б пересечены секущей с найдите угол 1 если он в 3 раза меньше угла 2?

Параллельные прямые а и б пересечены секущей с найдите угол 1 если он в 3 раза меньше угла 2.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

На рисунке 106 прямые а и б пересечены прямой с?

На рисунке 106 прямые а и б пересечены прямой с.

Докажите, что а параллельно б, если :

1) угол 1 = 37°, угол7 = 143°

3)угол 1 = 45°, а угол 7 в три раза больше угла 3.

Видео:№198. Прямые а и b перпендикулярны к прямой р, прямая с пересекает прямую а. ПересекаетСкачать

Парралельные прямые а и b пересечены секущей с найдите угол один если он в два раза больше угла два?

Парралельные прямые а и b пересечены секущей с найдите угол один если он в два раза больше угла два.

Видео:№558. Прямые а и b пересечены параллельными прямыми АА1, BB1, CC1, причем точки А, В и ССкачать

Прямые a║b пересечены секущей С, острый угол в 3 раза меньше тупого найти эти углы?

Прямые a║b пересечены секущей С, острый угол в 3 раза меньше тупого найти эти углы.

Видео:№204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать

Параллельные прямые а и b пересечены прямой c?

Параллельные прямые а и b пересечены прямой c.

Известно, что угол 1 равен 150 градусов.

Определите угол 2.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельные прямые a и b, пересечены секущей c?

Параллельные прямые a и b, пересечены секущей c.

Угол 1 больше угла 2 на 18 градусов.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Параллельные прямые a и b, пересечены секущей c?

Параллельные прямые a и b, пересечены секущей c.

Угол 1 больше угла 2 на 154 градуса.

Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ А И С ПЕРЕСЕЧЕНЫ ПРЯМОЙ В УГОЛ 1 = 43 ГРАДУСА НАЙТИ УГОЛ 2?

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ А И С ПЕРЕСЕЧЕНЫ ПРЯМОЙ В УГОЛ 1 = 43 ГРАДУСА НАЙТИ УГОЛ 2.

СРОЧНОО 25 БАЛЛОВ.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос прямые a и b пересечены прямой c?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Угол 1 = углу 2, угол 6 = углу 3, угол 5 = углу 2 = 112 градусов. Допустим угол6 это Х, тогда угол1 это Х + 10 Тогда угол1 + угол6 + угол5 = 180 градусов. Х + 10 + х + 112 = 180 2х + 122 = 180 2х = 180 — 122 = 58 х = 58 : 2 = 29 — угол 6 и угол 3 т..

Характеристика равнин Равнина — это участок суши или дна моря, имеющий небольшое колебание высот (до 200 м) и незначительный уклон (до 5º). Они встречаются на разных высотах, в том числе и на дне океанов. Отличительная черта равнин — четкая, открыт..

Пусть большая сторона равна Х, тогда вторая сторона (Х — 10). Cos60° = 1 / 2. Сторона против угла 60° равна 14 (дано). По теореме косинусов : 14² = Х² + (Х — 10)² — 2 * Х * (Х — 10) * (1 / 2). Или 196 = Х² + (Х² — 20Х + 100) — Х² + 10Х. Х² — 10Х..

AC — 12 CB — 11 Это очень легко я давно проходила.

У равн. Треугольника боковые стороны равны значиь вторая сторона = 26см что бы найти площадь , нужно узнать высоту, для этого мы чертим высоту, она разделяет равнобедренный треуг. На два прямоугольных, сторона основания прям треуг = 20÷2 = 10см, Вы..

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

КОНТРОЛЬНАЯ РАБОТА № 3 ПО ТЕМЕ: ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Видео:№557. Стороны угла А пересечены параллельными прямыми ВС и DE, причем точки В и D лежатСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Контрольная работа № 3

Тема: Параллельность прямых и плоскостей .

1. Прямые a и b лежат в параллельных плоскостях α и β . Могут ли эти прямые быть:

Сделайте рисунок для каждого возможного случая.

2. Через точку О , лежащую между параллельными плоскостями α и β , проведены прямые l и m . Прямая l пересекает плоскости α и β в точках А ₁ и А ₂ соответственно, прямая m – в точках В ₁ и В ₂ . Найдите длину отрезка А ₂ В ₂ , если А ₁ В ₁ = 12 см, В ₁ О : ОВ ₂ = 3 : 4.

3. Изобразите параллелепипед ABCDA ₁ B ₁ C ₁ D ₁ и постройте его сечение плоскостью, проходящей через точки M , N и K , являющиеся серединами ребер АВ , ВС и DD ₁ .

Контрольная работа № 3

Тема: Параллельность прямых и плоскостей .

1. Прямые a и b лежат в пересекающихся плоскостях α и β . Могут ли эти прямые быть:

Сделайте рисунок для каждого возможного случая.

2. Через точку О , не лежащую между параллельными плоскостями α и β , проведены прямые l и m . Прямая l пересекает плоскости α и β в точках А ₁ и А ₂ соответственно, прямая m – в точках В ₁ и В ₂ . Найдите длину отрезка А ₁ В ₁ , если А ₂ В ₂ = 15 см, ОВ ₁ : ОВ ₂ = 3 : 5.

3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N , являющиеся серединами ребер DC и BC , и точку K , такую, что K DA , АK : KD = 1 : 3.

Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскость A и B в точках А1и А2 соответственно, прямая m — в точках В1 и В2. Найти длину отрезка А2В2, если А1В1 = 12см, В1О:ОВ2 = 3:4

Решение .
Через прямые А1А2 и В1В2 можно повести плоскость, которая пересечёт параллельные плоскости по параллельным прямым А1В1 и А2В2.
У образовавшихся треугольников ОА1В1 и ОА2В2 соответствующие углы равны. Углы при вершине О равны как вертикальные, а остальные — как внутренние накрест лежащие у параллельных прямых. Следовательно треугольники ОА1В1 и ОА2В2 подобны.
У подобных треугольников соответствующие стороны соотностятся через коэффициент подобия.
Откуда:
ОВ1:ОВ2 = А1В1:А2В2,
Следовательно:
А2В2 = 4 * 12 / 3 = 16

1.

2. Треугольники ОА1В1 и ОА2В2 подобны. У подобных треуг-ков отношение соответствующих сторон сохраняется и оно равно 3/5. Тогда

ОВ1/ОВ2=3/5, соответственно А1В1/А2В2=3/5, тогда

3.

Воспользуемся тем, что MN||BD и следовательно, KP||BD. находим точку P.

Или MK ∩ ABC = X, NX ∩ AB = P (метод следов). Точка P — найдена.

🎦 Видео

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Параллельные прямые. 6 класс.Скачать

№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

Параллельные прямые (задачи).Скачать

№200. На рисунке 115 AD||p и PQ||BC. Докажите, что прямая р пересекает прямые АВ, АЕ, АС, ВС и PQ.Скачать