Параллельные прямые a и b пересечены двумя параллельными прямыми ab и cd

Геометрия | 5 — 9 классы

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причем точки A и C лежат на прямо a, а точки B и D — на прямо b.

Докажите, что AC = BD.

Четырехугольник ВАСД параллелограмм по признаку пар — ма АВ параллельна СД по условию и а параллельно б по условию.

Сл — но длина АС = СД.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причём точки B и D на прямой b?

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причём точки B и D на прямой b.

Докажите AC = BD.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Сколько углов, меньших 180°, образуется, если две параллельные прямые пересечь двумя секущими?

Сколько углов, меньших 180°, образуется, если две параллельные прямые пересечь двумя секущими?

Видео:№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

Это опять я?

Не ту задачу написала.

Прошу прощения, вот она :

Прямые AB и CD пересечены секущей MN в точках K и P соответственно.

Являются ли прямые AB и CD параллельными, если угол BKP = 112° и угол KPD = 58°?

Видео:Параллельные прямые (задачи).Скачать

Прямая AB и CD пересечены третьей прямой MN в точках K и Z так что точки A и C находятся в одной полуплоскости а B и D в другой относительно прямой MN?

Прямая AB и CD пересечены третьей прямой MN в точках K и Z так что точки A и C находятся в одной полуплоскости а B и D в другой относительно прямой MN.

Угол MKD = MLB углу, Докажите что прямые AB и CD параллельны.

Видео:29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

ПОМОГИТЕ ПОЖАЛУЙСТА?

Укажите номера верных утверждений

1) если прямая a параллельна прямой с, а прямая с параллельна прямой b, то прямые а и b пересекаются

2) если при пересечении двух прямых секущей внутренние односторонние углы равны, то прямые параллельны

3) через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и притом только одну

4) если при пересечении двух прямых секущей соответственные углы равны по 60 градусов, то прямые параллельны.

Видео:№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

AB и CD — перпендикуляры к прямой BD, точки А и С лежат по разные стороны от прямой BD, Доказать что BD параллельно AD, если AB = CDС фото пожалуйста?

AB и CD — перпендикуляры к прямой BD, точки А и С лежат по разные стороны от прямой BD, Доказать что BD параллельно AD, если AB = CD

С фото пожалуйста.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Докажите , что две параллельные прямые пересечены секущей, то накрест лежащие углы равны, быстрей пожалуйста?

Докажите , что две параллельные прямые пересечены секущей, то накрест лежащие углы равны, быстрей пожалуйста.

Видео:№556. Стороны угла О пересечены параллельными прямыми АВ и CD. Докажите, что отрезки ОАСкачать

На рисунке 3 AB и CD пересекаются в их общей середине M?

На рисунке 3 AB и CD пересекаются в их общей середине M.

Через точку В проведена прямая а, параллельная прямой АD.

Докажите , что прямая а проходит через точку С.

Видео:№557. Стороны угла А пересечены параллельными прямыми ВС и DE, причем точки В и D лежатСкачать

Cколько углов , меньших 180°, образуется, если две параллельные прямые пересечь двумя секущими?

Cколько углов , меньших 180°, образуется, если две параллельные прямые пересечь двумя секущими?

Видео:Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать

Верным является высказывание под буквой :А) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны?

Верным является высказывание под буквой :

А) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Б)Если прямая пересекает одну из параллельных прямых, то она перпендикулярна другой.

В) Если две параллельные прямые пересечены секущей, то односторонние углы равны.

На этой странице находится вопрос Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причем точки A и C лежат на прямо a, а точки B и D — на прямо b?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

1. Треугольники АОК и COL равны т. К. углы AOK и COL равны как вертикальные, AO = OC по свойству параллелограмма (диагонали точкой пересечения делятся пополам), а углы AСD и ACB равны как накрест лежащие при секущей АС. Т. е. Равны по стороне и пр..

Ответ : 1176 см²Объяснение : CК — биссектриса. Свойство биссектрисы : биссектриса делит противолежащую сторону треугольника на отрезки, пропорциональные прилежащим сторонам : АВ = 30 + 40 = 70 смПо теореме Пифагора : AB² = a² + b² см см[img = 10] см..

Ну тут легко. Обозначим меньшую сторону параллелограмма за Х, а Большую за Х + 5. Теперь , площадь параллелограмма равна произведению стороны на высоту, проведенную к ней, тогда (Х + 5) * 6 = 90 Х + 5 = 15 Х = 10дм — длинна меньшей стороны тогда бо..

1) т. К треугольник равнобедренный, то у = 180 — 88 / 2, y = 46 2) 47 и 47 как накрест лежащие при параллельных прямых и секущей ab, 133 и 133 по тому же свойству (180 — 47 как развернутые) 3)149 и 149 как накрест лежащие при параллельных прямых и с..

1) в равнобедренном треугольнике углы при основании равны, значит (180 — 88) / 2 = 46 2) 133, 47(внутренние односторонние) 47, 47(накрест лежащие) 133, 133(накрест лежащие) 47, 47(соответственные) 133, 133(соответственные) 3) по принципу второй.

1 + tg²α = 1 / cos²α sin²α + cos²α = 1, cos²α = 1 — sin²α tgα = √(1 / 16). Tgα = 1 / 4. Tgα = 0, 25 ответ : tgA = 0, 25.

1)100 — 15 = 85кг проданных слив ; 85 * 80 = 6800 рублей получил ; 6800 — 6000 = 800рублей заработал.

7) тоже 30, т. К. опираются на одну дугу 8) х = (60 + 180) / 2 = 120 9) х = (180 — 70) / 2 = 55 10) х = 25 у = (360 — 100) / 2 = 130 11) х = (180 — 80) / 2 = 50 12) 1. Дуга АВ = 60, ВС = 40 и СD = 80 град 2. Х = (180 — 60) / 2 = 60.

Уголы которые вписаны в круг и упираются на точки на которые опирается другой равны.

Соотношения сторон и углов в прямоугольном треугольнике.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельные прямые a и b пересечены двумя параллельными прямыми ab и cd

Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4). Цитаты использованы в учебных целях.

Другие варианты итоговой контрольной работы в 7 классе:

Итоговая контрольная работа по геометрии
Уровень 2 (средний). Геометрия 7 класс

Вариант 3

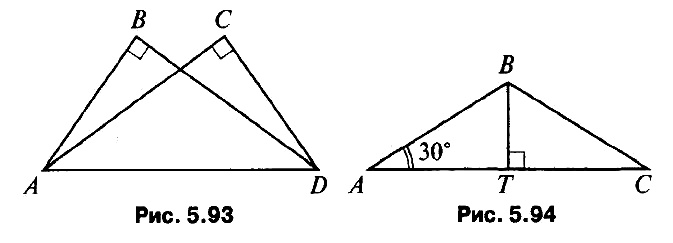
1. Дано: ∠B = ∠C = 90°, ∠ADC = 50°, ∠ADB = 40° (рис. 5.93). Доказать: ΔABD = ΔDCA.
2. В равнобедренном треугольнике угол между боковыми сторонами в три раза больше угла при основании. Найдите углы треугольника.
3. Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С лежат на прямой а, а точки В и D — на прямой b. Доказать: АС = BD.
4. * Дано: АВ = ВС, ВТ = 4 см (рис. 5.94).
   а) Между какими целыми числами заключена длина отрезка АС?
   б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.

Вариант 4

1. Дано: ∠B = ∠C = 90°, ∠ADB = 40°, ∠BDC = 10° (рис. 5.95). Доказать: ΔABD = ΔDCA.
2. В равнобедренном треугольнике угол при основании в четыре раза больше угла между боковыми сторонами. Найдите углы треугольника.
3. Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки В и D — прямой b. Доказать: АВ = CD.
4. * Дано: АВ = ВС, АС = 10 см (рис. 5.96).
   а) Между какими целыми числами заключена длина высоты AВС?
   б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.

Решения и ответы на контрольную работу:

ОТВЕТЫ на Вариант 3

№ 1. Сумма острых углов прямоугольного треугольника равна 90°.
ΔADC: ∠ACD = 90°, ∠ADC = 50°, ⇒ ∠ ACD = 90° — 50° = 40°
В прямоугольных треугольниках ABD и DCA общая гипотенуза AD и одинаковые острые углы (∠ACD = ∠ADB = 40°), ⇒ ΔABD = ΔDCA по гипотенузе и острому углу.

№ 2. В равнобедренном треугольнике углы при основании равны. А сумма углов треугольника равна 180°. Будем решать алгебраическим способом. Для удобства, назовем треугольник ABC, а бОльшим будем угол A.
Пусть угол В = х. Тогда угол С= х, а угол А равен 3х (в три раза больше). Их сумма равна х+х+3х. А по теореме суммы углов треугольника 180°. Составим уравнение: х + х + 3х = 180. Решив уравнение получим: х = 36.
Значит, угол В (при основании) равен 36°, угол С (тоже при основании) равен 36°, а угол А = 36 • 3 = 108°
Ответ: углы треугольника равны 36°, 36° и 108°.

№ 3. По условию параллельные прямые а и b пересекаются двумя параллельными секущими АВ и СD, в результате этого получается четырехугольник АВСD, в котором пары противолежащих сторон АВ и СD, АС и ВD (принадлежащие прямым а и b) параллельны, значит полученный четырехугольник АВСD является параллелограммом. Противолежащие стороны параллелограмма равны, значит АС = BD, что и требовалось доказать.

№ 4. а) между числами 13 и 14.

ОТВЕТЫ на Вариант 4

№ 1. а) ∠ADC = ∠ADB + ∠BDC = 40° + 10 °= 50°. б) ∠BAD = 180 — ∠ABD — ∠ADB = 180° — 90° — 40° = 50°. в) ∠BAD = ∠ADC = 50°; ∠ABD = ∠ACD = 90°; гипотенуза AD общая. Отсюда следует, что треугольники равны (если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны).

№ 2. Пусть ∠A и ∠С – углы при основании, а ∠В – угол между боковыми сторонами. Так как треугольник равнобедренный, то ∠A = ∠C. Угол В обозначим х, тогда ∠A = ∠C = 4х. Составим уравнение: x + 4x + 4x = 180°. Отсюда следует, что x = 20° = ∠B. Тогда ∠A = 4 • 20 = 80° = ∠C. Ответ: углы треугольника равны 80°, 80° и 20°.

№ 3. Проведем диагональ AD и докажем, что △ABD = △ACD. Так как a параллельно b, значит накрест лежащие углы равны: ∠BAD = ∠ADC и ∠BDA = ∠CAD. AD — общая, значит △ABD = △ACD по стороне и прилежащим углам. Следовательно, AB = CD

№ 4. a) Между числами 8 и 9.

Информация для учителя:

По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

Другие варианты итоговой контрольной работы в 7 классе:

Вы смотрели: Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4).

В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

🔥 Видео

Пары углов в геометрииСкачать

№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

№204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать

Параллельные прямые. 6 класс.Скачать

№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать

Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Теоремы об углах, образованных двумя параллельными прямыми и секущей.Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать