Отрицательный угол в треугольнике

Сумма двух углов. На координатной плоскости $Oxу$ рассмотрим окружность единичного радиуса с центром в начале координат (рис.). Пусть произвольный угол $alpha$ (на чертеже положительный) получен в результате вращения некоторото подвижного радиуса-вектора от его начального положения $bar$, совпадающего с положительным направлением оси $Ox$, до его конечного положения $bar$. Примем теперь положение радиуса-вектора $bar$ за начальное и отложим от него произвольный угол $beta$ (на чертеже положительный), который получим в результате вращения некоторого подвижного радиуса-вектора от его начального положения $bar$ до его конечного положения $bar$. В результате этих действий мы получим угол, который будем называть суммой углов $alpha$ и $beta$. (Начальное положение подвижного радиуса-вектора $bar$, конечное положение радиуса-вектора $bar $.)

Разность двух углов.

Под разностью двух углов $alpha$ и $beta$, которую обозначим $alpha — beta$, мы будем понимать такой третий угол $gamma$, который в сумме с углом $beta$ дает угол $alpha$, т. е. $gamma = alpha — beta$, если $beta + gamma = alpha$. Разность двух углов $alpha$ и $beta$ можно трактовать как сумму углов $alpha$ и $- beta$. В самом деле, $[alpha + (- beta)] + beta = alpha$ (рис.). Вообще, для любых углов их сумма измеряется алгебраической суммой действительных чисел, измеряющих эти углы.

Пример 3. Угол $beta = +780^$, а угол $beta^ = -1110^$. Сумма их $beta + beta^ = 780^ + (- 1110^) = -330^$.

В формуле (1) раздела «Углы и дуги, большие $360^$» предполагалось, что $n$ — любое целое неотрицательное число. Если же предположить, что $n$ — любое целое число (положительное, отрицательное или нуль), то при помощи формулы

где $0^ leq alpha < 360^, n = 0, pm 1, pm 2, cdots$ можно будет записать любой угол, как положительный, так и отрицательный.

Пример 4. Угол, равный $-1370^$, можно записать так:

Здесь $n = -4, alpha = + 70^$.

Заметим, что все углы $beta_$, записанные при помощи формулы (1), при разных значениях $n$, но одном и том же $alpha$, имеют общие начальную ($bar $) и конечную ($bar$) стороны (рис.). Поэтому построение любого угла $beta_$ сводится к построению соответствующего неотрицательного угла $alpha$ меньшего $360^$. На рис. углы $beta_ = alpha + 360^ n$ между собой не отличаются, они различаются лишь процессом вращения радиуса-вектора, который привел к их образованию.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Измерение углов

Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.

На картинке видны 4 разных угла, образованных пересечением прямых AB и CD

Обычно углы измеряются в градусах, что обозначается как °. Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°). Таким образом, градус — это $frac$ круга.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Углы больше 360 градусов

Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.

Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.

Пример 2
1. Найти количество кругов, описанных объектом, образующем угол
a) 380°
b) 770°
c) 1000°
Решение
a) 380 = (1 × 360) + 20
Объект описал один круг и 20°
Так как $20^ = frac = frac$ круга
Объект описал $1frac$ кругов.

b) 2 × 360 = 720
770 = (2 × 360) + 50
Объект описал два круга и 50°
$50^ = frac = frac$ круга
Объект описал $2frac$ круга
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^ = frac = frac$ кругов
Объект описал $2frac$ кругов

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Положительные и отрицательные углы

Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.

В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.

Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)

Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360. Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.

Пример 3
1. Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°

2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°

2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Радиан

Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. Это единица измерения угловой величины. Такой угол примерно равен 57,3°.
В большинстве случаев, это обозначается как рад.
Таким образом $1 рад approx 57,3^$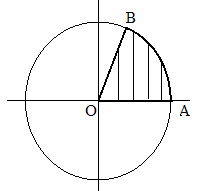

Радиус = r = OA = OB = AB
Угол BOA равен одному радиану

Поскольку длина окружности задается как $2pi r$, то в окружности $2pi$ радиусов, а значит в целом круге $2pi$ радиан.

Радианы обычно выражаются через $pi$ во избежание десятичных частей в вычислениях. В большинстве книг, аббревиатура рад (rad) не встречается, но читатель должен знать, что, когда речь идет об угле, то он задан через $pi$, а единицами измерения автоматически становятся радианы.

Пример 4
1. Преобразовать 240°, 45°, 270°, 750° и 390° в радианы через $pi$.
Решение
Умножим углы на $frac$.

2. Преобразовать следующие углы в градусы.
a) $fracpi$
b) $3,12pi$
c) 2,4 радиан
Решение
$180^ = pi$
a) $frac pi = frac times 180 = 225^$
b) $3,12pi = 3,12 times 180 = 561,6^$
c) 1 рад = 57,3°
$2,4 = frac = 137,52$

Отрицаетльные углы и углы больше, чем $2pi$ радиан

Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2pi$.

Пример 5
1. Преобразовать $-fracpi$ и $-fracpi$ в позитивные углы в радианах.

Решение
Прибавляем к углу $2pi$
$-fracpi = -fracpi + 2pi = fracpi = 1fracpi$

Когда объект вращается на угол больший, чем $2pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2pi$, результат равен или меньше, но как можно ближе к данному числу.

Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10pi$
b) $9pi$
c) $fracpi$

Решение
a) $-10pi = 5(-2pi)$;
$-2pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.

b) $9pi = 4(2pi) + pi$, $pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки

c) $fracpi=3,5pi=2pi+1,5pi$, $1,5pi$ равно три четверти цикла $(frac=frac)$
объект прошел один и три четверти цикла против часовой стрелки

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

• Синус угла – отношение противолежащего катета к гипотенузе;
• Косинус угла – отношение прилежащего катета к гипотенузе;
• Тангенс угла – отношение противолежащего катета к прилежащему;
• Котангенс угла – отношение прилежащего катета к противолежащему.

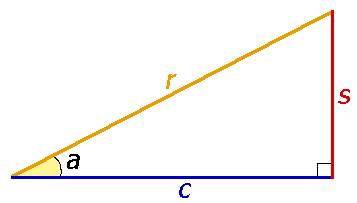
Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

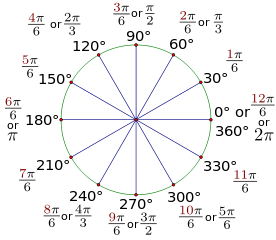
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

0°	30°	45°	60°	90°
sin	0	1	√3	–
ctg	–	√3	1	Принцип повтора знаков тригонометрических функций Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Видео:Синус, косинус произвольного угла. 9 класс.Скачать Тригонометрический круг Углы в радианах Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. 🔍 Видео Внешний угол треугольникаСкачать ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать СИНУС И КОСИНУС ЛЮБЫХ УГЛОВ | ТригонометрияСкачать Найдите угол: задача по геометрииСкачать №592. Постройте угол а, если:Скачать ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать Углы треугольникаСкачать 7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать Площади треугольников с равным углом.Скачать Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать Отрицательный аргумент у тригонометрических функций [понять нельзя заучивать]Скачать ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать Поделиться или сохранить к себе: Смотрите также Площадь равнобедренного треугольника Площадь прямоугольного треугольника Плечо силы в треугольнике Плетение треугольника мозаичным плетением Плетение треугольника из лозы Плетение треугольника из веревки Плетение из газетных трубочек треугольник Плетение из бисера треугольник