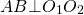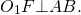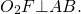Отрезок соединяющий центры двух пересекающихся окружностей делится их общей

Геометрия | 5 — 9 классы

Докажите, что если две окружности имеют общую хорду, то прямая проходящая через центры окружности делят общую хорду пополам.

Все точки, равноудаленные от концов отрезка, лежат на перпендикуляре, проведенном через середину этого отрезка.

В случае этой хорды линия центров в 2 точках (в центрах окружностей) совпадает с этим перпендикуляром (ну, концы хорды лежат на окружностях, значит, они равноудалены от центров), а, значит, — совпадает везде (это одна из аксиом геометрии).

Поэтому линия центров двух окружностей, имеющих общую хорду, перпендикулярна этой общей хорде и делит её пополам.

Видео:Геометрия Общая хорда двух окружностей служит для одной из них стороной вписанного квадрата, а дляСкачать

Две окружности имеют общий центр?

Две окружности имеют общий центр.

Докажите, что хорды большей окружности, касающиеся меньшей окружности, равны между собой.

Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

ПОМОГИТЕ, ПРОШУ?

Докажите, что прямая, проходящая через две точки пересечения двух окружностей, делит пополам отрезок, соединяющий точки касания этих окружностей с их общей касательной.

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду?

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Докажите если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, перпендикулярна данной хорде?

Докажите если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, перпендикулярна данной хорде.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Радиус ОМ окружности с центром О делит хорду АВ пополам?

Радиус ОМ окружности с центром О делит хорду АВ пополам.

Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Докажите, что если две окружности имеют общую хорду, то прямая,проходящая через центры этих окружностей, перпендикулярна даннойхорде?

Докажите, что если две окружности имеют общую хорду, то прямая,

проходящая через центры этих окружностей, перпендикулярна данной

Видео:Алгоритмы. Пересечение окружностейСкачать

Две окружности с равными радиусами пересекаются в двух точках?

Две окружности с равными радиусами пересекаются в двух точках.

Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам?

Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам.

Видео:№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Прямая l касается в точке M окружности с центром О?

Прямая l касается в точке M окружности с центром О.

Хорда AB параллельна l.

Доказать, что прямая OM делит хорду AB пополам.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополамПОМОГИТЕ?

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополам

Вы перешли к вопросу Помогите пожалуйста?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Катет лежащийи протов угла в 30° равен половине гипотенузы.

Линейка, рулетка, сантиметр.

Кроме обычных линейки, рулетки, сантиметра, можно ещё вспомнить штангенциркуль для точного измерения небольших расстояний. С помощью теодолита можно определить достаточно точно расстояние до предмета в пределах 50 — 300 метров.

Ac = √(100 — 81) = 3 x = √(9 + 324) = √333 = 3√37.

Видео:Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Общая хорда двух окружностей

Общая хорда двух пересекающихся окружностей перпендикулярна прямой, проходящей через центры этих окружностей.

Дано : окр. (O1; R) ∩ окр. (O2; r)=A, B.

Соединим центры окружностей с точками A и B. Обозначим точку пересечения прямой O1O2 с хордой AB как F.

Рассмотрим треугольники O1AO2 и O1BO2.

3) O1O2 — общая сторона.

Из равенства треугольников следует равенство соответствующих углов: ∠AO1F=BO1F, то есть O1F- биссектриса угла AO1B.

Треугольник AO1B — равнобедренный с основанием AB (O1A=O1B=R). Следовательно, биссектриса O1F является также его высотой и медианой. Таким образом,

Аналогично доказывается, что

По теореме о существовании и единственности прямой, перпендикулярной данной,через точку F можно провести только одну прямую, перпендикулярную данной прямой AB.

Следовательно, центры окружностей O1, O2 и точка F лежат на одной прямой O1O2, а общая хорда окружностей перпендикулярна этой прямой:

Видео:1 2 4 сопряжение окружностейСкачать

Презентация по теме «Полезные факты планиметрии»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Полезные факты из планиметрии Лучше это знать… <

Биссектрисы смежных углов перпендикулярны. Биссектрисы внутренних односторонних углов при двух параллельных прямых и секущей перпендикулярны.

а) Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный. б) Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Если М — точка касания со стороной АС и N-точка касания со стороной АВ окружности, вписанной в треугольник ABC, то AM = AN = р — ВС, где р — полупериметр треугольника.

Если окружность касается основания ВС треугольника ABC и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника ABC.

Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника ABC лежит на окружности S.

Если прямая, проходящая через точку А и центр О вписанной окружности треугольника ABC, вторично пересекает описанную окружность треугольника в точке М, то треугольники ВОМ и СОМ равнобедренные.

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований трапеции, равен их полуразности.

Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.

Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.

Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна её средней линии.

Замечательное свойство трапеции. а) Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

Отрезок прямой, параллельной основаниям трапеции, заключённый внутри трапеции, разбивается её диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны.

Площадь четырёхугольника с перпендикулярными диагоналями равна половине произведения диагоналей.

Площадь любого четырёхугольника равна половине произведения диагоналей на синус угла между ними.

Середины двух противоположных сторон любого четырёхугольника и середины его диагоналей либо являются вершинами параллелограмма, либо лежат на одной прямой.

а) Диаметр, перпендикулярный хорде, делит её пополам. б) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде. в) Серединный перпендикуляр к хорде проходит через центр окружности. АВ-диаметр окружности, CD-хорда, М-середина хорды CD

Как это работает…

Геометрическое место точек, из которых отрезок АВ виден под данным углом, есть две дуги равных окружностей с общей хордой АВ, лежащие по разные стороны от прямой АВ, без точек А и В.

а) Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде и делит её пополам. б) Линия центров двух касающихся окружностей проходит через точку касания.

Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.

Общие хорды (или их продолжения) трёх попарно пересекающихся окружностей проходят через одну точку либо параллельны.

Две окружности касаются внутренним образом в точке М. Если АВ — хорда большей окружности, касающаяся меньшей окружности в точке Т, то МТ — биссектриса угла АМВ.

Как это работает… Если точки C и D расположены по одну сторону от отрезка АВ и отрезок виден из этих точек под одинаковым углом, то А, В, С и D лежат на одной окружности

Если из точек C и D отрезок АВ виден под прямым углом, то А, В, С и D лежат на одной окружности, центр которой – середина АВ. Как это работает, смотрим в следующей задаче:

Как это работает, смотрим в следующих задачах:

Как это работает, смотрим в следующей задаче:

Как это работает, смотрим в следующей задаче:

Как это работает… Медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2 : 1, считая от вершины.

Как это работает…

Если H точка пересечения высот треугольника ABC, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. Как это доказать…

Точки О, H и точка М пересечения медиан треугольника ABC лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ: МН = 1:2.

Точки, симметричные точке пересечения высот (ортоцентру) треугольника ABC относительно прямых АВ, АС и ВС, лежат на описанной окружности треугольника ABC.

Точки, симметричные точке пересечения высот треугольника ABC относительно середин его сторон, лежат на описанной окружности треугольника ABC.

Если АК, ВМ и CN — высоты остроугольного треугольника ABC, то биссектрисы треугольника KMN (ортотреугольника треугольника ABC) лежат на прямых АК, ВМ и CN.

Если же треугольник ABC тупоугольный, то на этих прямых лежат биссектрисы двух внешних и третьего внутреннего углов треугольника KMN.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 987 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия 7 класса в одной задаче. Геометрия 7 класс кратко | МатематикаСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 536 388 материалов в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Глава 8. Некоторые сведения из планиметрии

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 23.08.2017
• 6065
• 208

• 23.08.2017
• 329
• 3

• 23.08.2017
• 291
• 0

• 23.08.2017
• 495
• 0

• 23.08.2017
• 553
• 2

• 22.08.2017
• 2567
• 3

• 22.08.2017
• 358
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 23.08.2017 5540
• PPTX 1.5 мбайт
• 116 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Гайкова Лариса Иннокентьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 5 месяцев
• Подписчики: 0
• Всего просмотров: 56175
• Всего материалов: 50

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Школьники Ленобласти уйдут на внеплановые каникулы

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Минобрнауки учредит стипендию для студентов — победителей международных олимпиад

Время чтения: 1 минута

Володин призвал выработать единые нормы организации групп продленного дня

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎦 Видео

Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Задача №16. Пересекающиеся и касающиеся окружности.Скачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...Скачать