Отрезок ав является хордой окружности с центром о найдите угол

Условие

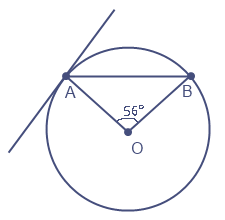
Отрезок AB является хордой окружности с центром О. Найдите угол между прямой AB и касательной к окружности, проходящей через точку А, если угол AOB равен 56°. Ответ дайте в градусах.

Решение

[r][b]Теорема:[/b] Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой[/r]

Центральный угол AOB равен дуге на которую он опирается, то есть дуга AB равна углу AOB = 56.

Из нашей теоремы следует, что угол между касательной и хордой AB равен половине дуги AB, то есть 56/2 = 28

Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

Отрезок АВ является хордой окружности с центром О?

Геометрия | 10 — 11 классы

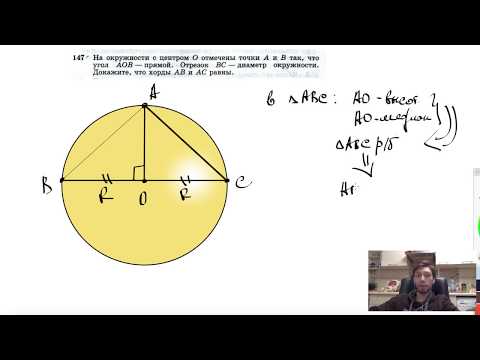
Отрезок АВ является хордой окружности с центром О.

Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 56 градусов.

Ответ дайте в градусах.

Получается равнобедренный треугольник АВО гду угол АОВ = 56

значит угол ОАВ и АВО равны.

= (180 — 56) / 2 = 62 градуса

В точке касания касательной угол 90 градусов

чтобы найти угол между касательной и прямой АВ отнимем от 90 угол ОАВ

угол х = 90 — 62 = 28 градусов.

Решается довольно просто, вот решение :

Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Отрезок прямой АВ — хорда, окружности с центром в точке О?

Отрезок прямой АВ — хорда, окружности с центром в точке О.

Угол АОВ равен 146 гр.

Найдите величину угла между прямой и касательной к окружности, проходящей через точку А.

Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

Прямая касается окружности в точке К ?

Прямая касается окружности в точке К .

Точка О центр окружности.

Хорда КМ образует с касательной угол равный 30 градусов.

Найдите велечину угла ОМК.

Ответ дайте в градуса.

Видео:№641. Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенными изСкачать

Отрезок AB является хордой к окружности с центром O?

Отрезок AB является хордой к окружности с центром O.

Найдите угол между прямой AB и касательной к окружности, проходящей через точку A, если угол AOB равен 56.

Видео:Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Касательные в точках А и В к окружности с центром О пересекаются под углом 56 градусов ?

Касательные в точках А и В к окружности с центром О пересекаются под углом 56 градусов .

Найдите угол АОВ ответ дайте в градусах.

Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Прямая касается окружности в точке К ?

Прямая касается окружности в точке К .

Точка О — центр окружности хорда КМ образует с касательной, угол равный 4град.

Найдите величину угла ОМК .

Ответ дайте в градусах.

Видео:№ 145 - Геометрия 7-9 класс АтанасянСкачать

Прямая касается окружности в точке К?

Прямая касается окружности в точке К.

Точка О — центр окружности.

Хорда КМ образует с касательной угол, равный 60 (градусов) .

Найдите величину угла ОМК .

Ответ дайте градусах.

Видео:2175 AC и BD диаметры окружности с центром О угол acb равен 35 Найдите угол aodСкачать

Касательные и окружности с центром О в точках А и В пересекаются под углом 72°?

Касательные и окружности с центром О в точках А и В пересекаются под углом 72°.

Найдите угол АОВ .

Ответ дайте в градусах.

Видео:№643. Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, еслиСкачать

Хорда АВ стягивает дугу в окружности в 75°?

Хорда АВ стягивает дугу в окружности в 75°.

Касательные к окружности, проведенные в точках А и В, пересекаются в точке О.

Найдите угол АОВ.

Ответ дайте в градусах.

Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Прямая касается окружности в точке K?

Прямая касается окружности в точке K.

Точка 0 — центр окружности.

Хорда KM образует с касательной угол, равный 40 градусов.

Найдите величину ОМК.

Ответ дайте в градусах.

Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Прямая касается окружности в точке К?

Прямая касается окружности в точке К.

Точка О — центр окружности.

Хорда КМ образует с касательной угол, равный 40°.

Найдите величину угла ОМК.

Ответ дайте в градусах.

На этой странице вы найдете ответ на вопрос Отрезок АВ является хордой окружности с центром О?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Ответ : 14Пошаговое объяснение : CD = BD — BCCD = 27 + x — (3x + 47) = 27 + x — 3x — 47 = — 2x — 20CE = CD + DE = — 2x — 20 + 10 = — 2x — 10С другой стороны, СЕ = х + 26, x + 26 = — 2x — 103x = — 36x = — 12CE = x + 26 = — 12 + 26 = 14.

Решение в приложении.

ЕН⊥СН и EF⊥CF. Углы между соответственно перпендикулярными прямыми равны, значит∠FCH = ∠FEH. ВЕ = CF, значит ЕBCF — прямоугольник. BF — диагональ. Точка О — центр описанной окружности около прямоугольника. ∠FCH = ∠FEH значит FH — хорда окружност..

По теореме Пифагора 100 — 73 = 27. Сторона треугольника равна 2 корень из 27, или 6 корень из 3. Треугольник равносторонний. Расстояние от данной точки до плоскости треугольника — расстояние от точки до точки пересечения биссектрис (высот, медиан)..

16 — (5×2) = 6 6÷2 = 3 Друга сторона паралелограма 3см.

Sтрап. = ½(17 + 9)×4 = 13×4 = 52см².

12) С 16) А 17) D 18) С.

180 — 90 — 70 = 20 180 — (20 * 2) = 140 — один угол 180 — 140 = 40 — другой угол.

4, 2 / 6 = 0, 7 — будет равны две части, поделенные в серединке. 4, 2 — 0, 7 = 3, 5.

Значит угол B = углуD = 120 как противоположные в параллелограмме угол D находится между сторонами AD и DC значит можно воспользоваться формулою площади S = AD * DC * sinD = 12 * 32 / кор3 * кор3 / 2 = 192 см ^ 2 что такое кор3 / 2 это синус120.

Видео:Задача 6 №27877 ЕГЭ по математике. Урок 118Скачать

Подготовка к ОГЭ. Окружность.
презентация к уроку по геометрии (8, 9 класс) на тему

Презентация РР. В презентации рассмотрены решения задач первой части по теме «Окружность».

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Скачать:

Предварительный просмотр:

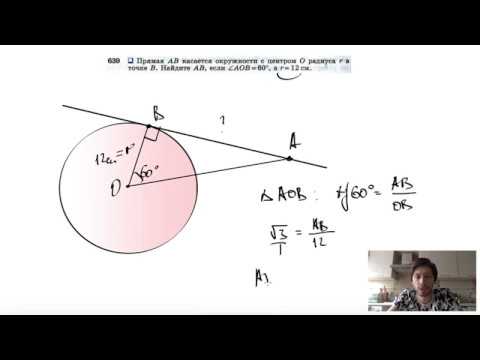
Видео:№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

Подписи к слайдам:

Подготовка к ОГЭ. Окружность.

Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если МВ = 8 см, МС = 6 см, М D = 4 см. А В С D M A М ∙ МВ = СМ ∙ MD 8 4 6 A М ∙ 8 = 6 ∙ 4 A М = 3

Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 147. А С В 0 Сумма углов четырехугольника — 360 Радиусы, проведенные в точку касания – перпендикулярны касательной. ВАС = 360 – 90 – 90 – 147 = 33

Точки А и В делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на меньшую из дуг. А В 5х 7х 0 5х + 7х = 360 х = 30 АОВ = 5 ∙ 30 = 150

Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см. А В С 1 8 15 0 Т.к. ОС АВ, то АС=ВС=9 по т. Пифагора ОС =

Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 28. А В С 28 0 ОА АС ( как радиус, проведенный в точку касания ) — равнобедренный ( ОА=ОВ – как радиусы одной окружности )

Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол ОСВ равен 39. А В 39 0 С — равнобедренный ( ОС=ОВ – как радиусы одной окружности ) или Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см. А В С М К Р 4 3 6 Отрезки касательных, проведенных из одной точки равны. ВМ = ВК АМ = АР СР = СК 6 3 4 АВ = 10 АС = 7 ВС = 9 Р = 10 + 7 + 9 = 26

Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см. А В С Центр описанной около п /у треугольника окружности лежит на середине гипотенузы. d = AC sinA =3/7 15 sinA = ВС/АС 3/7 = 15/АС АС = 35

Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120, а расстояние от центра окружности до вершины этого угла равно 18 см. 0 Т.к. в вписанном треугольнике тупой угол, то этот треугольник лежит по одну сторону от центра окружности. А В С 120 ОВ = r = 18

Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см. 0 А В 20 С 24 Т.к. ОК АС, то АК=КС=10 К по т. Пифагора ОС =

Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD , если АВ = 10 см, а расстояния от центра окружности до хорд АВ и CD равны соответственно 12 см и 5 см. А В X 1 2 5 0 C D 10 Y АХ = 5 по т. Пифагора ОА = ОА = ОС = 13 по т. Пифагора С Y = CD = 24

Отрезки АВ и BC являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен 42. А В 42 0 С АСВ – вписанный угол, АОВ – соответствующий ему центральный АОВ = 180 – 42∙2=96 АОВ= 96 : 2 = 48

В окружность вписан четырехугольник АВС D . Найдите угол АС D , если углы BAD и ADB равны соответственно 73 и 37. А В 37 С D 73 ABD : ABD = 180 – (73 + 37) = 70 АВ D = ACD – как вписанные углы, опирающиеся на одну дугу A С D = 70

Окружность с центром О касается сторон угла с вершиной А, величина которого равна 40, в точках В и С. Найдите углы треугольника ВОС. А С В 0 АОВ – п /у (радиус, проведенный в точку касания, перпендикулярен касательной) АОВ = АОС по катету и гипотенузе (АО – общая, ОВ = ОС = r ) ОАВ = 20 ВОА= 70 ВОС = 140 ОВС = ОСВ = (180 – 140) : 2 = 20

Отрезки АВ и АС являются хордами окружности с центром О. Найдите угол ВАС, если известно, что он является острым и что углы АВО и АСО равны соответственно 23 и 32. А В 23 0 С 32 Угол ВАС – острый, значит его стороны лежат по разные стороны от центра окружности. — равнобедренный — равнобедренный ОАВ = 23 ОАС = 32 ВАС = 23 + 32 = 55

Радиус окружности, описанной около равнобедренного треугольника равен 5 см, а высота, проведенная к основанию, равна 8 см. Найдите площадь треугольника. 0 А В С 5 8 Н Т.к. треугольник р /б, то центр описанной окружности лежите на высоте, проведенной к основанию. ОА = ОВ = R = 5 ОН = 8 – 5 = 3 по т. Пифагора АН = АС = 8 S = ½ ∙ 8 ∙ 8 = 32

Найдите площадь п /у трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность. 10 16 Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны. А В С D АВ + CD = ВС + AD = 26 Т.к. трапеция – п /у, то АВ = h S = 130

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см. 5 А В D С Т.к. в параллелограмм можно вписать окружность, он является ромбом. Р = 4а Р = 4 ∙ 5 = 20

В трапецию, сумма длин боковых сторон которой равна 16 см, вписана окружность. Найдите среднюю линию трапеции. Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны. В С D АВ + CD = ВС + AD = 16 К L = 8 А К L

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

По теме: методические разработки, презентации и конспекты

Подготовка к ГИА. Окружность.Центральные и вписанные углы.

Презентация по теме «Окружность.Центральные и вписанные углы» . Материал содержит повторение вопросов теории и задачи для подготовки к ГИА по этой теме.

Презентация к окружному семинару учителей английского языка «Методика подготовки к сдаче ЕГЭ по английскому языку (Письмо часть С2 Эссе)

Подробные поэтапные рекомендации по выполнению части С2 (написание эссе).

6 класс. Задания для подготовки к проверочным работа по теме «Пропорции. Длина окружности и площадь круга»

Материал предназначен для родителей для того, чтобы они могли проконтролировать подготовку детей к различным проверочным работам.

Памятка для подготовки ГИА «Окружность»

Памятка ученикам по теме » Окружность».

Углы,связанные с окружностью. Подготовка к ГИА

Повторяются вписанные и центральные углы, их градусные меры.

Решение задач по теме: «Движение по окружности» Подготовка к ЕГЭ задание «В»

Решение задач по теме «Движение по окружности».

Благодарность за подготовку учащегося к окружному этапу городского конкурса «Ученик года»

Представлена БЛАГОДАРНОСТЬ за подготовку учащегося к окружному этапу городского конкурса «Ученик года -2013».

🎬 Видео

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

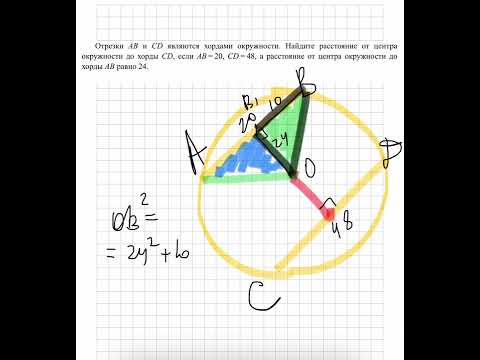
№651. Хорды АВ и CD окружности с центром О равны, а) Докажите, что две дуги с концами А и ВСкачать

Отрезок AB=40 касается окружности радиуса 75 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать