Отрезки стягивающие равные дуги окружности

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Равные хорды

Выясним, какими свойствами обладают равные хорды и равные дуги.

Равные хорды равноудалены от центра окружности.

Дано : окр. (O;R), AB и CD — хорды,

Соединим центр окружности с концами хорд.

I. Рассмотрим треугольники AOB и COD.

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.

II. Рассмотрим прямоугольные треугольники AOF и COK.

2) ∠A=∠C (по доказанному).

Из равенства треугольников следует равенство соответствующих сторон: OF=OK.

Что и требовалось доказать .

Если хорды равноудалены от центра окружности, то они равны.

Дано: окр. (O;R), AB и CD — хорды,

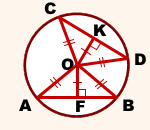
Соединим центр окружности с концами хорд.

I. Рассмотрим прямоугольные треугольники OKD и OFB.

1)OF=OK (по условию)

2)OD=OB (как радиусы).

Из равенства треугольников следует равенство соответствующих сторон:

II. Рассмотрим треугольники AOB и COD.

Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.

По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.

Что и требовалось доказать.

Равные хорды стягивают равные дуги.

Дано : окр. (O;R), AB и CD — хорды, AB=CD,

Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.

Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD

Что и требовалось доказать .

Хорды, стягивающие равны дуги, равны.

Дано: окр. (O;R), AB и CD — хорды,

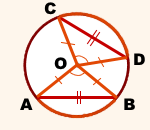
Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.

Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.

Из равенства треугольников следует равенство соответствующих сторон: AB=CD.

Отрезки стягивающие равные дуги окружности

ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.

§ 71. ЗАВИСИМОСТЬ МЕЖДУ ХОРДАМИ И ДУГАМИ.

Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.

При этом будем иметь в виду дуги, меньшие полуокружности.

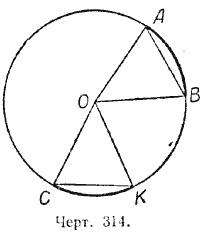
Теорема 1. Равные дуги стя гиваются равными хордами.

Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК (черт. 314).

Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.

Теорема 2 (обратная). Равные хорды стягивают равные дуги.

Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (черт. 314).

Доказательство. Соединим концы хорд с центром окружности— точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: АВ = СК.

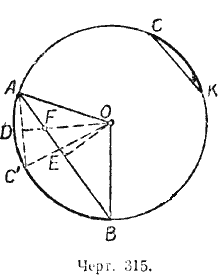
Теорема 3. Большая дуга стягивается и большей хордой.

Пусть дуга АВ больше дуги СК (черт. 315).

Требуется доказать, что хорда АВ больше хорды СК.

Доказательство. Передвинем по окружности дугу СК так, чтобы точка К совместилась с точкой А, тогда точка С займёт положение С’ на дуге АВ между точками A и В, дуга СК примет положение дуги АС’, а хорда СК примет положение хорды АС’. Проведём радиусы в точки A, В и С’. Опустим из центра О перпендикуляры ОЕ и ОD на хорды АВ и АС’. В треугольнике ОFE отрезок ОЕ — катет , а отрезок ОF — гипотенуза, поэтому OF > ОЕ, а потому и OD > OE.

Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора (§ 58) катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС’, значит, и хорда АВ больше хорды АС’. Вследствие равенства хорд АС’ и СК получаем
АВ > СК.

Теорема 4 (обратная). Большая хорда стягивает и большую дугу.

Пусть хорда А В больше хорды СК.

Требуется доказать, что дуга АВ больше дуги СК (черт. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:

АВ СК.

Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.

Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, АВ > СК.

💥 Видео