Видео:Конформные отображения c помощью дробно-линейной функции: отображение по трем точкамСкачать

Конформные отображения. Дробно-линейная функция
Определение 1. Функция вида
где a, b, c, d – комплексные числа, называется дробно-линейной.
Отображение, задаваемое этой функцией, называется дробно- линейным.
Условие ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная
Для 0 c ≠ предполагаем, что
для c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция
является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.
Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.
Дробно-линейные отображения переводят:
1) окружность или прямую в окружность или прямую (круговое свойство);
2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь «окружность», в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.
Существует единственное дробно-линейное отображение, которое три разных точки z1, z2, z3 переводит соответственно в три разные точки w1, w2, w3. Это отображение задается формулой
Если одна из точек zk или wk (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит zk или wk, требуется заменить единицами.
Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.
Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:
1) заданная точка z0 ∈ D отображается в заданную точку w0 ∈ D’, а любая кривая, выходящая из точки z0, поворачивается на заданный угол α w0 = f (z0), α = arg(f ‘(z0));
2) точки z0 ∈ D и z1 ∈ γ отображаются соответственно в заданные точки w0 ∈ D’ и w1 ∈ Γ.
Пример 1. Найти образ окружности, заданной уравнением
x 2 + y 2 + 2x − 4y + 1 = 0,
при отображении w = 1/z.
Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности x 2 + y 2 + 2x − 4y + 1 = 0, выберем три точки, например: z1 = −1 z2 = 1 + 2i, z3 = −3 + 2i, образами которых при отображении w = 1/z будут точки
Точками w1, w2, w3 однозначно определяется образ данной окружности, уравнение которой:
Для отображения w = 1/z имеем
Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).
Пример 2. Найти образ области D при отображении 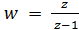
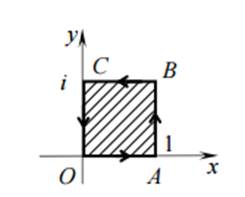
Будем искать образ границы области D (рис. 1).
Сторона OA: y = 0, 0 ≤ x ≤ 1 отображается на отрицательную часть действительной оси (v = 0, − ∞
Рис. 1. Область D
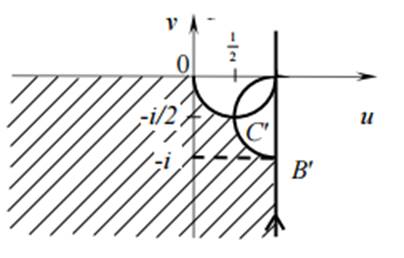
Рис. 2. Образ области D
Сторона AB: x = 1, 0
Сторона BC: y =1, 1 ≥ x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид
Исключив параметр x, получим
Аналогично образ стороны CO определяется уравнением
В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 1.
Пример 3. Найти дробно-линейное отображение, которое точки z1 = 1 и z2 = −1 оставляет неподвижными, а точку z3 = i переводит в точку w3 = 0.
Найти образ полуплоскости Im(z) > 0 при данном отображении.
Решение. По условию имеем три пары соответствующих точек
Применяя формулу (2), получим искомое дробно-линейное отображение 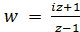
Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: z1 =1, z2 = 0, z3 = −1, образами которых бу- дут точки w1 = 1, w2 = −i, w3 = −1. Они лежат на окружности |w| =1. По принципу соответствия границ получаем, что образом верхней полуплоскости будет область D’= <w, |w|
Пример 4. Найти дробно-линейное отображение, которое круг |z − 4i| u так, что w(4i) = −4, w(2i) = 0.
Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки z1 = 4i и z3 = ∞, симметричные относительно окружности |z − 4i| = 2, перейдут в точки w1 = −4 и w3 = − 4i, симметричные относительно прямой u = v . Таким образом, найдена третья пара точек z3 = ∞ и w3 = −4i. По формуле (2) найдем искомое отображение 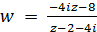
Видео:Конформные отображения c помощью дробно-линейной функции: круговое свойствоСкачать

Сохранение симметрии при дробно-линейном отображении.
Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку , которая переходит в бесконечно удаленную точку. Если окружность не проходит через точку , то при указанном дробно-линейном отображении перейдет в окружность. Аналогичным образом преобразуются и прямые: прямая при отображении переходит в прямую, если проходит через точку . Иначе переходит в окружность.
Определение 5. Точки и называют симметричными относительно окружности в , если они лежат на одном луче, выходящем из центра окружности , и произведение их расстояний до центра окружности равно квадрату радиуса окружности, т.е. и .
Так как для точек и , симметричных относительно окружности , верно соотношение , то равно действительному положительному числу. А поскольку, согласно определению,
Так как при приближении точки к центру окружности симметричная ей точка стремится к бесконечно удаленной точке, то центр окружности и бесконечности удаленную точку естественно считать симметричными относительно окружности .
Теорема 11. Произвольное дробно-линейное отображение преобразует любые точки и , симметричные относительно окружности на , в точки и , симметричные относительно образа этой окружности.
Рассмотрим семейство всех окружностей на , проходящих через и . Каждая из этих окружностей перпендикулярна . Дробно-линейное отображение переводит каждую окружность в окружность в , перпендикулярную (в силу теоремы : Функция с дополнением и осуществляет взаимно однозначное и непрерывное отображение расширенной комплексной плоскости на расширенную коплексную плоскость ) образу окружности . Согласно критерию симметричности точек, получаем, что точки и , через которые проходят все окружности семейства , симметричны относительно окружности .
Видео:Дробно Линейное Преобразование | Конформные отображенияСкачать

Дробно-линейные отображения


Дробно-линейной функцией называется функция вида: 


Перечислим без доказательства свойства дробно-линейной функции.
- Дробно-линейная функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя. При этом точка
отображается в точку
, а точка
отображается в
.
- Дробно-линейное отображение можно представить в виде суперпозиции трех простейших отображений: целого линейного
, отображения
и сдвига
.
- Дробно-линейное отображение отображает окружности и прямые в окружности и прямые. При этом прямая может перейти как в прямую, так и в окружность. Окружность тоже может перейти как в прямую, так и в окружность. Это свойство называется круговым свойством дробно-линейных отображений.
- Точки симметричные относительно прямой или окружности переходят в точки симметричные относительно образа этой прямой или окружности.
- Дробно-линейное отображение, переводящее три заданные точки в три заданные точки:
дается формулой:
Пример 1 Найти образ мнимой оси при отображении
.
Мнимая ось представляет собой прямую. По третьему свойству она должна перейти в окружность или в прямую. Найдем образы трех точек мнимой оси: 



Пример 2 Найти дробно линейное отображение, переводящее точки
.
Пример 3 Найти образ области
при отображении
Найдем образ мнимой оси при данном отображении. Возьмем три точки : 
Отметим также, что 









Найдем образ точки 
Итак, образ луча 

Теперь мы можем изобразить схему самого отображения:
Пример 4 Найти образы всех квадрантов при отображении .
Чтобы не решать опять задачи подобные примеру 3, воспользуемся следствием принципа симметрии Римана-Шварца в такой формулировке:
Пусть функция 







Пусть 











На следующем рисунке видно, что области 




Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.


Нужна помощь с курсовой или дипломной работой?
📺 Видео
Лекция №12 по ТФКП. Дробно-линейные отображения и их свойства. Городецкий С.Е.Скачать

Теория функций комплексного переменного 17. Конформные отображения. Дробно-линейные отображенияСкачать

Конформные отображенияСкачать

Конформные отображения с помощью дробно-линейной функции: вывод формулы отображения по 3 точкамСкачать

Конформные отображения с помощью линейной функцииСкачать

Конформные отображения с помощью показательной и логарифмической функцийСкачать

Конформные отображения с помощью степенной функцииСкачать

2 4 Линейные отображения примеры и свойстваСкачать

Конформные отображения с помощью функции ЖуковскогоСкачать

ТФКП 14. Дробно-линейные отображения.Скачать

Дробно-линейная функция. 10 класс.Скачать
Лекция №13 по ТФКП. Функция Жуковского. Конформные отображения. Городецкий С.Е.Скачать

Найти пример отображения на верхнюю полуплоскостьСкачать

Теория функций комплексного переменного 18. Конформные отображения элементарными функциямиСкачать

Линейные отображения. ТемаСкачать

Власов В. В. - Комплексный анализ (ТФКП) - Конформные отображенияСкачать

7 1 Матрица линейного отображенияСкачать



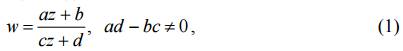
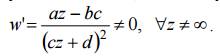
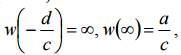
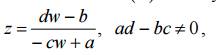
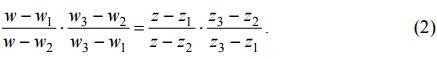
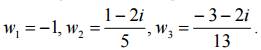
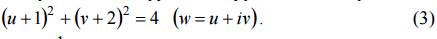
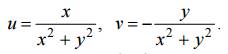
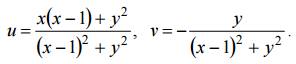
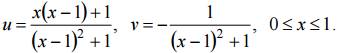
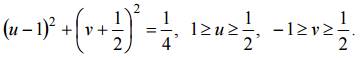
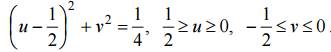








 отображается в точку
отображается в точку  , а точка
, а точка  отображается в
отображается в  , отображения
, отображения  и сдвига
и сдвига  .
. дается формулой:
дается формулой: 
 .
. .
.
 при отображении
при отображении 





