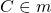Как нарисовать перпендикуляр к треугольнику (2 видео)

Как нарисовать перпендикуляр треугольника

Содержание

Серединный перпендикуляр
Как провести перпендикуляр к прямой — правило построения
Использование транспортира
Циркуль и линейка
Теорема Пифагора
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
Серединный перпендикуляр
Треугольник. Серединный перпендикуляр (медиатриса), средняя линия треугольника.
Характерные особенности медиатрисы треугольника.
Характерные особенности средней линии треугольника.
📽️ Видео

Видео:Построение серединных перпендикуляров треугольника с помощью циркуляСкачать

Серединный перпендикуляр

Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

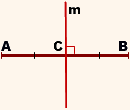
m — серединный перпендикуляр к отрезку AB, если

точка C — середина отрезка AB,

Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:

1) найти середину отрезка;

2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):

Свойства серединного перпендикуляра.

1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).

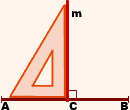
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.

3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Видео:Построение высоты в треугольникеСкачать

Как провести перпендикуляр к прямой — правило построения

Перпендикуляр — это прямая линия, пересекающая другую линию под углом 90°. Построением перпендикуляров на начальном уровне занимаются школьники на уроке геометрии. В будущем эти знания могут пригодиться как в быту, так и в профессиональной сфере. Чтобы правильно провести перпендикуляр к прямой, рекомендуется изучить все возможные способы. Они подразделяются на простые и сложные. Кроме того, для каждого из них потребуются определенные канцелярские принадлежности.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Использование транспортира

Одним из наиболее простых способов построения перпендикуляра к прямой является чертеж при помощи специального инструмента, который называется транспортир. Чтобы правильно начертить отрезок, необходимо по пунктам выполнить следующие действия:

Этот способ широко используется на уроках геометрии. Его преимущество заключается в быстром и простом построении. Для выполнения требуется только транспортир и простой карандаш.

Видео:Построение перпендикуляраСкачать

Циркуль и линейка

Перпендикулярный луч можно опустить на отрезок при помощи еще одного незамысловатого способа. Для этого необходимы простой карандаш, линейка и циркуль. Построить прямой угол можно, выполнив следующие действия:

На отрезке от заданной точки необходимо, используя циркуль, провести две одинаковые дуги. Чтобы расстояние было идентичным с каждой стороны, нужно иглу циркуля поставить в отмеченную точку и при помощи линейки раствор циркуля отодвинуть на какое-то расстояние (это индивидуальный показатель). Таким образом нужно начертить две дуги.

Затем необходимо увеличить раствор циркуля и сделать так, чтобы карандаш находился посередине между точкой справа (слева) и исходной.

Так нужно нарисовать две дуги: одну над прямой, а другую — под ней.

Потом необходимо нарисовать вторую такую дугу. При этом раствор циркуля изменять не требуется. Отметку пересечения двух дуг (правой и левой) нужно обозначить.

Точку пересечения этих двух дуг нужно состыковать с точкой на исходном отрезке. Соединять и проводить линию лучше с использованием линейки. Так рисунок получится ровным и аккуратным.

В результате этих действий должен получиться перпендикуляр, составляющий с прямой линией угол в 90°. Метод более сложный, если сравнивать его с первым. Его целесообразно использовать в том случае, если под рукой не оказалось транспортира.

Видео:Серединные перпендикуляры в треугольникеСкачать

Теорема Пифагора

Чтобы построить перпендикуляр по этому способу, мало знать одного определения, поскольку потребуется теорема Пифагора и ее доказательство. Наиболее распространенный вариант — свойство египетского треугольника со сторонами 5, 4 и 3.

От основной точки А необходимо отмерить и отметить отрезок, равный 3. В результате получается точка В. Далее необходимо построить две одинаковые окружности. При этом центр первой будет располагаться в А, а центр второй — в В. Отметка пересечения этих окружностей обозначается как С. Значит, искомый перпендикуляр — это линия, соединяющая две точки (А и С). Конечно, этот способ лучше посмотреть наглядно на картинке или показать в виде чертежа.

Эту тему проходят на геометрии в 7 классе. Школьники должны дать определение перпендикуляра к прямой. А на его основании построить линию его под углом 90°.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Please wait.

Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

We are checking your browser. mathvox.ru

Видео:Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Эксперт (Короткометражка, Русский дубляж)Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Cloudflare Ray ID: 6d7f5985f8c600b8 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Геометрия 7 класс (Урок№11 - Перпендикуляр к прямой.)Скачать

Серединный перпендикуляр

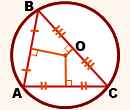
m — серединный перпендикуляр к отрезку AB, если

точка C — середина отрезка AB,

Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:

1) найти середину отрезка;

Свойства серединного перпендикуляра.

Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).

Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Треугольник. Серединный перпендикуляр (медиатриса), средняя линия треугольника.

Формулировка серединный перпендикуляр к отрезку или медиатриса звучит так — прямая, прочерченная через середину стороны под углом 90 0 .

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Характерные особенности медиатрисы треугольника.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Правильна будут и такая формулировка: любая точка, равноудаленная от концов отрезка, размещена на серединном перпендикуляре к нему.

Центр описанной окружности находится в месте пресечения медиатрис треугольника. Следует отметить, что у остроугольного треугольника эта точка размещается внутри, у тупоугольного — за пределами треугольника, у прямоугольного — посредине гипотенузы.

Средняя линия трехугольника – отрезок, соединяющий середины двух его сторон. Общеизвестно, что у треугольника три стороны, и логично, что и три средние линии.