Относительно земли траектория движения колеса велосипеда окружность или прямая линия

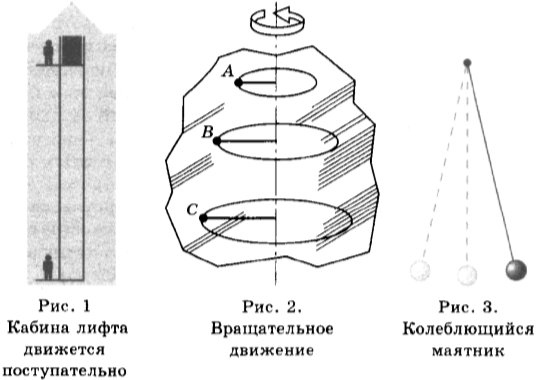
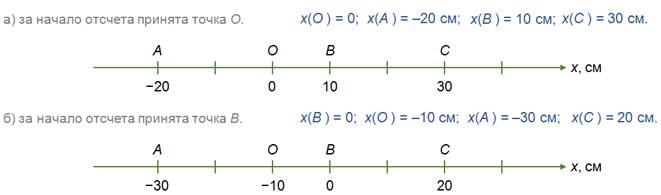1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).

Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).

Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).

2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.

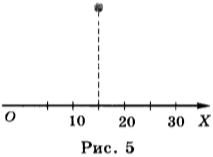
Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).

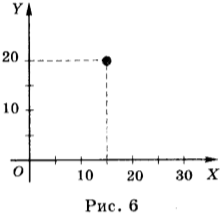
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.

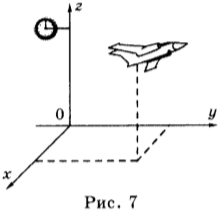
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).

Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.

Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).

3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.

Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.

Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.

Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.

Раздел механики, изучающий способы описания движения тел, называют кинематикой.

4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.

Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.

Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.

Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.

Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.

В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.

Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.

5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.

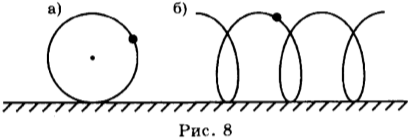
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).

6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.

Если известны траектория тела, его начальное положение и пройденный им путь за время ​ ( t ) ​, то можно найти положение тела в момент времени ​ ( t ) ​. (рис. 9)

Путь обозначают буквой ​ ( l ) ​ (иногда ​ ( s ) ​), основная единица пути 1 м: ( [,mathrm,] ) = 1 м. Кратная единица пути — километр (1 км = 1000 м); дольные единицы — дециметр (1 дм = 0,1 м), сантиметр (1 см = 0,01 м) и миллиметр (1 мм = 0,001 м).

Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.

7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.

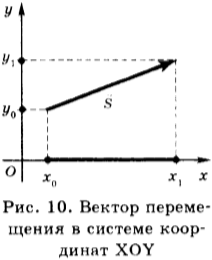
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)

Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается ​ ( overrightarrow ) ​. Единица перемещения ( [,mathrm,] ) = 1 м.

Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.

Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.

Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.

При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.

Координаты начала перемещения — ( x_0, y_0 ) ; координаты конца перемещения — ( x_1, y_1 ) . Проекция вектора перемещения на ось ОХ равна: ​ ( s_x=x_1-x_0 ) ​. Проекция вектора перемещения на ось OY равна: ( s_y=y_1-y_0 ) .

Модуль вектора перемещения равен: ​ ( s=sqrt ) ​.

Видео:Мгновенный центр вращенияСкачать

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. В состав системы отсчёта входят

1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы

2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно

1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора

4. Относительно какого тела покоится автомобиль, движущийся по автостраде?

1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода

5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с

6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с

7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?

1) прямая
2) окружность
3) дуга
4) винтовая линия

8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь ​ ( l ) ​ и модуль перемещения ​ ( s ) ​ мяча за всё время движения?

1) ( l ) = 3,3 м, ​ ( s ) ​ = 3,3 м
2) ( l ) = 3,3 м, ( s ) = 0,7 м
3) ( l ) = 0,7 м, ( s ) = 0,7 м
4) ( l ) = 0,7 м, ( s ) = 3,3 м

9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?

1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй

10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса ​ ( R ) ​. Чему равны при этом путь ​ ( l ) ​ и модуль перемещения ​ ( s ) ​ точки обода?

1) ( l=2R ) , ​ ( s=2R ) ​
2) ( l=pi R ) , ( s=2R )
3) ( l=2R ) , ( s=pi R )
4) ( l=pi R ) , ( s=pi R ) .

11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор

ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта

12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения

ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная

Часть 2

13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.

Видео:Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать

Какие части велосипеда при его прямолинейном движении описывают относительно земли прямолинейные траектории

Задача по физике 7 класс

Какие части велосипеда при его прямолинейном движении описывают относительно земли прямолинейные траектории, а какие – криволинейные?

Ответ: При прямолинейном движении велосипеда его вращающиеся части — колеса и педали описывают относительно земли криволинейные траектории, а части, неподвижные относительно самого велосипеда — руль, седло, рама, описывают относительно земли прямолинейные траектории.

Видео:7 класс урок №8 Относительность механического движенияСкачать

Относительно земли траектория движения колеса велосипеда окружность или прямая

Видео:Велопутешествие на Алтай из Москвы в одиночку. Новосибирская область. КаргатСкачать

Относительно земли траектория движения колеса велосипеда окружность или прямая

Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?

В системе отсчета, связанной с винтом, точка на конце лопасти не двигается. Следовательно, ее траектория в данной системе отсчета представляет собой точку.

А траектория чьего движения и относительно чего может представлять из себя прямую, окружность или винтовую линию?

Я лично отметила верным 3) вариант. Ведь точка на конце лопасти движется вокруг винта по окружности.

Винт вертолета и состоит из лопастей. Поэтому точка на лопасти в системе отсчета винта не двигается, ее траектория — точка. Правильный ответ — 1.

А вообще, любое движение относительно. Траектория материальной точки в разных системах отсчета будет выглядеть по-разному. В качестве примера, будем следить все за той же точкой на конце лопасти вертолета. В системе отсчета, жестко связанной с любой точкой самого вертолета, например с креслом пилота, траектория конца лопасти будет представлять собой окружность. Если следить за нашей точкой с Земли, то, поскольку вертолет понимается, а лопасть вращается, точка будет двигаться по винтовой линии. Наконец, если на земле ровно под осью вращения винта разместить карусель и вращать ее со скоростью винта, то в системе координат, связанной с такой каруселью наша точка будет подниматься вертикально вверх.

На мой взгляд не совсем корректная формулировка.

В системе отсчёта, связанной с НЕПОДВИЖНЫМ винтом, траектория — окружность.

В системе отсчёта, движущейся (вращающейся) вместе с винтом, траектория — точка.

3357 я не могу понять в чем cуть этих задач. как их правильно решать! я не понимаю!

Это скорее вопрос, а не задача. Нужно просто представить себе, как движется одна точка в некоторой определенной системе отсчета, ничего более.

а если бы ну жно было определить троекторию точки относительно земли, то ответ был бы винтовая линия? ну спираль типа?

точка находится на краю лопасти винта вертолёта.

Если бы в вопросе было относительно лопасти то была бы точка, а в этом случае относительно винта (винт- это место соединения лопастей) http://s019.radikal.ru/i642/1301/9e/ae1cfece98dc.jpg

Спасибо за картинку. Насколько я понимаю, лопасти и образуют винт вертолета. В любом случае, лопасти жестко связаны с винтом. Винт вертолета сам относительно себя не двигается, поэтому траектория будет точкой.

Встретил такое задание в книге издательства «Экзамен» по подготовке к ЕГЭ, автор Олег Фёдорович Кабардин, в данной книге ответ окружность

Здравствуйте, я решаю у вас задания для подготовки к ЕГЭ ,и одновременно решаю задания в других задачниках , и мне очень не понравился ваш ответ в данной задаче, и через день я нашел такую же задачу в другом задачнике ( если надо, могу сфотографировать и задачу, и ответ, и книгу) там был такой же ответ, какой я и думал, траектория движ точки — окружность! прошу отреагировать

Выше данный вопрос уже обсуждался. Винт сам относительно себя не двигается, поэтому интересующая нас точка покоится. Траектория — точка. Вот в системе отсчета, связанной с вертолетом, будет окружность. А относительно земли — винтовая линия

Видео:Физика - движение по окружностиСкачать

Основные понятия кинематики. Относительность движения (практика)

Урок 2. Подготовка к ЕГЭ по физике. Часть 1. Механика.

Видео:🛡 Защити Свой Двигатель: Подделка vs Качество. Тест Масляных Фильтров ВАГ! 🚗💪Скачать

В данный момент вы не можете посмотреть или раздать видеоурок ученикам в личном кабинете

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно его приобрести.

Получите невероятные возможности

Конспект урока «Основные понятия кинематики. Относительность движения (практика)»

В данной теме будет рассмотрено решение некоторых типовых задач по кинематике.

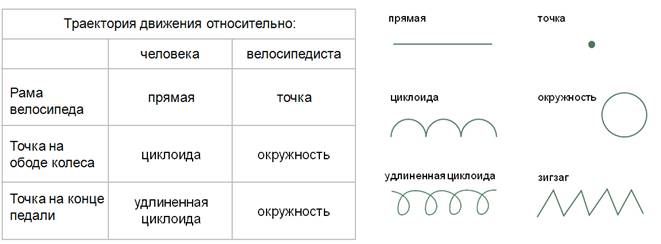
Задача 1. Велосипедист движется по прямолинейному гладкому участку дороги. Каковы траектории движения относительно велосипедиста и относительно стоящего на обочине человека рамы велосипеда; точки на ободе колеса; точки на конце педали?

Начнем с определения вида траектории рамы велосипеда. Здесь все очень просто: так как относительно велосипедиста рама неподвижна, то траекторией ее движения будет являться точка.

Относительно же человека, стоящего на обочине дороги, рама будет двигаться прямолинейно, «вычерчивая» в воздухе прямую линию.

Теперь исследуем движение точки, располагающейся на ободе колеса, относительно велосипедиста. Представьте, что вы сели на велосипед, приметили положение ниппеля на переднем колесе и не спеша надавили на педаль, не выпуская ниппель из поля зрения. Какую траекторию описывает ниппель.

Точка, располагающаяся на ободе колеса, относительно велосипедиста, описывает окружность. Аналогично будет себя вести и точка, находящаяся на конце педали

Теперь разберемся с траекторией движения точки на ободе колеса, относительно человека, стоящего на обочине. Вновь обратимся к мысленному эксперименту. Мы стоим на обочине, а мимо нас проезжает велосипедист. Зафиксировали взгляд на какой-либо точке колеса (пусть это будет, например, светоотражатель на конце спицы) и проследим за ее траекторией.

Получаются кривые, которые принадлежат семейству циклоид. Значит траекторией движения точки на ободе колеса относительно неподвижного человека на обочине является циклоида.

Траекторией движения точки на конце педали относительно неподвижного человека на обочине будет являться удлиненная циклоида.

Задача 2. Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) пути, пройденного Землей по орбите вокруг Солнца за месяц; в) длины экватора и г) скорости движения Земли по орбите вокруг Солнца?

Тело можно принять за материальную точку, если:

1) тело движется поступательно;

2) размеры тела много меньше расстояния, которое оно проходит;

3) размеры тела много меньше расстояния до тела отсчета.

Рассмотрим вариант а более подробно. Для это проверим выполнение выше названных условий. Согласно первому условию, тело должно двигаться поступательно. Для этого случая оно не выполняется, так как о движении Земли в условии задачи ничего не говорится. Второе условие материальной точки также не выполняется, так как не известно расстояние, пройденное Землей. По третьему условию размеры тела должны быть намного меньше расстояния до тела отсчета. В данном случае, тело отсчета — это Солнце. Среднее расстояние от Земли до Солнца составляет 149,6 миллионов км, а средний радиус нашей планеты всего 6371 км, что, конечно же, намного меньше среднего расстояния до Солнца.

Следовательно, в первом примере Землю можно принять за материальную точку, так как выполняется третье условие.

Во втором примере Землю можно принять за МТ, т. к. ее размеры много меньше расстояния, которое она проходит по орбите за месяц.

В примере «в» Землю нельзя считать МТ, т. к. при расчете длины экватора Земли нельзя пренебречь ее размерами.

В последнем примере Землю можно считать МТ, т. к. размеры Земли (радиус 6371 км) во много раз меньше расстояния до Солнца (149,6 млн. км).

Задача 3. На рисунке указаны положения точек А, О, В, С и направление оси Х. Перерисуйте рисунок и определите координаты точек, если: а) за начало отсчета принята точка О; б) за начало отсчета принята точка В.

Задача 4. Мяч вертикально упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Сделайте чертеж. Найдите путь и модуль перемещения мяча.

«Упражнение, друзья, даёт больше,

Видео:ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Относительно Земли траектория движения колеса велосипеда:
Прямая линия или окружность

Видео:Механическое движение | Физика 7 класс #9 | ИнфоурокСкачать

Ответы

по специальной договоренности с редколлегией и редакцией журнала «квант»

движению тела обычно препятствуют силы трения. если соприкасаются поверхности твердых тел, их относительному движению мешают силы сухого трения. характерной особенностью сухого трения является существование зоны застоя. тело нельзя сдвинуть с места, пока абсолютная величина внешней силы не превысит определенного значения. до этого момента между поверхностями соприкасающихся тел действует сила трения покоя, которая уравновешивает внешнюю силу и растет вместе с ней (рис. 1).

максимальное значение силы трения покоя определяется формулой

где μ— коэффициент трения, зависящий от свойств соприкасающихся поверхностен; n — сила нормального давления.

когда абсолютная величина внешней силы превышает значение fтр max, возникает относительное движение — проскальзывание. сила трения скольжения обычно слабо зависит от скорости относительного движения, и при малых скоростях ее можно считать равной fтр max.

движению тела в жидкости и газе препятствуют силы жидкого трения. главное отличие жидкого трения от сухого — отсутствие зоны застоя. в жидкости или газе не возникают силы трения покоя, и поэтому даже малая внешняя сила способна вызвать движение тела. сила жидкого трения при малых скоростях пропорциональна скорости, а при больших — квадрату скорости движения.

1. при экстренной остановке поезда, двигающегося со скоростью υ = 70 км/ч. тормозной путь составил s = 100 м. чему равен коэффициент трения между колесами поезда и рельсами? каким станет тормозной путь, если откажут тормоза в одном из n = 10 вагонов? массу локомотива принять равной массе вагона; силами сопротивления воздуха пренебречь.

при торможении ускорение а поезду сообщает сила трения fтр:

где μ — масса всего состава. сила трения представляет собой равнодействующую всех сил трения, действующих на состав (рис. 2), и равна по модулю .

с другой стороны, . подставляя это значение в выражение для μ, получаем

в том случае, когда не работают тормоза у одного из вагонов, суммарная сила трения, действующая на вагоны и локомотив, равна

где m — масса одного вагона. масса всего состава равна μ = (п + 1)∙m, так что . ускорение поезда в этом случае равно

🔍 Видео

Как исправить и протянуть колесо велосипедаСкачать

Как надеть любую покрышку? Лайфхак😱Скачать

Виды механического движения.Скачать

Неисправное мотор колесоСкачать

Лекция по аааа механике ааа, Движение. #2Скачать

Как снять колёса велосипедаСкачать

Как выровнять восьмёрку на колесе велосипедаСкачать

Wheel Repair Как правильно исправлять восьмёрки на колесе ВелосипедаСкачать

Бескамерные колеса 😎Скачать

Правка восьмерки на колесе велосипедаСкачать

Какое давление качать в колеса велосипеда?Скачать

покрышки не садятся, что нужно проверитьСкачать