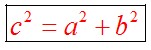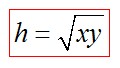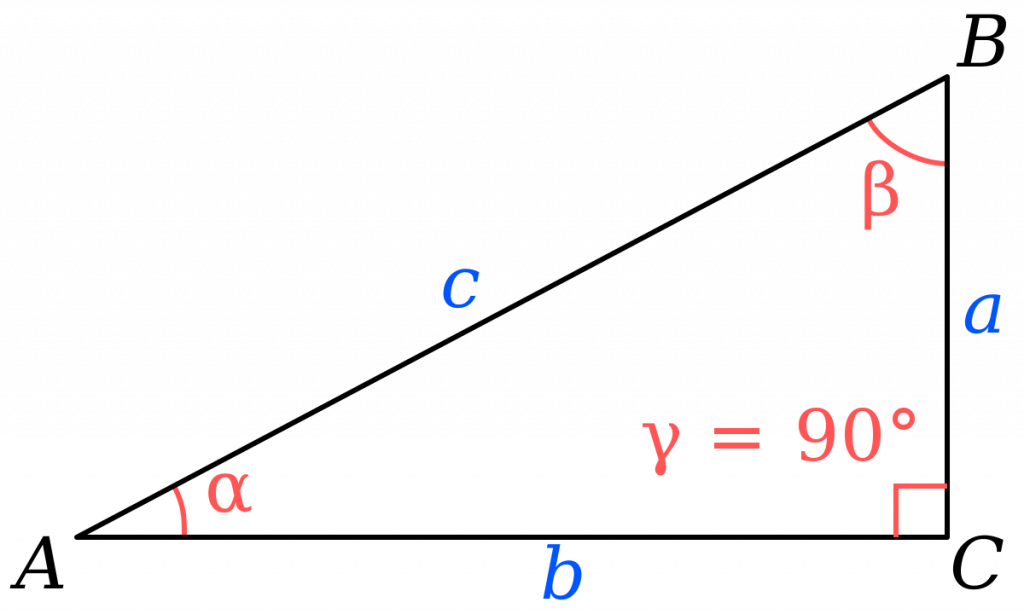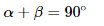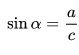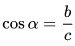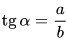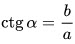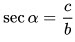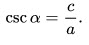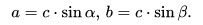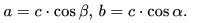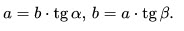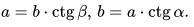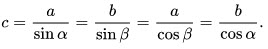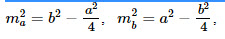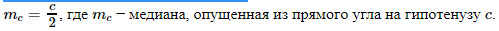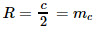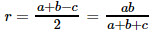Отношение сторон прямоугольного треугольника (2 видео)

Отношение сторон прямоугольного треугольника

Свойство. Сумма двух острых углов прямоугольного треугольника равна 90 0

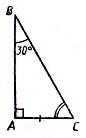
Свойство. Катет прямоугольного треугольника, лежащий против угла в 30 0 , равен половине гипотенузы.

Теорема. Два прямоугольных треугольника равны, если катеты одного равны катетам другого.

Теорема. Два прямоугольных треугольника равны, если гипотенуза и катет одного равны гипотенузе и катету другого.

Теорема. Два прямоугольных треугольника равны, если острый угол и сторона одного равны острому углу и стороне другого.

Содержание

Теорема Пифагора
Соотношение углов и сторон прямоугольного треугольника
Прямоугольные треугольники
Некоторые свойства прямоугольного треугольника:
Соотношение между сторонами и углами в прямоугольном треугольнике:
Значения тригонометрических функций некоторых углов:
Все формулы прямоугольного треугольника — примеры расчетов
Формулы
🎬 Видео

Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Теорема Пифагора

Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема, обратная теореме Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Соотношение углов и сторон прямоугольного треугольника

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Важные значения! ИХ ОБЯЗАТЕЛЬНО ЗАПОМНИТЬ!

Высота прямоугольного треугольника, проведенного из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

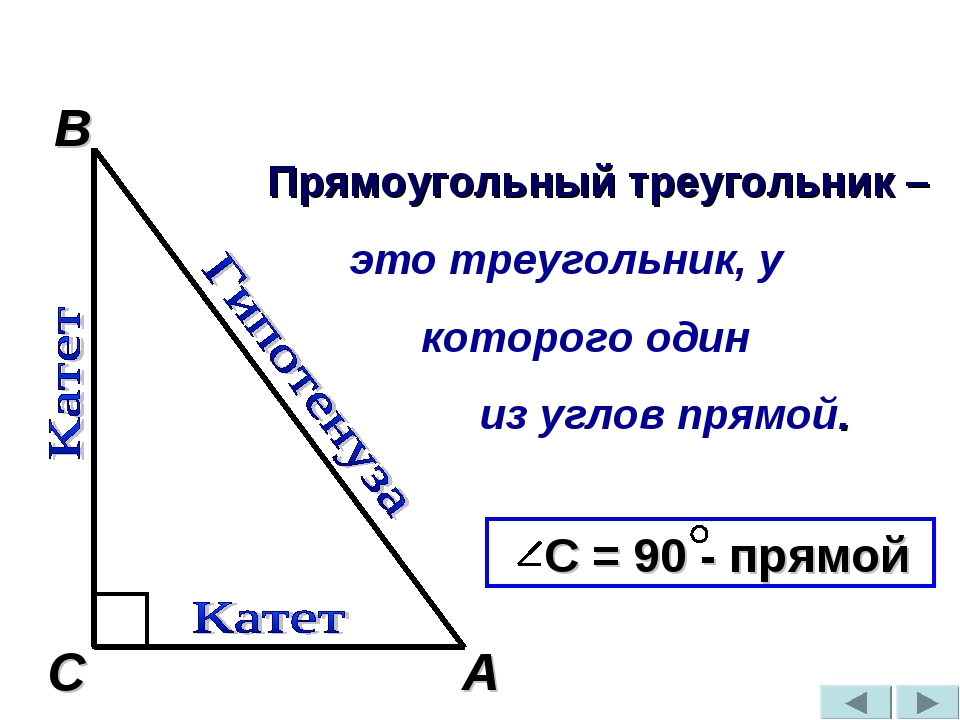
Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

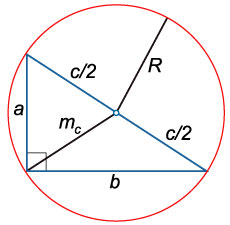
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

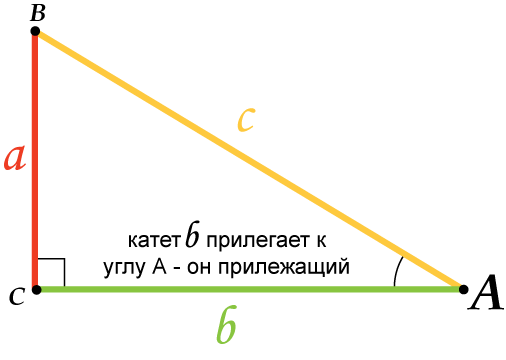
Соотношение между сторонами и углами в прямоугольном треугольнике:

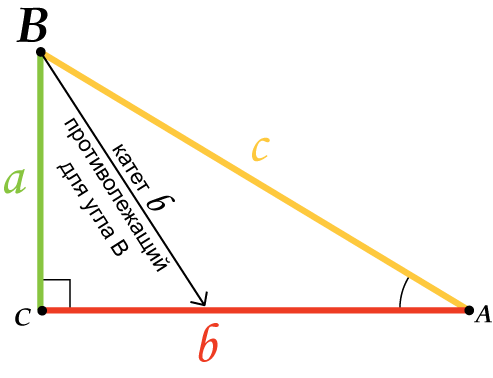
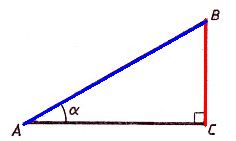
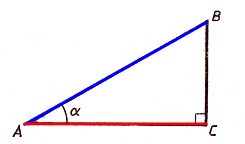
В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=/, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

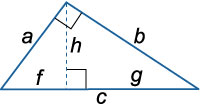
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Все формулы прямоугольного треугольника — примеры расчетов

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Формулы

1. Сумма острых углов прямоугольного треугольника равна 90 0 :

2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:

3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:

4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:

5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:

6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:

7. Косеканс острого угла равен отношению гипотенузы к противолежащему:

8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:

9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:

10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:

11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:

12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):