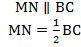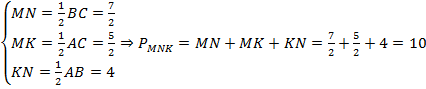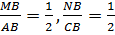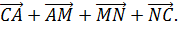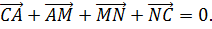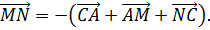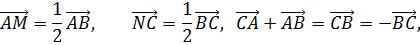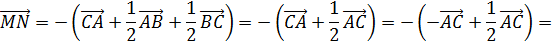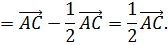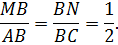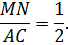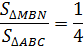Треугольник образованный средними линиями

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

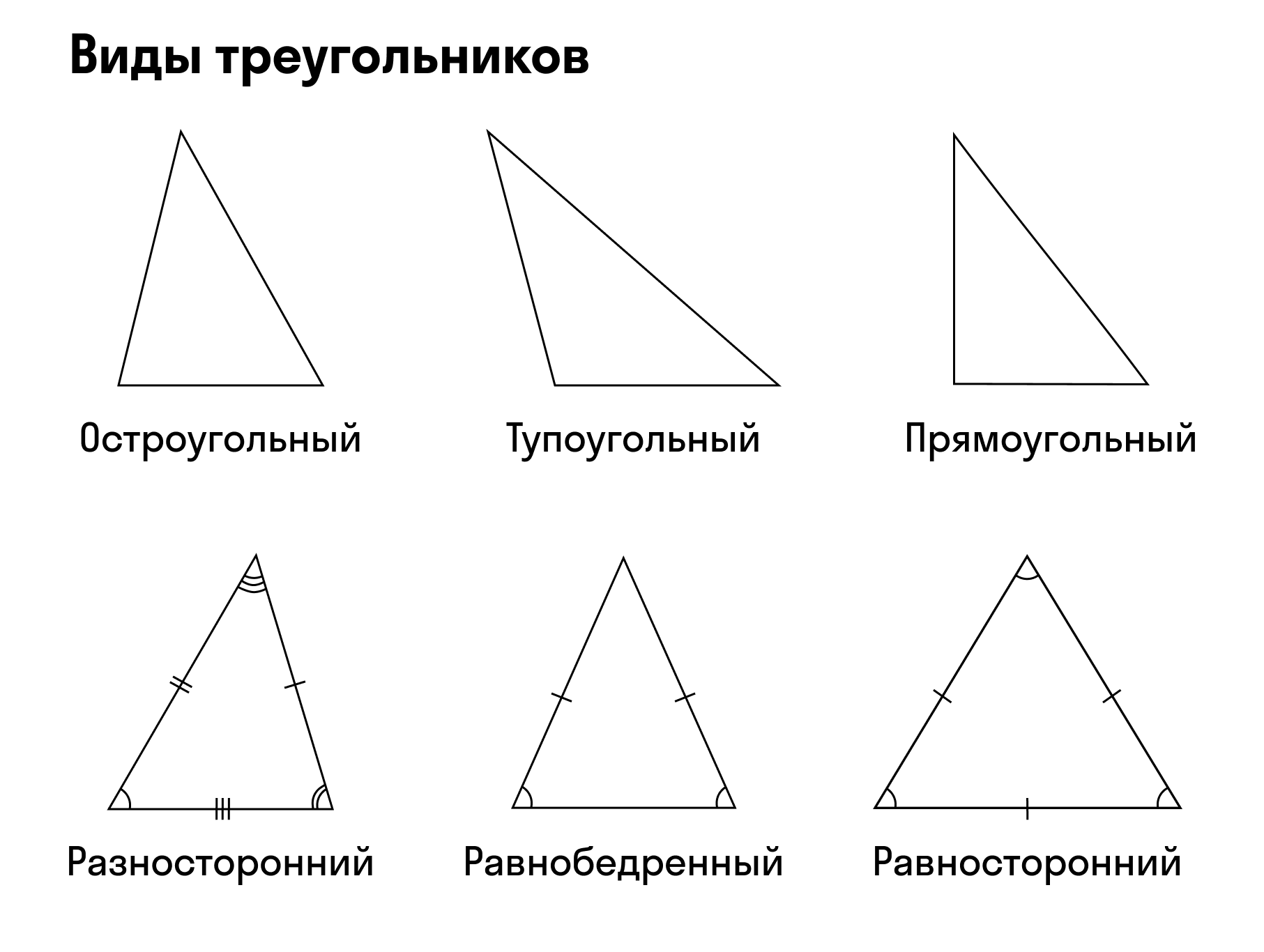
• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

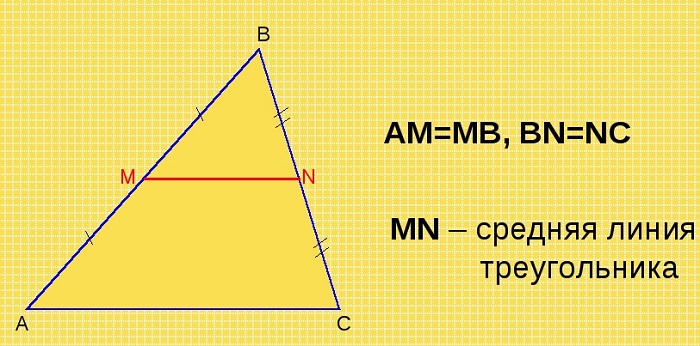
​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:Геометрия Докажите, что периметр треугольника, стороны которого являются средними линиямиСкачать

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

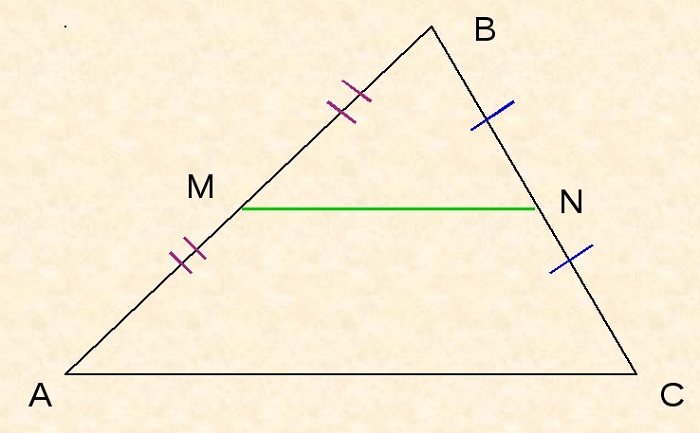
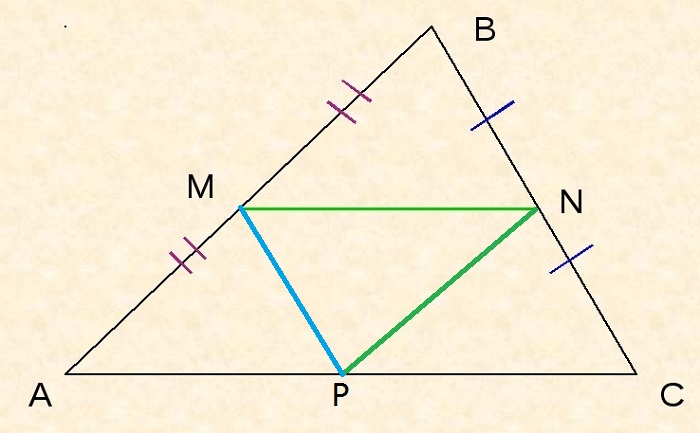
Докажем теорему:

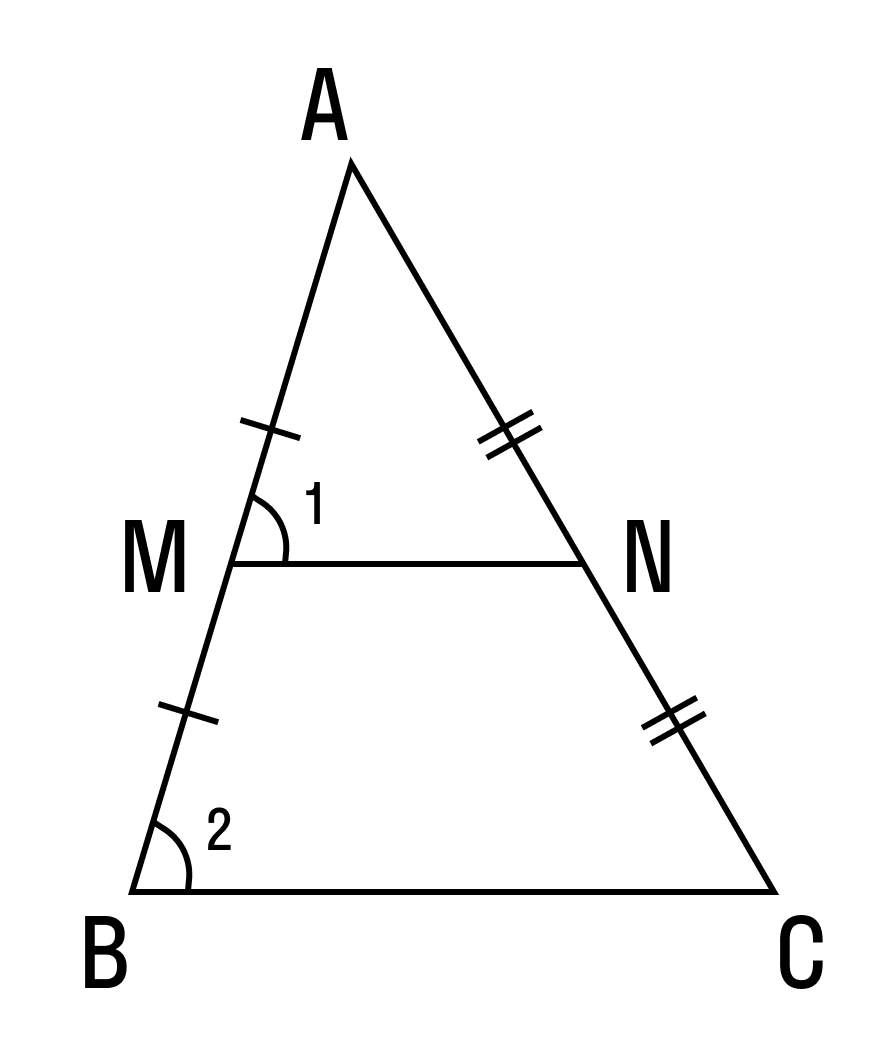
По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.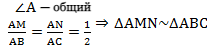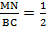

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

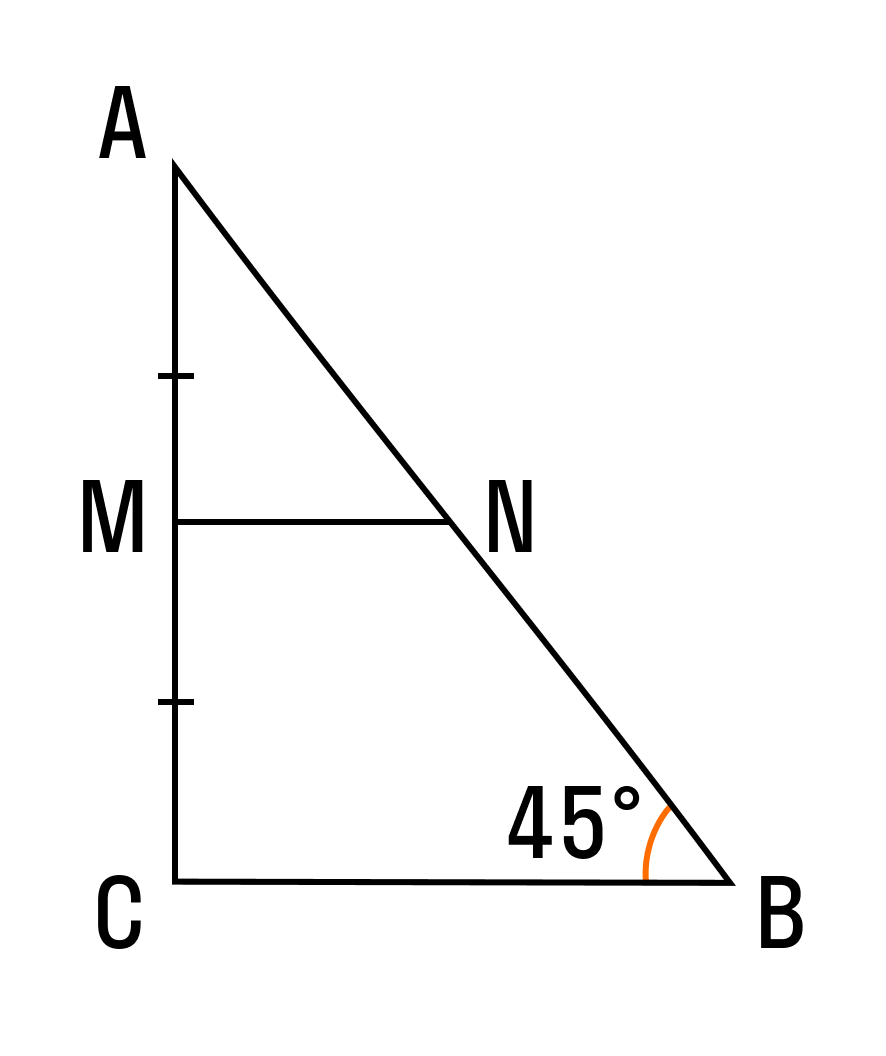
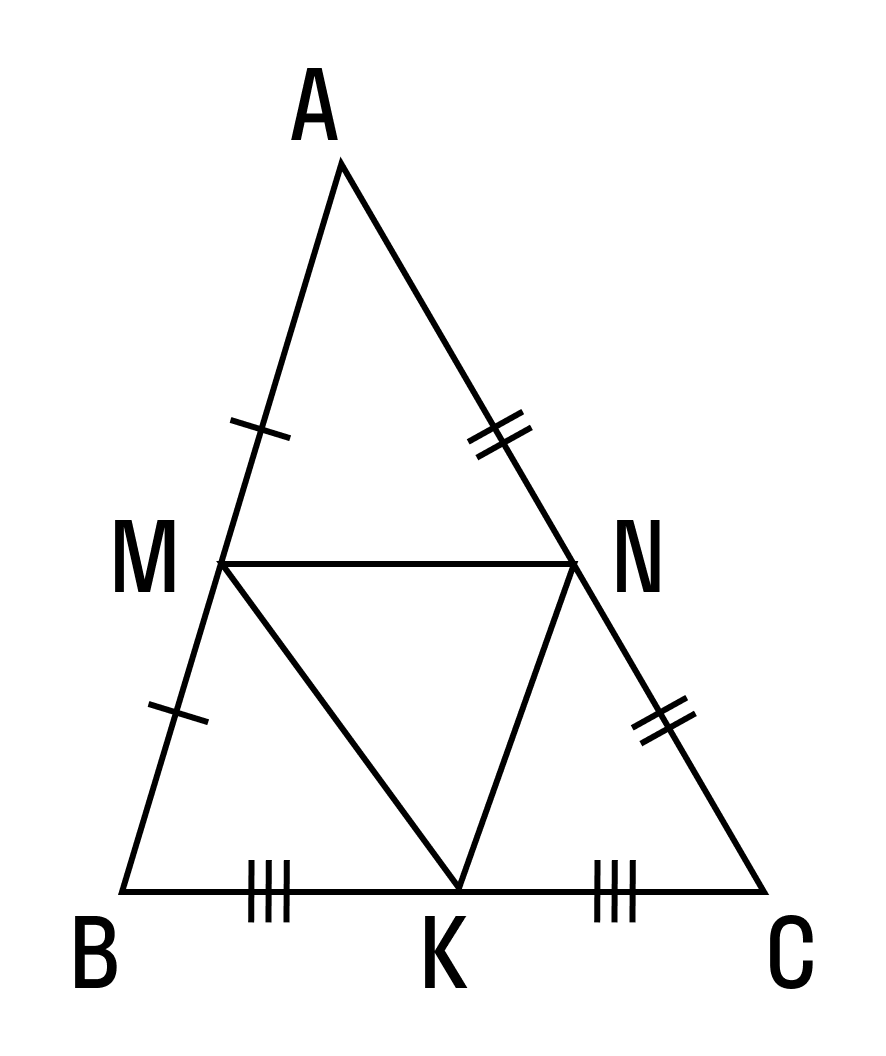
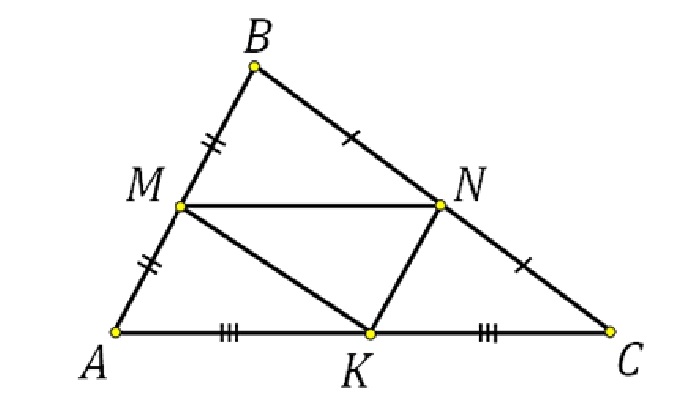
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

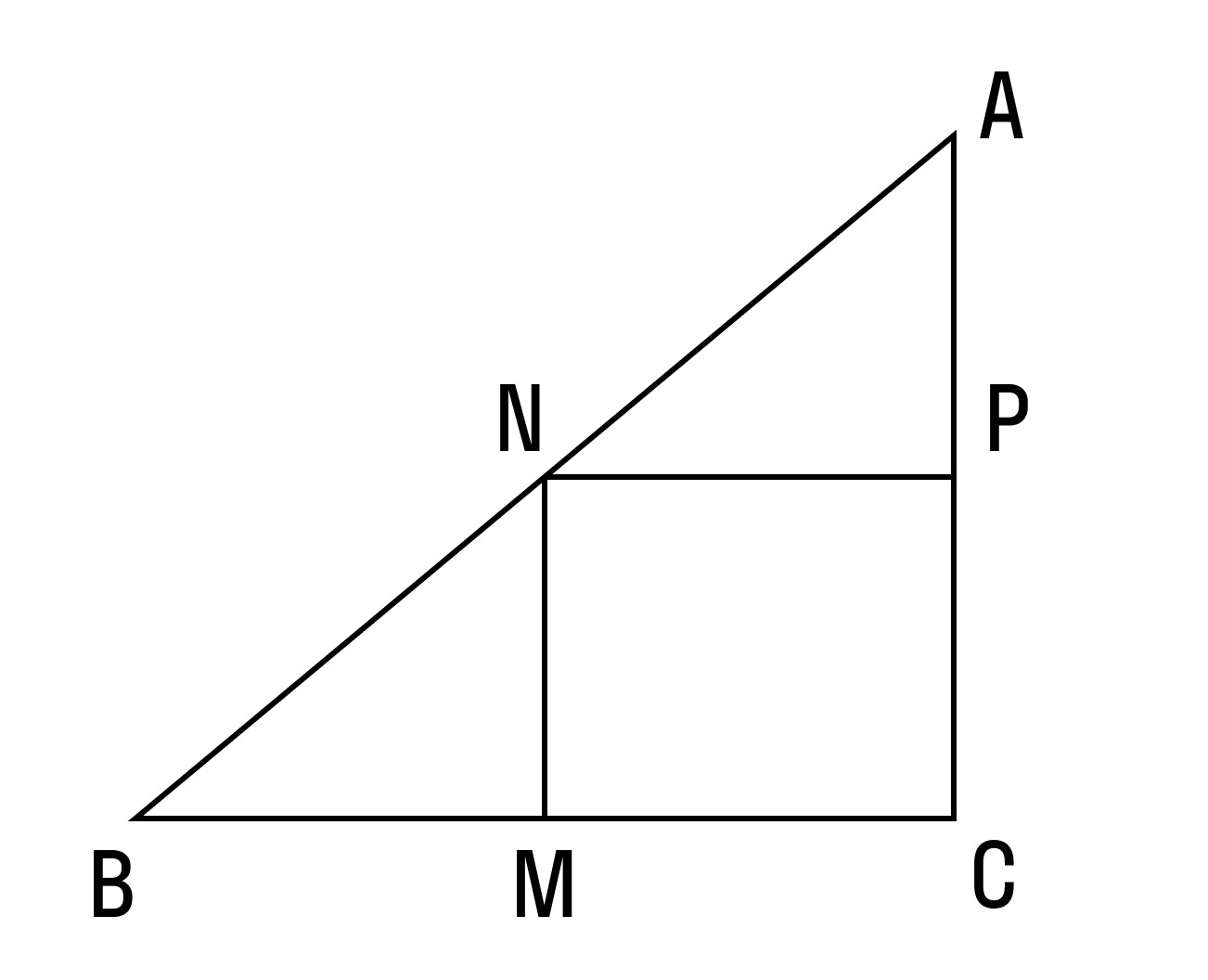
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Определение и признаки средней линии треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

Видео:Геометрия 8. Урок 7 - Средняя линия треугольника и трапецииСкачать

Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Видео:Средняя линия треугольника. Видеоурок 13. Геометрия 8 класс.Скачать

Следствия из теоремы с доказательствами

Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

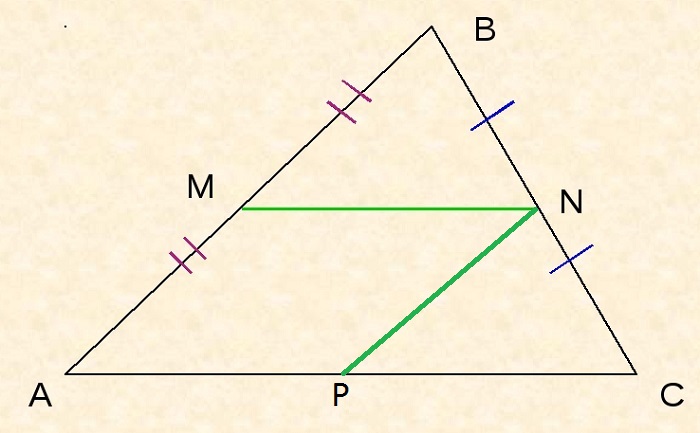
Следствие №2

Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Видео:№564. Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника,Скачать

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Видео:Треугольник из средних линий данного треугольникаСкачать

Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Видео:МАТЕМАТИКА | Средняя линия треугольникаСкачать

Пример решения задачи

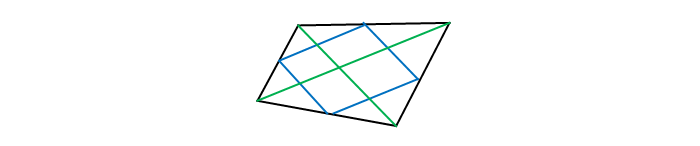
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Треугольник, образованный средними линиями равнобедренного треугольника, называется : а) прямоугольным б) равносторонним помогите пож?

Геометрия | 5 — 9 классы

Треугольник, образованный средними линиями равнобедренного треугольника, называется : а) прямоугольным б) равносторонним помогите пож.

Он не может называться ни равносторонним ни прямоугольным, так как две средние линии равны половине боковых (равных) сторон, а третья равна половине основания — этот треугольник будет равнобедренным.

Если угол при вершине равен 90 градусов, то он будет еще и прямоугольным, но об углах ничего не сказано.

Ответ, оба варианта неверны.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Люди, пожалуйста помогите?

Люди, пожалуйста помогите!

Прямоугольная трапеция диагональю разделена на 2 треугольника.

Один из них равносторонний треугольник со стороной а, а второй — прямоугольный треугольник.

Найдите среднюю линию трапеции.

Видео:Геометрия. 7 класс. Медианы, биссектрисы, высоты и средние линии треугольника /13.10.2020/Скачать

Площадь равностороннего треугольника ABC равна 60см в квадрате?

Площадь равностороннего треугольника ABC равна 60см в квадрате.

Найдите площадь треугольника, образованного средними линиями треугольника ABC.

Видео:СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА 8 класс Атанасян геометрияСкачать

Прямоугольная трапеция разделяется диагональю на два треугольника — равносторонний со стороной а и прямоугольный?

Прямоугольная трапеция разделяется диагональю на два треугольника — равносторонний со стороной а и прямоугольный.

Найдите среднюю линию трапеции.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

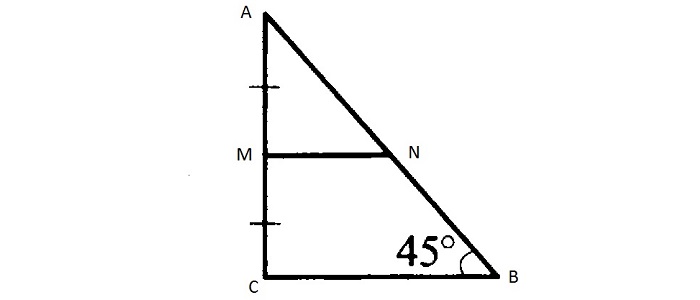
Средняя линия отсекает от данного треугольника равнобедренный прямоугольный треугольник?

Средняя линия отсекает от данного треугольника равнобедренный прямоугольный треугольник.

Найдите углы данного треугольника.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Треугольник образованный средними линиями прямоугольного треугольника является каким?

Треугольник образованный средними линиями прямоугольного треугольника является каким?

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Площадь равностороннего треугольника АВС равна 60 см?

Площадь равностороннего треугольника АВС равна 60 см.

Найдите площадь треугольника , образованного средними линиями треугольника АВС.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Помогите решить?

Прямоугольная трапеция делится диагональю на два треугольника — — равносторонний со стороной а и прямоугольный.

Найдите среднюю линию трапеции.

Периметр равностороннего треугольника равен 45 см?

Периметр равностороннего треугольника равен 45 см.

Найдите периметр треугольника, который образован средними линиями заданного треугольника.

Прямоугольная трапеция делится диагональю на прямоугольный и равнобедренный треугольники?

Прямоугольная трапеция делится диагональю на прямоугольный и равнобедренный треугольники.

Найдите среднюю линию трапеции, если периметр равностороннего треугольника равен 27дм помогите пожалуйста с решением ответ должен получиться6.

75дм можно с чертежом.

Треугольник образован средними линиями равнобедренного треугольника является ?

Треугольник образован средними линиями равнобедренного треугольника является :

Вопрос Треугольник, образованный средними линиями равнобедренного треугольника, называется : а) прямоугольным б) равносторонним помогите пож?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Угол 2 = 180 — 130 = 50 Углы два и три вертикальных следовательно угол 2 равен углу 3 Угол 4 90 — 50 = 40 Ответ : 1угол — 50градусов 2угол — 50градусов 3угол — 40градусов.

1. Найдем координатыАС = (2 + 3 ; — 1 + 1) = (5 ; 0) ВD = ( — 2 + ( — 1) ; — 4 + 1) = ( — 3 ; — 3) ; AC = [tex] sqrt < (2 — 3) ^ + ( — 1 — 1 ) ^ > = sqrt ; BD = [tex] sqrt < ( — 2 + 1 ) ^ + x( — 4 — 4) ^ > = sqrt ; 2) коо..

P = 2(AB + BC) AB = x + 8 BC = x P = 104 104 = x + x + 8 X = 22 BC = 22 AB = 22 + 8 = 30.

По теореме пифагора √169 — 25 = √144 = 12.

Можно решить и по теореме Пифагора.

Точки А, В, С не могут лежать на одной прямой.

Треугольники подобныпо двум сторонам и углу между ними следовательно A1C1 в 4 раза меньше. A1C1 = 30 / 4 = 7. 5 м.

ПЛОЩАДЬ ТРАПЕЦИИ = полусумма длин оснований * на высотув трапеции проводим высоту СН, рассмотрим треугольник СДНуголД = 45 градусовугол Н = 90 градусовиз этого следует, что уголС = 45 градусов, а из этого следует треугольник СДН — равнобедренныйСН = ..

Внешний угол треугольника равен сумме двух других углов (не смежных с ним) , АВ = ВС, значит угол А равен углу С, получаем С = 70 / 40 = 1. 75.

Гипотенуза АВ по т. Пифагора равна BC = корень(AB ^ 2 + AC ^ 2) = корень(10 ^ 2 + 6 ^ 2) = корень(136) = 2 * корень(34)По определению синуса острого угла прямоугольного треугольникаsin B = AC ABsin B = 10 (2 * корень(34)) = 5 (корень(34))ответ..