Надо только постараться и запомнить
Всё, как есть: 3, 14, 15, 92 и 6.
Введение
Данная тема представляет определенный интерес, поскольку её истоки относятся к древности:с давних пор люди пытались решать задачи, связанные с кругом – измерять длину окружности, находить площадь круга.
Любой школьник сегодня должен уметь находить длину окружности и площадь круга, первый опыт вычислений происходит в 6 классе. Но, к сожалению, эти знания остаются для многих формальными, и уже через годмало кто помнит не только то, что отношение длины окружности к её диаметру одно и то число, но даже с трудом вспоминают численное значение числа π, равное 3,14.
В ходе работы над проектом появляется возможность не только усвоить формулы для нахождения длины окружности и площади круга, нои приподнять завесу богатейшей истории числа π, которым человечество пользуется уже много веков.
Актуальность проекта заключается в том, что появляется возможность не только усвоить формулы для нахождения длины окружности и площади круга, но и создать информационный продукт в виде буклета, который будет содержать не только основные понятия и формулы по теме «Длина окружности и площадь круга», но и интересные факты и исторические сведения.
Гипотеза: Длина окружности, её радиус и площадь связаны между собой посредством формул.
Цель работы: Исследование числа π и выявление его роли в окружающей среде . Задачи работы: 1. Познакомиться подробнее с числом π. 2. Провести практическую работу нахождения числа π. 3. Найти занимательные факты и правила для запоминания числа π.
4.Изучить формулу площади круга.
5.Научится создавать буклеты с помощью текстового процессора MicrosoftWord.Предмет исследования: окружность.
Объект исследования: отношение длины окружности к диаметру.
Методы исследования: эксперимент, наблюдение, анализ.
Ожидаемые результаты: Некоторые данные и формулы достаточно трудно запоминаются, но с помощью открытия интересных фактов о числах или понятиях, можно лучше запомнить формулы, правила. Создание буклета с помощью MicrosoftOffice.
Глава 1. Теоретическая часть
У круга есть одна подруга.
Известна всем её наружность.
Она идёт по краю круга
1.1. Понятие окружности
Окружность – это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности.
Точка О – центр окружности. R –радиус окружности (это отрезок, соединяющий центр окружности с любой ее точкой). По-латыни radius – это спица колеса.
1.2. Длина окружности.
Если разрезать окружность в какой-либо точке и распрямить её, то получим отрезок, длина которого и есть длина окружности.
Отношение длины окружности к её диаметру есть одно и то же число для всех окружностей. Установлено, что какой бы ни была окружность, отношение ее длины к диаметру является постоянным числом. Это число принято обозначать буквой π.
Более точное его значение 3,1415926535897932… [1, стр.189]
Обозначим длину окружности буквой С, а ее диаметр буквой d , то, тогда формулы для вычисления длины окружности С = πd.
Если известен радиус окружности, то формула длины окружности будет выглядеть следующим образомC = 2πr.
1.3. Круг. Площадь круга
Круг – это часть плоскости, ограниченная окружностью.
Площадь круга вычисляется по формуле: S=R 2 [2, «Окружность. Круг»]
1.4. Исторические сведения
Ещё в древности пытались решать задачи связанные с кругом. Измерение длины окружности имеет чисто «практическое» решение: можно уложить вдоль окружности нить, а потом развернут её и приложить к линейке ил же отметить на окружности точку и «прокатить» её вдоль линейки (можно, наоборот, «обкатить» линейкой окружность). Так или иначе измерения показывали, что отношение длины окружности к её диаметру одно и то же для всех окружностей. Древние египтяне считали, что длиннее диаметра в 3,16 раза, а римляне – в 3,12 раза. Однако древнегреческих математиков такой опытный подход к определению длины окружности не удовлетворял. К тому же такой подход не позволял определить площадь круга. Выход был найден, впервые известным учёным Архимед предложил первый математический метод вычисления числа π, с помощью расчета вписанных в круг многоугольников.
Это позволяло вычислять значение π не практически – ниткой и линейкой, а математически, что обеспечивало гораздо большую точность. [3, стр. 65-72]
Известный ученый Архимед нашел значение π =, что дает величину 3.1428. В Древней Греции вскоре после Архимеда было получено более точное приближение к числу π = .
В V веке н.э. китайским математиком Цзу Чунчжи было найдено более точное значение π =3,1416927… .
Спустя полтора столетия в Европе нашли число π только с 9 правильными десятичными знаками, сделав 16 удвоений числа сторон многоугольников, но при этом Ф.Виету принадлежит первенство в открывшейся возможности отыскания π. Это открытие имело огромное значение, так как позволило вычислять число π с какой угодно точностью. [4]
Вначале XVII в. Голландский математик из Кельна (Кейлен) Лудольф ван Цейлен затратил 10 лет на вычисление числа Пи и нашел 32 правильных знака после запятой. Изложив свои результаты в сочинении «Об окружности», Лудольф закончил его словами: « У кого есть охота, пусть идёт дальше». С тех пор (1615г.) значение числа π с 32 десятичными знаками получило название числа Лудольфа. [5]
В настоящее время число Пи вычислено с точностью до 10 триллионов знаков после запятой.
Первый миллион знаков после запятой в числе Пи состоит из: 99959 нулей, 99758 единиц, 100026 двоек, 100229 троек, 100230 четвёрок, 100359 пятёрок, 99548 шестёрок, 99800 семёрок, 99985 восьмёрок и 100106 девяток.
Если рассчитать длину экватора с точностью до 1 см – предполагая, что мы знаем длину его диаметра вполне точно – нам достаточно было бы взять π всего с 9 цифрами после запятой. А взяв вдвое больше цифр (18) , мы могли бы вычислить длину окружности, имеющей радиусом расстояние от Земли до Солнца, с погрешностью не свыше 0,0003 мм (волос в 100 раз толще этой возможной ошибки!)
В штате Иллинойс (США) официально принят закон о том, чтобы чисто Пи считать равным 4! [6]
Многие математики утверждают, что правильным будет такая формулировка: «круг – фигура с бесконечным количеством углов». Здорово, правда?!
Есть такая поговорка английского математика Моргана: «Число π лезет в дверь, в окно и через крышу».
14 марта объявлено Всемирным днем числа π. [7]
Вывод: Число π захватывает умы гениев всего мира.
(приложение 1. Портрет числа π)
Глава 2. Исследовательская часть 2.1. Эксперимент 1. Нахождение длины окружности с помощью нити
Практическая работа состояла в том, чтобы найти отношение длины окружности к её диаметру.
Берём шесть круглых предметов, в частности вазу, несколько стаканов и чашек разных размеров.
С помощью нити измеряем длину окружности.
Поставив предмет на лист бумаги, обводим его карандашом, вырезаем бумажный круг, сгибаем пополам и линейкой измеряем длины диаметров.(приложение 2)
Составим таблицу с измеренными данными, последний столбец таблицы вычислительного характера: вычислим с помощью калькулятора отношение длины окружности (столбец 2) к диаметру (столбец 3) .
Видео:Длина окружности. Площадь круга, 6 классСкачать

Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика. 6 класс
Конспект урока
Длина окружности. Площадь круга
Перечень рассматриваемых вопросов:
- окружность, круг и их элементы: радиус, диаметр, хорда;
- понятие длины окружности, площади круга;
- задачи на вычисление длины окружности и площади круга.
Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которую называют центром окружности.
Круг – это часть плоскости, ограниченная окружностью.
Радиус – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
Хорда – это отрезок, соединяющий две точки окружности.
Диаметр – это хорда, проходящая через центр окружности.
Длина окружности вычисляется по формулам: С = πd или С = 2πR, где π ≈ 3, 14 – иррациональное число.
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которая называется центром окружности.
Элементы окружности: центр, радиус, диаметр.
Отрезок, соединяющий две точки окружности, называется хордой.
Диаметр – это хорда, проходящая через центр окружности.
Ещё в древности было установлено, что какой бы ни была окружность, отношение её длины к её диаметру является постоянным числом. Сейчас это число обозначают греческой буквой π. (читается – «пи»)
Как измерить дину окружности?
Можно взять сантиметровую ленту (если нет ленты, можно воспользоваться нитью или полоской бумаги).
Можно прокатить кольцо по ровной поверхности, сделав полный оборот.
Проверьте, верно ли, что отношение длины окружности к диаметру ≈ 3?
Возьмите несколько круглых предметов (тарелка, стакан, игрушечное колесо и др.).
Результаты измерений можно записать в таблицу в тетради.
Закон для более точного вычисления числа π очень сложен. В настоящее время значение π для точных расчётов в строительстве, авиационной или космической промышленности находят при помощи компьютера.
Вспомните, что π – это иррациональное число, которое выражается бесконечной непериодической дробью.
При решении обычных задач используют приближенное значение
иногда используют π ≈ 3
Обозначим длину окружности буквой С, а её диаметр – буквой d, и запишем формулу:
Следовательно, справедливы формулы:
С = πd или С = 2πR
Круг – это часть плоскости, ограниченная окружностью.
С помощью числа π вычисляют площадь круга.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Впишите верный ответ.
Радиус круга равен 5 см. Найдите длину окружности С, площадь круга S.
С = 2πR = 2 ∙ 3,14 ∙ 5 = 31,4 (см).
S = πR 2 = 3,14 ∙ 5 2 = 3,14 ∙ 25 = 78,5 (см 2 ).
Ответ: 31,4 см; 78,5 см.
Тип 2. Множественный выбор
Вычислите площади заштрихованных фигур (размер 1 клетки равен 1 см 2 ).
Из круга вырезали квадрат.
Sкруга = πR 2 = 3,14 ∙ 4 2 = 3,14 ∙ 16 = 50,24 (см 2 ).
Sквадрата = а 2 = 4 2 = 16 (см 2 ).
Sзаштрих = 50,24 – 16 = 34,24 (см 2 ).
Из круга вырезали круг.
S1 = πR 2 = 3,14 ∙ 6 2 = 3,14 ∙ 36 = 113,04 (см 2 ).
S2 = πR 2 = 3,14 ∙ 3 2 = 3,14 ∙ 9 = 28,26 (см 2 ).
Sзаштрих = 113,04 – 28,26 = 84,78 (см 2 ).
📹 Видео
Отношение длины окружности к её диаметру. Площадь круга.Скачать

Длина окружности. Математика 6 класс.Скачать

Площадь круга. Математика 6 класс.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Длина окружности и площадь кругаСкачать

+Как найти длину окружностиСкачать

Окружность и круг, 6 классСкачать

ПЛОЩАДЬ КРУГА. ЛАЙФХАК #math #логика #загадка #математика #геометрияСкачать

6 класс, 3 урок, Длина окружности и площадь кругаСкачать

Геометрия 9 класс (Урок№25 - Решение задач с исп.форм.длины окр.,площади круга и кругового сектора.)Скачать

Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать
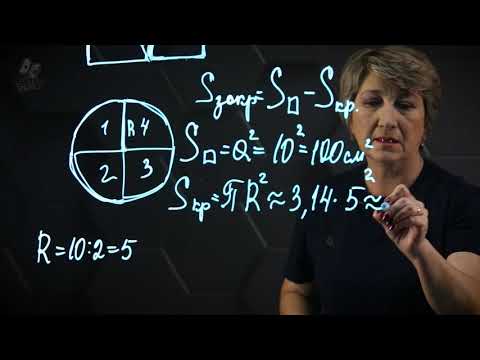
Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

История возникновения формул для площади круга и длины окружности.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать









