Отношение площадей вписанной и описанной окружности квадрата

Квадрат – ромб, у которого все углы прямые.

Квадрат – прямоугольник с равными сторонами.

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Свойства квадрата

Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Описанная окружность

Около квадрата можно описать окружность. Сторона и радиус окружности связаны соотношением:

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Площадь квадрата

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Задание 3 ЕГЭ по математике. Урок 47Скачать

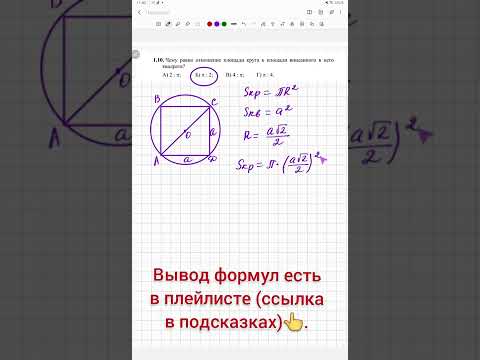
Отношение площадей вписанной и описанной окружности квадрата

Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

Пусть радиус окружности равен R. Тогда сторона описанного вокруг нее квадрата равна 2R, а его площадь, равная квадрату стороны, равна 4R 2 . Диагональ вписанного квадрата также равна 2R, поэтому его площадь, равная половине произведения диагоналей, равна 2R 2 . Следовательно, отношение площади описанного квадрата к площади вписанного равно 2.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как определить площадь квадрата

О чем эта статья:

3 класс, 8 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Найти отношение площади круга к площади вписанного в него квадрата. Геометрия 9 класс. Математика.Скачать

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

S = a × a = a 2 , где S — площадь, a — сторона.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Видео:ЕГЭ Задание 16 Отношение площадей подобных треугольниковСкачать

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

S = 4 × r 2 , где r — это радиус вписанной окружности.

Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

S = 2 × R 2 , где R — это радиус описанной окружности.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Видео:Отношение площадей треугольниковСкачать

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .

Ответ: 4050 мм 2 .

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

🎥 Видео

Найдите отношение площадейСкачать

60. Отношение площадей подобных треугольниковСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Найти площадь квадрата описанного около окружности радиуса 19Скачать

Квадрат в окружности или окружность в квадрате #ShortsСкачать

Площадь круга. Математика 6 класс.Скачать