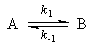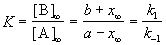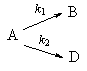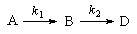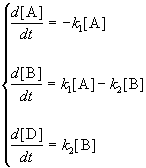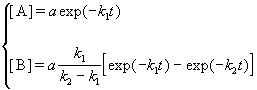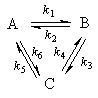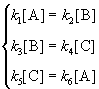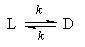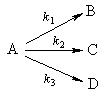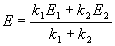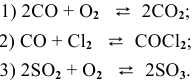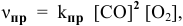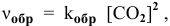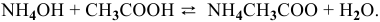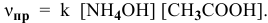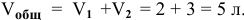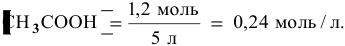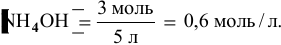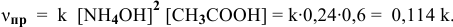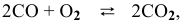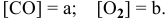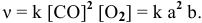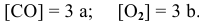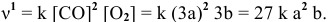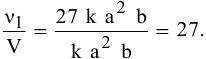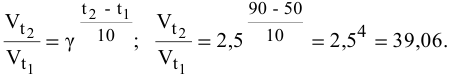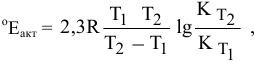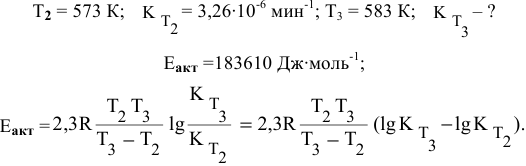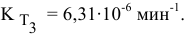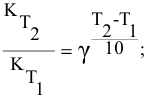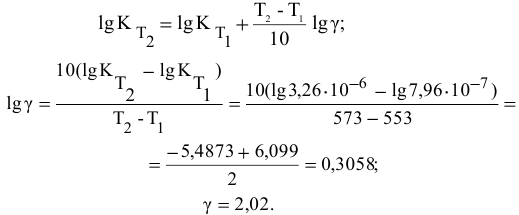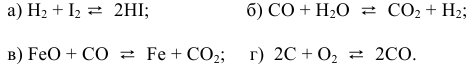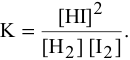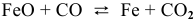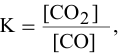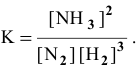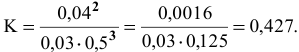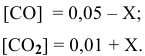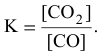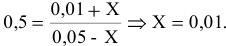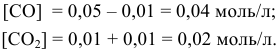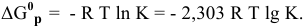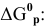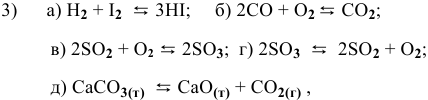Как решается прямая кинетическая задача для параллельных химических реакций

При изучении кинетики сложных реакций, включающих несколько элементарных стадий, используют принцип независимости химических реакций:

Если в системе протекает несколько простых реакций, то каждая из них подчиняется основному постулату химической кинетики независимо от других реакций.

Основные типы сложных реакций мы рассмотрим на примере реакций первого порядка.

1. Обратимые реакции первого порядка:

Закон действующих масс записывается следующим образом:

.

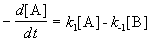
Если начальные концентрации веществ A и B обозначить, соответственно, a и b и ввести степень превращения x ([A] = a — x, [B] = b + x), то кинетическое уравнение приобретает вид:

.

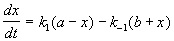
Решение этого уравнения можно выразить через степень превращения, соответствующую достижению равновесия:

или , (5.1)

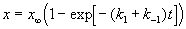
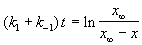
где x определяется условием равенства скоростей прямой и обратной реакций:

, откуда следует: . (5.2)

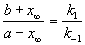
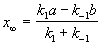
При t наступает равновесие, которое характеризуется константой:

2. Параллельные реакции первого порядка:

Кинетическое уравнение записывается с учетом принципа независимости:

.

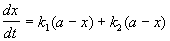
Решение этого уравнения записывается так же, как и для одной реакции первого порядка:

, . (5.3)

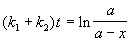
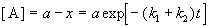
Для параллельных реакций в любой момент времени отношение концентраций продуктов постоянно и определяется константами скорости элементарных стадий:

.

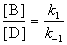
3. Последовательные реакции первого порядка:

Пусть в начальный момент времени есть только вещество A. Применим к этой системе закон действующих масс и принцип независимости химических реакций:

Решение этой системы дает концентрации веществ:

Концентрация промежуточного вещества достигает максимума при

.

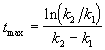
Величина этого максимума определяется отношением констант k₂ / k₁. Если оно велико, т.е. k₂ >> k₁, то промежуточный продукт не успевает накапливаться и его концентрация в любой момент времени мала. В этом случае для анализа кинетических уравнений можно использовать приближенный метод квазистационарных концентраций ( 6).

Пример 5-1. Для обратимой реакции первого порядка

K_равн = 8, а k₁ = 0.4 с -1 . Вычислите время, при котором концентрации веществ A и B станут равными, если начальная концентрация вещества B равна 0.

Решение. Из константы равновесия находим константу скорости обратной реакции:

с -1 .

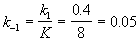
По условию, мы должны найти время, за которое прореагирует ровно половина вещества A. Для этого надо подставить значение x(t) = a/2 в решение кинетического уравнения для обратимых реакций (5.1) и (5.2):

c.

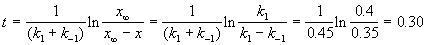
Пример 5-2. В параллельных реакциях первого порядка

выход вещества B равен 63%, а время превращения A на 1/3 равно 7 минутам. Найдите k₁ и k₂.

Решение. Кинетическое уравнение (5.3) для разложения вещества в параллельных реакциях имеет вид уравнения первого порядка, в которое вместо одной константы скорости входит сумма констант скорости отдельных стадий. Следовательно, по аналогии с реакциями первого порядка, по времени превращения A на 1/3 (x(t) = a/3) можно определить сумму констант k₁ + k₂:

мин -1 .

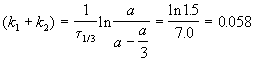
Выход вещества В равен 63%, а вещества D — 37%. Отношение этих выходов равно отношению конечных концентраций веществ B и D, следовательно оно равно отношению соответствующих констант скорости:

.

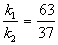
Решая это уравнение совместно с предыдущим, находим: k₁ = 0.037 мин -1 , k₂ = 0.021 мин -1 .

Пример 5-3. Имеется следующее равновесие:

Как связаны между собой константы k₁ — k₆?

Решение основано на принципе детального равновесия:

Если сложная система находится в равновесии, то в каждой из элементарных стадий также соблюдается равновесие.

Это означает, что во всех трех процессах: A B, B C и C A скорости прямой и обратной реакций равны:

Перемножив почленно эти три равенства и поделив левую и правую части на произведение равновесных концентраций [A] . [B]. [C], находим искомое соотношение между константами скорости:

.

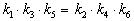
5-1. Нарисуйте графики зависимости концентраций веществ A и B от времени в обратимой реакции A B для двух случаев: 1) k₁ > k_-1; 2) k₁ -1 . Вычислите время, при котором концентрации веществ A и B станут равными, если начальная концентрация вещества B равна 0.(ответ)

5-5. Превращение роданида аммония NH₄SCN в тиомочевину (NH₄)₂CS — обратимая реакция первого порядка. Рассчитайте константы скорости прямой и обратной реакций, используя следующие экспериментальные данные:

t, мин

Доля прореагировавшего NH₄SCN, %

5-6. Один из методов оценки возраста биологических объектов основан на измерении содержания в них оптических изомеров аминокислот. В живых организмах отношение концентраций D- и L-изомеров постоянно ([D]₀ / [L]₀ = a). В мертвых организмах происходит рацемизация:

Чему равен возраст биологического объекта, в котором [D] / [L] = b? Решите задачу в общем виде и для образца, содержащего аспарагиновую кислоту (k = 1.48 . 10 -5 лет -1 , a = 0.07, b = 0.27).(ответ)

5-7. В параллельных реакциях первого порядка

выход вещества B равен 53%, а время превращения A на 1/3 равно 40 c. Найдите k₁ и k₂.(ответ)

5-8. Реакция разложения вещества А может протекать параллельно по трем направлениям:

Концентрации продуктов в смеси через 5 мин после начала реакции были равны: [B] = 3.2 моль/л, [C] = 1.8 моль/л, [D] = 4.0 моль/л. Определите константы скорости k₁ — k₃, если период полураспада вещества А равен 10 мин.(ответ)

5-9. Реакция разложения вещества А может протекать параллельно по трем направлениям:

Концентрации продуктов в смеси через 10 мин после начала реакции были равны: [B] = 1.6 моль/л, [C] = 3.6 моль/л, [D] = 7.8 моль/л. Определите константы скорости k₁ — k₃, если период полураспада вещества А равен 8 мин.(ответ)

5-10. Покажите, что при двух параллельных реакциях

энергия активации суммарной реакции разложения A связана с энергиями активации отдельных стадий следующим образом:

*5-11. В системе идут две параллельные газофазные реакции: А + B C (k₁), A D (k₂). Исходная смесь эквимолекулярна, начальное давление составляет 200 мм рт. ст. При практически полном превращении А при 227 о С Р_С = 10 мм рт.ст., а при 327 о С Р_С = 39 мм рт.ст. Найдите разность энергий активации этих реакций.(ответ)

5-12. На одном графике нарисуйте зависимости концентрации вещества B от времени в системе последовательных реакций A B D для двух случаев: 1) k₁ >> k₂; 2) k₁ > 1; 2) k₂ / k₁

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Задачи с решениями на химическую кинетику и химическое равновесие

Химическая кинетика и химическое равновесие

Задача № 1. Написать математическое выражение скорости прямой и обратной реакций:

Пример 59

Для реакции 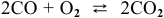согласно закону действия масс выражения скоростей реакции следующие:

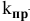
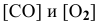
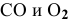
где — константа скорости прямой реакции;

— соответственно концентрации ;

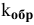
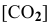
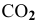
где — константа скорости обратной реакции;

— концентрация .

Задача 43

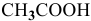
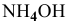
Определить начальную скорость реакции с константой скорости прямой реакции к в растворе, полученном смешением 2 л 0,6 М раствора и 3 л 1 М раствора .

Решение:

Уравнение химической реакции, происходящей в смеси двух растворов, следующее:

Согласно закону действия масс выражение скорости химической реакции

Для определения скорости реакции необходимо знать величину концентраций веществ 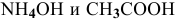в момент их смешения. Для этого определим объем смеси двух растворов:

Зная, что в исходном растворе уксусной кислоты содержится 0,6-2 = = 1,2 моль 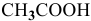, находим ее концентрацию в смеси:

В исходном растворе гидроксида аммония содержится 1-3=3 моль 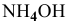, значит, концентрация его в смеси

Определяем начальную скорость реакции:

Задача 44

Как изменится скорость прямой реакции

если давление увеличить в 3 раза?

Решение:

Предположим, что в начальный момент до повышения давления концентрации реагирующих веществ следующие:

Скорость реакции, определяемая по закону действия масс, до повышения давления равна:

Согласно уравнению Менделеева-Клапейрона 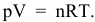Повышение давления в 3 раза приводит к повышению концентрации каждого компонента в 3 раза.

Таким образом, после повышения давления концентрации реагирующих веществ станут равными:

Скорость реакции после повышения давления

Повышение скорости реакции будет следующим:

При повышении давления в 3 раза скорость прямой реакции увеличивается в 27 раз.

Задача 45

Во сколько раз увеличится скорость реакции при увеличении температуры с 50 до 90°С? Температурный коэффициент реакции у равен 2,5.

Решение:

Согласно правилу Вант-Гоффа

Задача 46

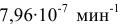
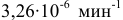
Константа скорости реакции разложения HI равна при 280°С и при 300°С. Определить энергию активации, константу скорости при 310 °C и температурный коэффициент скорости реакции.

Решение:

Воспользуемся формулой, являющейся производной уравнения Аррениуса:

Теперь, зная энергию активации, можно рассчитать константу скорости реакции при 310 °C:

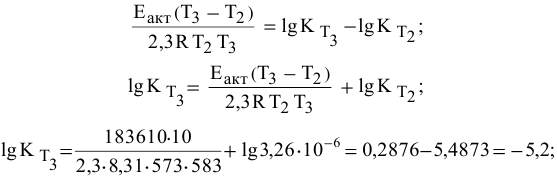
Определяем температурный коэффициент по следующей формуле:

Задача 47

Написать математические выражения констант равновесия следующих реакций:

Решение:

а) Для гомогенной реакции

б) Для гетерогенной реакции

так как концентрации твердых веществ не входят в выражение константы равновесия.

Задача 48

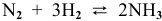
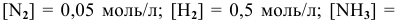
В состоянии равновесия системы при определенной температуре концентрации участвующих в равновесии веществ следующие: =0,04 моль/л. Рассчитать константу равновесия этой реакции.

Решение:

Подставим в выражение константы равновесия значения равновесных концентрации:

Задача 49

Константа равновесия реакции 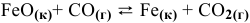при 1000 °C равна 0,5. Исходные концентрации равны соответственно 0,05 моль/л и 0,01 моль/л. Рассчитать их концентрации в состоянии равновесия.

Решение:

Предположим, что в ходе реакции до момента установления состояния химического равновесия концентрация СО уменьшается на X моль/л. Тогда в состоянии химического равновесия концентрации будут следующими:

Математическое выражение константы равновесия данной реакции:

Отсюда находим значение X:

В состоянии равновесия значения концентрации будут следующими:

Задача 50

Для реакции 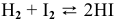рассчитать константу равновесия в стандартных условиях.

Решение:

Между энергией Гиббса и константой равновесия существует следующая взаимосвязь:

Рассчитываем вначале значение

Находим значение константы равновесия реакции в стандартных условиях :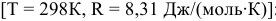

Задача 51

В каком направлении сместится равновесие следующих химических реакций:

если увеличить температуру?

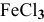
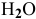
если увеличить концентрацию для реакции а и уменьшить концентрацию для реакции б?

если увеличить давление?

Решение:

Воспользуемся принципом Ле Шателье.

1) Увеличение температуры смещает химическое равновесие в направлении эндотермической реакции, а уменьшение температуры — в направлении экзотермической реакции.

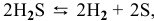
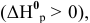
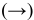
Для реакции являющейся эндотермической увеличение температуры смещает равновесие в сторону прямой реакции .

2) Увеличение концентрации одного из участвующих в равновесии веществ смещает химическое равновесие в сторону реакции, уменьшающей концентрацию этого вещества.

Уменьшение концентрации одного из участвующих в равновесии веществ смещает химическое равновесие в сторону реакции, увеличивающей концентрацию этого вещества.

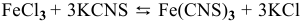
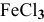
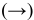
Для реакции увеличение концентрации , являющегося реактивом, смещает равновесие в сторону реакции, уменьшающей его концентрацию, т.е. в прямом направлении .

3) Увеличение давления смещает химическое равновесие в направлении реакции, вызывающей уменьшение объема системы, т.е. в сторону реакции с уменьшением числа газообразных молекул.

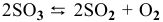
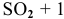
Для реакции увеличение давления смещает равновесие в сторону обратной реакции , так как число молекул исходных веществ (2 молекулы ) меньше, чем число молекул продуктов реакции (2 молекулы молекула , итого 3 молекулы).

Эти задачи взяты со страницы решения задач по неорганической химии:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Практическое занятие 5, 6 «Методы кинетико-термодинамического анализа сложных химических реакций» (4 часа)

Практическое занятие 5, 6 «Методы кинетико-термодинамического анализа сложных химических реакций» (4 часа)

План занятия: Основные типы сложных реакций, кинетика обратимых реакций, кинетика параллельных реакций, кинетика последовательных реакций. Решение задач.

Сложной реакцией называют совокупность одновременно протекающих одностадийных реакций, в результате которых происходит превращение реагентов в продукты. В ходе сложной реакции часто образуются промежуточные вещества, которые подвергаются дальнейшему превращению. Часто — это активные частицы с неспаренными электронами — так называемые радикалы.

Большинство реакций являются сложными и состоят из нескольких элементарных стадий. Все многообразие сложных реакций можно свести к комбинации нескольких типов реакций: обратимые (двусторонние); параллельные; последовательные и др.

При изучении кинетики сложных реакций, включающих несколько элементарных стадий, используют принцип независимости (1.17): если в системе протекает несколько простых реакций, то каждая из них подчиняется основному постулату химической кинетики независимо от других реакций.

Кинетика обратимых реакций

При протекании обратимых химических реакций необходимо учитывать принцип детального равновесия:

при равновесии скорость прямой реакции для каждой стадии равна скорости обратной реакции.

Рассмотрим этот принцип на примере следующего процесса. Пусть превращение А в B происходит как без участия ионов водорода, так и при их участии по схеме:

Для скорости образования вещества В можно записать кинетическое уравнение:

Поскольку при равновесиито естьто константа равновесия реакции (4.1) равна:

Возникает кажущееся противоречие, так как константа равновесия не должна зависеть от концентрации ионов водорода. Парадокс устраняется, если использовать принцип детального равновесия. Согласно этому принципу, при равновесии скорости прямой и обратной реакций для каждого пути в отдельности должны быть равны. Следовательно, при равновесии справедливы равенства:

Тогда из (4.4) и (4.5) получим:

Подставляя k1= Kk2 и k 3= Kk 4 в (4.3) получим тождество K = K и, таким образом, противоречие будет снято.

Простейшими обратимыми реакциями являются изомерные превращения: переход цис-формы в транс-форму, изменение положения кратной связи в насыщенных соединениях, их циклизация-дециклизация, кето-енольная и другие виды таутомерии. Рассмотрим несколько примеров описания кинетики обратимых реакций с использованием принципа детального равновесия.

1. Обратимые реакции первого порядка состоят из прямой и обратной элементарных реакций первого порядка:

Общая скорость реакции равна разности скоростей прямой и обратной реакций: v = v1- v2 . Если начальные концентрации веществ А и В обозначить соответственно а и b, а концентрации в любой момент времени сА = а – х и cВ = b + х, то в дифференциальной форме уравнения кинетики имеют вид:

где х — убыль вещества А или прибыль вещества В к моменту времени t; k1 — константа скорости прямой реакции; k2 — константа скорости обратной реакции.

В момент равновесия скорость обратимой реакции равна нулю. Поэтому k1(a — x) = k2 + x) , откуда(b

где K — константа равновесия данной химической реакции; х∞ — убыль вещества А или прибыль вещества В к моменту равновесия.

Из этого уравнения можно выразить х∞:

Преобразуя уравнение (4.6), получим:

Интегральная форма этого уравнения имеет вид:

Уравнение для обратимой реакции первого порядка имеет такой же вид, как и для необратимой реакции первого порядка, с той лишь разницей, что вместо начальной концентрации фигурирует равновесная концентрация, а константу скорости заменяет сумма констант скоростей прямой и обратной реакции.

Кинетические кривые для обратимых реакций первого порядка приведены на рис. 4.1.

2. Типичным примером обратимой химической реакции, в которой обе реакции второго порядка, является реакция омыления сложного эфира:

Схема такой реакции

Рассмотрим решение задачи для случая, когда продукты реакции до начала реакции в реакционной смеси отсутствуют: cА,0 = cB,0 = а и cC,0 = cD,0 = 0. Аналогично предыдущему пункту уравнение скорости химической реакции можно записать в виде:

При достижении состояния равновесия выполняется следующее условие:

С учетом уравнения (4.13) уравнение скорости химической реакции запишется как:

Полином допускает наличие двух корней квадратного уравнения

Его записывают через произведение вида m(х – х1)(х – х2). Тогда уравнение скорости химической реакции запишется как:

Интегральная форма этого уравнения имеет вид:

Константы скоростей k1 и k2 можно определить из опытного значения кажущейся константы скорости:

Кинетика параллельных реакций

К параллельным реакциям относятся химические превращения, когда взятое для реакции вещество претерпевает изменение одновременно в двух и более направлениях.

К таким реакциям относятся, например, гидролиз сложных эфиров дикарбоновых кислот, или взаимодействие серной кислоты со смесью оксидов металлов. Рассмотрим несколько примеров кинетики таких реакций.

1. Из одного вещества получаются два новых:

Введем обозначения: а — начальная концентрация вещества А, х — изменение концентрации этого вещества к моменту времени t; у — концентрация вещества В; z — концентрация вещества C в момент времени t.

Тогда кинетическое уравнение записывается с учетом принципа независимости (rAv= -1 — v2):

Решение уравнения (4.18) имеет вид:

Откуда концентрация исходного вещества в любой момент времени t равна:

Тогда можно выразить изменение концентрации продуктов реакции:

Интегрирование уравнений (4.23) и (4.24) в пределах от 0 до t и, соответственно, от 0 до y и z дает:

Из уравнений (4.25) и (4.26) следует что, для параллельных реакций в любой момент времени отношение концентраций продуктов постоянно и определяется отношением констант скоростей элементарных стадий:

Кинетические кривые для случая двух параллельных реакций первого порядка приведены на рис. 4.2.

2. Рассмотрим случай, когда параллельные реакции являются реакциями второго порядка.

Такой процесс можно представить общей схемой:

Если обозначить a и b начальные концентрации веществ A и B, то кинетическое уравнение в дифференциальной форме можно представить как:

Интегрирование этого уравнения позволяет оценить сумму констант скоростей:

Отношение концентраций продуктов, как и в первом случае, не зависит от времени и определяется отношением констант скоростей.

Кинетика последовательных реакций

Расчет кинетики последовательных реакций в общем виде довольно сложен, так как если процесс состоит из двух или нескольких последовательных реакций, то кинетика его описывается системой дифференциальных уравнений. Только для более простых реакций с последовательными стадиями первого порядка удается получить аналитические выражения для концентрации веществ в явном виде.

Примером такой простой последовательной реакции может служить гомогенная реакция в закрытой системе с двумя односторонними мономолекулярными элементарными стадиями (первого порядка):

Примерами таких реакций являются, в частности, радиоактивные превращения веществ или нуклеофильные замещения в ароматических соединениях.

Рассмотрим случай, когда константы скорости k1 и k2 двух последовательных стадий различаются не более чем на один порядок и, следовательно, обе стадии являются лимитирующими.

Решим прямую задачу, т. е. найдем зависимость концентрации от времени для всех трех веществ, считая известными механизм реакции и константы скорости обеих стадий:

Пусть в начальный момент времени t = 0 имеется а молей вещества А, а вещества В и С отсутствуют. Если к моменту времени t прореагировало х молей вещества А, то осталось cA = (а – х) молей. Обозначим через у количество В, превратившееся к этому времени в С. Следовательно, вещества В имеется cB = (х – у) молей, а вещества С имеется у молей.

Скорость превращения вещества А можно выразить:

или на основе формальной кинетики:

Интегрирование этого уравнения от 0 до t и от 0 до х приводит к следующим выражениям:

Скорость превращения вещества B описывается уравнениями:

Подставляя значение х из (4.32) в (4.33) и интегрируя полученное уравнение от 0 до t и от 0 до у, получаем:

Вычитая уравнение (4.34) из (4.32), получим:

Зависимость концентрации веществ от времени в системе двух последовательных реакций первого порядка приведена на рис. 4.3.

Как видно из рисунка, изменение концентрации промежуточного вещества во времени представляет собой кривую с максимумом. Величина этого максимума определяется различием в значениях констант:

При решении обратной задачи по кинетическим кривым необходимо определить k1 и k2. Константу скорости k1 легко можно определить на основании уравнения (4.31). Однако определение k2 несколько сложней, так как уравнение (4.35) является транцедентным, из которого в явном виде выразить k2 нельзя. Для расчета k2 лучше воспользоваться уравнениями (4.36) или (4.37), которые решаются численно. Для этого, зная k1, экспериментально определяют максимум концентрации вещества B, а затем рассчитывают k2.

Рассмотрим полезные соотношения между концентрациями В, С и А в случае, если лимитирующей стадией процесса является реакция с константой скорости k1.

Переходное равновесие. Если k2 >> k1, то после длительного промежутка времени выражение (4.35) упрощается:

Поделив уравнение (4.38) на (4.31), получим выражение для так называемого переходного равновесия:

То есть в стационарном состоянии отношение концентрацийвеличина постоянная.

В этом случае отношение концентраций(с учетом k2 >> k1) равно:

Вековое равновесие. Если k2 >> k1, то в уравнении (4.39) можно пренебречь в знаменателе k1, тогда получим уравнение, называемое вековым равновесием:

где t1 и t2 — средние времена жизни; t1/2(1) и t1/ 2(2) — периоды полураспада, соответственно, веществ А и В. В этом случае при t ®∞ сс/а=1.

Примеры решения задач

Пример 1. Реакция изомеризации β-оксикротонового эфира в ацетоуксусный эфир

при 25 °С протекает как в прямом, так и в обратном направлении. Изменение концентрации β-оксикротонового эфира во времени приведено в таблице.

В начальный момент времени ацетоуксусный эфир в системе отсутствовал. После установления равновесия в системе концентрация β-оксикротонового эфира составила 0,078 моль/дм3. Рассчитать константы скоростей прямой и обратной реакций.

Решение. Реакция изомеризации β-оксикротонового эфира в ацетоуксусный эфир относится к реакциям первого порядка.

1. Значения х и х∞, очевидно, можно рассчитать по соотношениям:

где (c0 – х) — концентрация исходного вещества для времени t.

Отсюда х∞ = 0,366 – 0,078 = 0,288 моль/дм3. Рассчитаем значения х∞ – х в разные моменты времени:

2. Сумму констант скоростей прямой и обратной реакции рассчитаем по формуле (4.10):

Рассчитаем k1 + k2 для различных моментов времени t:

Последние значения (k1 + k2) можно отбросить, так как точность расчета в значительной степени зависит от точности измерения концентрации при t®∞. Среднее значение (k1 + k2) = 0,005126 ч–1.

3. Константу равновесия реакции рассчитаем по соотношению (4.7):

4. Значения каждой из скоростей реакции k1 и k2 можно определить, решив систему уравнений:

Пример 2. Реакция взаимодействия гидропероксидов (ROOH) с кетонами представляет собой обратимую химическую реакцию, протекающую по схеме

Константа скорости прямого процесса k1 = 1 · 10–3 дм3/(моль с), константа равновесия K=

k1/k2 = 8 дм3/моль. Вычислить константу скорости обратной реакции и концентрации веществ А, В и С к моменту равновесия, если cA,0 = cB,0 = 0,02моль/дм3, а C c,0 =0 .

Решение. Значение константы скорости обратной реакции вычислим как

В момент равновесия

Это уравнение преобразуется к виду:

Решением этого квадратного уравнения является два корня: x∞ 1= 0,00246 моль/дм3 и x∞2 = 0,163 моль/дм3. Физический смысл имеет только первый корень.

Концентрации веществ A и B к моменту равновесия станут равны 0,0175 моль/дм3, а концентрация вещества C — 0,00246 моль/дм3.

Пример 3. Уксусная кислота при температуре 700 °С разлагается одновременно по двум направлениям:

Период полураспада уксусной кислоты не зависит от начальной концентрации и равен 0,087 с. Отношение числа молей образовавшихся метана и кетена в любой момент времени равно 0,8. Рассчитать значение суммарной константы скорости и значения констант скоростей каждой из реакций.

1. Определим порядок реакции разложения уксусной кислоты и суммарную константу скорости. Так как период полураспада не зависит от начальной концентрации, то это означает, что реакция разложения уксусной кислоты имеет порядок реакции равный единице. Общую

константу скорости можно рассчитать, исходя из времени полуреакции:

2. Для параллельных реакций справедливо соотношение:

3. Зная сумму констант и их отношение, рассчитаем каждую из констант:

Пример 4. Разложение оксида азота (II) при 1300 К протекает по двум параллельным реакциям:

Начальная концентрация оксида азота (II) равна 4 моль/дм3. Через 0,02 с она изменяется на 77,85 %. Отношение концентраций N2 и N2O в любой момент времени равно 1,4. Рассчитать значения констант скоростей, считая, что этот процесс является реакцией второго порядка.

Решение. По условию задачи через 0,02 с разложится 4×0,7785 = 3,114 моль/дм3 оксида азота (II), а останется (4 – 3,114) = 0,886 молей.

Кинетическое уравнение для разложения оксида азота (II) при протекании параллельных химических реакций в случае реакции второго порядка имеет вид:

Это уравнение позволяет рассчитать сумму констант скоростей:

Для параллельных химических реакций отношение концентраций продуктов реакции в любой момент времени равно отношению констант скоростей:

k2 = 18,3 дм3/моль с; k1 = 25,6 дм3/моль с.

Задачи для самостоятельного решения

1. Цис-транс-изомеризация стильбена (1,2-дифенилэтилена) — обратимая реакция первого порядка. Рассчитайте значения средних констант скоростей прямой и обратной реакций, используя следующие экспериментальные данные:

2. Реакция взаимодействия этанола с соляной кислотой

протекает в органическом растворителе, содержащем 80 % этанола и отвечает обратимой реакции первого порядка типа Экспериментально установлено, как изменяется концентрация HCl во времени при температуре 118 °С.

Определите численные значения констант скоростей k1 и k2.

3. Кинетика реакции этерификации этанола муравьиной кислотой

отвечает реакции первого порядка в обоих направлениях (изучение проводили при большом избытке этанола и воды). При температуре 25 °С константы скорости реакций, соответственно, равны: k1 = 1,85 · 10–3 мин–1, k2 = 1,76 · 10–3 мин–1. Начальная концентрация муравьиной кислоты равна 0,1 М. Рассчитайте процентное содержание образующегося продукта (этилформиата) при достижении равновесия и вычислите время, необходимое для протекания реакции этерификации на 80 % от равновесного состояния.

4. Образец радиоактивного урана массой 100 г распадается по схеме

(над стрелкой указаны периоды полураспада). Рассчитайте массы нептуния и плутония через: а) 20 мин; б) 20 суток после начала распада.

5. Реакция превращения γ-оксимасляной кислоты в лактон представляет собой обратимую реакцию первого порядка как в прямом, так и в обратном направлениях (концентрация воды постоянная):

Начальная концентрация γ-оксимасляной кислоты была равна 0,1823 моль/дм3. Ниже приведены данные изменения концентрации лактона во времени:

Рассчитайте константу равновесия данной реакции и значения констант скоростей прямой и обратной реакций.

протекает при 0 °С и может быть представлена общей схемой:

Начальная концентрация вещества А была равна 0,0348 моль/дм3; константы скоростей равны: k1 = 1,78 · 10–3 с–1 и k2 = 5,80 · 10–5 с–1. Рассчитайте концентрации всех участников реакции к моменту времени t = 500 с. Вычислите время достижения максимума концентрации промежуточного вещества В.

7. Реакция взаимодействия уксусной кислоты (c0 = 1.00 моль/дм3) с этиловым спиртом проводилась в среде 40%-го этилового спирта. Образованию этилацетата соответствует уравнение реакции:

Кинетику этой реакции изучали, титруя 1,00 см3 раствора 0,0612 моль/дм3 NaOH. Получены следующие результаты:

Рассчитайте константу равновесия и константы скоростей прямой и обратной реакций.

была измерена доля распавшегося HI при различных временах нагревания:

Начальная концентрация иодистого водорода была равна 0,0446 моль/дм3. Рассчитайте константу равновесия данного процесса и значения констант скоростей прямого и обратного процессов.

9. Реакция разложения изопропилового спирта протекает в присутствии катализатора (триоксида ванадия) при 588 К по следующей схеме:

Концентрации веществ, измеренные через 4,3 с после начала опыта, оказались следующими: c (C3H7OH) = 0,0274 моль/дм3; c (C3H6O) = 0,0075 моль/дм3; c (C3H6) = 0,081 моль/дм3; c (C3H8) = 0,017 моль/дм3. Рассчитайте константу скорости каждой из стадий реакции.

10. Образование этилового эфира муравьиной кислоты при 303 К протекает по уравнению реакции первого порядка (спирт взят в большом избытке):

Константа равновесия этой реакции равна 1,05. За изменением концентрации кислоты следили путем титрования проб одинакового объема:

Концентрация продукта реакции в начальный момент времени равна нулю. Вычислите численные значения констант скоростей k1 и k2 в этом растворе.

11. Превращение роданида аммония в тиомочевину — обратимая реакция первого порядка

Экспериментально оценивалась доля NH4 SCN (a), прореагировавшего к моменту времени t. Рассчитайте скорости прямой и обратной реакций, используя следующие экспериментальные данные:

12. В газовой фазе протекает реакция

Для опыта были взяты 2 моля газа А. Константы скоростей отдельных стадий реакции соответственно равны: k1 = 18 · 10–2 с–1 и k2 = 2 · 10–3 с–1. Рассчитайте количества молей каждого газа к моменту времени t = 180 с. Какого из веществ в газовой смеси будет больше к этому моменту времени?

13. Реакция разложения вещества А может проходить параллельно по трем направлениям:

Начальная концентрация вещества А была равна 5 моль/дм3. Через десять минут от начала реакции концентрация вещества B стала равной 1 моль/дм3, а соотношение концентраций продуктов C и D — С : D = 6 : 1. Период полураспада вещества А равен 8 мин. Определите константы скоростей k1, k2 и k3.

14. Муравьиная кислота на окисных катализаторах разлагается в соответствии со схемой:

В одном из опытов за 15,4 c выход CО2 составил 77,5 % от теоретического, а СО — 2,6 %. Вычислите константы скоростей дегидратации и дегидрирования муравьиной кислоты.

15. В газовой фазе протекает реакция

Для опыта были взяты 5 молей газа А. Константы скоростей отдельных стадий реакции соответственно равны: k1 = 18 · 10–2 с–1 и k2 = 2 · 10–3 с–1. Рассчитайте, к какому моменту времени концентрация вещества В будет максимальна. Какова будет концентрация веществ А и С к этому моменту времени?

16. Разложение закиси азота при 1300 К протекает по двум параллельным реакциям:

Начальная концентрация закиси азота равна 4 моль/дм3. Сколько азота и закиси азота образуется через 0,1 с, если константы скорости параллельных реакций имеют следующие значения: k1 = 25,7 дм3/(моль с) и k2 = 18,27 дм3/(моль с)?

17. В системе протекают две параллельные реакции:

Отношение k1 / k 2= 5. Начальные концентрации веществ В и С одинаковы. К моменту времени t прореагировало 50 % вещества В. Какая часть вещества С прореагировала к этому времени?

18. Термическое разложение циклобутанона приводит к образованию смеси продуктов, согласно реакции

Начальное количество циклобутанона равно 10 моль. При температуре 383 К отношение концентраций С2Н4 и С3Н6 в любой момент времени протекания процесса оставалось постоянным и равным 125. Через 50 с от начала реакции в газовой смеси содержалось 0,7 молей СО. Рассчитайте значения констант скоростей обоих процессов.

19. Реакция этерификации этилового спирта уксусной кислотой

является обратимой химической реакцией второго порядка в обоих направлениях. При определенной температуре для начальных концентраций обоих реагентов, равных 1 моль/дм3, было установлено, что концентрация образующегося эфира равна 0,25 моль/дм3 через t = 65 сут и 2/3 моль/дм3 — при установлении равновесия (t ® ∞). Рассчитайте константу равновесия данного процесса и значения констант скоростей прямого и обратного процессов.

20. Константа равновесия реакции

при температуре 2400 К и p = 1,013 · 105 Па равна 398,4, а константа скорости k1 = 6,03×109 дм3/(моль с). Рассчитайте константу скорости k2 данной реакции и концентрацию всех компонентов к моменту времени t = 200 с, если начальное давление NO равно 2,026 × 103 Па.

21. Реакция взаимодействия гидропероксидов (ROOH) с кетонами представляет собой обратимую химическую реакцию, протекающую по схеме

Константа скорости прямого процесса k1 = 1 · 10–3 дм3/(моль с), константа равновесия K = 7 дм3/моль. Вычислите концентрацию веществ А, В и С через 10 ч от начала реакции и к моменту равновесия, если c A 0= c B 0=0,03 моль/дм3, а c C0 = 0 .

22. С помощью масс-спектрометрического метода изучалась кинетика реакций:

Было найдено, что отношение констант скоростей отвечает соотношению k1 : k2 : k3 = 0,62 : 0,11 : 0,27. Оцените отношение концентраций продуктов реакции ко времени t.

23. Константы скоростей прямой и обратной реакций соответственно равны 2 с–1 и 30 с–1. Исходные концентрации веществ А и В взяты равными 0,04 моль/дм3. Найдите концентрации этих веществ через 0,04 с.

при температуре Т протекают параллельно. Вычислите константы скорости каждой реакции, если концентрации, измеренные в одном из опытов продолжительностью 240 мин, следующие (этилен взят в избытке):

📹 Видео

Скорость химических реакций. 9 класс.Скачать

Задачи на скорость реакции в зависимости от концентрации реагентовСкачать

Кинетический анализ сложных реакцийСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

ЛЕКЦИЯ №5 || Химическая кинетика || Обратимые реакции, параллельные реакции (начало)Скачать

Скорость химической реакции. Практическая часть. 10 класс.Скачать

Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Химия ПростоСкачать

Химическая кинетика. Скорость химической реакции | ХимияСкачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Составляем кинетические уравненияСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Химия - решение типовых задач по теме "Химическая кинетика и химическое равновесие"Скачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать

задачи на порядок хим реакцииСкачать