- 1.Площадь прямоугольника
- Площадь прямоугольника со сторонами a и b
- 2.Площадь параллелограмма
- 3.Площадь треугольника
- 4.Площадь круга
- 5.Площадь подобных фигур
- 6.Площадь трапеции
- Репетитор: Васильев Алексей Александрович
- 7.Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Формулы площадей фигур
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Формулы площади квадрата
- Формула площади квадрата по длине стороны
- Формула площади квадрата по длине диагонали
- Формула площади прямоугольника
- Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
- Формула площади параллелограмма по двум сторонам и углу между ними
- Формула площади параллелограмма по двум диагоналям и углу между ними
- Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
- Формула площади ромба по длине стороны и углу
- Формула площади ромба по длинам его диагоналей
- Формулы площади трапеции
- Формула Герона для трапеции
- Формула площади трапеции по длине основ и высоте
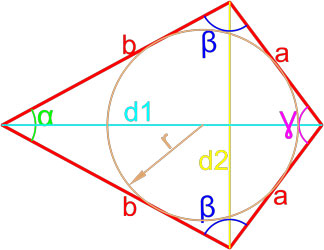
- Формулы площади дельтоида
- Формула площади дельтоида по двум неравным сторонам и углу между ними
- Формула площади дельтоида по равным сторонам и углу между ними
- Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
- Формула площади дельтоида по двум диагоналям
- Формулы площади произвольного выпуклого четырехугольника
- Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
- Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
- Формула площади вписанного четырехугольника (формула Брахмагупты)
- Формула площади четырехугольника с вписанной окружностью
- Формула площади четырехугольника с вписанной и описанной окружностями
- Формулы площади круга
- Формула площади круга через радиус
- Формула площади круга через диаметр
- Площадь сегмента круга
- Площадь кругового сегмента через угол в градусах.
- Площадь кругового сегмента через угол в радианах.
- Формула площади эллипса
- 51. Планиметрия Читать 0 мин.
- 51.506. Отношения
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

1.Площадь прямоугольника
Отношение площадей двух прямоугольников с общим основанием равно отношению двух других их сторон.
Доказательство.
Пусть ABCD и ABC’D’ два прямоугольника с общим основанием АВ. (Рис.1) Разобьем сторону AD на n частей. Тогда длина AD’ составит:
где m — число целых делений на отрезке AD’. Т.е. длина отрезка AD’ будет заключена между m и m+1 частей.
Разделив все части неравенства на AD, получим:
Тогда и площадь прямоугольника AD’C’B также будет заключена в пределах:
где S — площадь прямоугольника ABCD.
Разделив все части неравенства на S, получим:
Отсюда следует, что два соотношения площадей и сторон заключены между двумя соотношениями, т.е.:
При достаточно большом n можно сделать вывод, что они равны.

Рис.1 Площадь прямоугольника.
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Площадь прямоугольника со сторонами a и b
Теперь рассчитаем площадь прямоугольника. Возьмем квадрат, который имеет площадь равную единице. И сравним его с прямоугольником, у которого основание равно единице, а другая сторона равна а. Получим:
Теперь сравним прямоугольник со сторонами а и 1 с прямоугольником со сторонами а и b. Получим:
Перемножив два равенства между собой, получим:

Видео:Площадь параллелограмма, треугольника, трапецииСкачать

2.Площадь параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Пусть дан параллелограмм ABCD (Рис.2). Проведем высоты AF, BP и СE на стороны AD и BC. Тогда треугольники AFB и СED равны по первому признаку равенства треугольников. AF = СE, т.к. они являются перпендикулярами между параллельными прямыми. AB = CD, т.к. ABCD — параллелограмм. Углы при вершинах А и С равны, как соответственные углы при параллельных прямых.
Следовательно площадь параллелограмма равна:
Т.е. площадь параллелограмма равна произведению основания на высоту, проведенную к нему.

Рис.2 Площадь параллелограмма.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

3.Площадь треугольника
Пусть дан треугольник АВС. (Рис.3) Достроим его до параллелограмма. Тогда площадь треугольника ABC будет равна половине площади параллелограмма ABEC. Т.е.:
Т.е. площадь треугольника равна половине произведения его стороны на высоту, опущенную к ней. Или площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Запишем еще две формулы для радиусов вписанной и описанной окружностей треугольника.
R — радиус описанной окружности
r — радиус вписанной окружности
S — площадь треугольника
a,b,c — стороны треугольника

Рис.3 Площадь треугольника.
Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

4.Площадь круга
Кругом называется геометрическая фигура, которая состоит из множества точек, расстояние от которых до данной точки не превосходит определенной величины, называемой радиусом. Где данная точка это центр круга.
Площадь круга равна половине произведения его радиуса и длины окружности.
Доказательство. Пусть АО = R радиус круга. Построим два многоугольника. Один вписанный в круг, а другой описанный около круга. Их площадь обозначим Sоп и Sвп. Тогда их площади будут равны:
Отсюда можно сделать вывод, что при достаточно большом числе n, площадь круга будет равняться половине произведения длины окружности на радиус, т.к. cos α будет стремиться к единице.

Рис.4 Площадь круга.
Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

5.Площадь подобных фигур
Пусть даны две побные фигуры G и G’ (Рис.5). Коэффициент подобия равен k. Разобьем фигуры на треугольники. Тогда площадь каждой фигуры будет равна сумме площадей треугольников, т.е.:
Отсюда можно сделать вывод, что отношение площадей подобных фигур равно квадрату их коэффициента подобия.

Рис.5 Соотношение между углами и сторонами в треугольнике.
Видео:Площадь параллелограмма треугольника и трапецииСкачать

6.Площадь трапеции
Пусть дана трапеция ABCD (Рис.6). Проведем диагональ АС. Получим два треугольника АВС и АСD. Проведем высоты СЕ и АF. Тогда площадь трапеции будет равна сумме площадей треугольников АВС и ACD, т.е.:
Отсюда можно сделать вывод, что площадь трапеции равна произведению полусуммы ее оснований на высоту.

Рис.6 Площадь трапеции.
Репетитор: Васильев Алексей Александрович
Предметы: математика, физика, информатика, экономика, программирование.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

7.Пример 1
Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.
Доказательство:
Пусть дан прямоугольный треугольник АВС. Построим квадраты ABED, ACPK на катетах АВ, АС и квадрат ВСRF на гипотенузе ВС (Рис.7). Тогда площади этих квадратов будут равны:
По теореме Пифагора нам известно, что квадрат гипотенузы равен сумме квадратов катетов, или:
BC 2 = AB 2 + AC 2
Подставим сюда выше записанные выражения и получим:
Отсюда можно сделать вывод, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рис.7 Задача. Докажите, что сумма площадей квадратов.
Пример 2
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.
Решение:
Запишем формулы площадей прямоугольника и параллелограмма:
S1 = AB * AD * sin α — площадь параллелограмма.
Подставим эти выражения в соотношение S2 = 2 S1:
Следовательно, угол α = 30°.
Рис.8 Задача. Параллелограмм и прямоугольник имеют одинаковые стороны.
Пример 3
Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 36 см и 64 см.
Решение:
Пусть дан прямоугольный треугольник ABC. AD — высота, опущенная на гипотенузу ВС. BD = 36 см, DC = 64 см (Рис.9).
По теореме Пифагора составим следующие соотношения:
АВ 2 = BD 2 + AD 2 — из треугольника АВD.
АC 2 = DC 2 + AD 2 — из треугольника АDC.
Первое и второе соотношение решим относительно AD 2 и приравняем их.
АВ 2 — BD 2 = АC 2 — DC 2
Учитывая, что АВС тоже прямоугольный треугольник и BC 2 = AB 2 + АC 2 , перепишем:
АВ 2 — BD 2 = BC 2 — AB 2 — DC 2
2 АВ 2 = BD 2 + BC 2 — DC 2
2 АВ 2 = 36 2 + 100 2 — 64 2
АВ 2 = 3600 или АВ = 60 см.
Рис.9 Задача. Найдите площадь прямоугольного треугольника.
Из прямоугольного треугольника АВС: 100 2 = 60 2 + АС 2 . Откуда, АС = 80 см. Следовательно, площадь треугольника АВС равна:
SABC = AB * AC / 2 = 60 * 80 / 2 = 2400 см 2 .
Пример 4
Найдите радиус r вписанной и радиус R описанной окружностей для равнобедренного треугольника с основанием 6 см и боковой стороной 5 см.
Решение:
Пусть дан равнобедренный треугольник ABC. АВ = ВС = 5 см, АС = 6 см. АО = R — радиус описанной окружности, ОЕ = r — радиус вписанной окружности (Рис.10).
По теореме Пифагора составим следующее соотношение:
АВ 2 = АЕ 2 + ВЕ 2 — из треугольника АВЕ.
ВЕ 2 = АВ 2 — АЕ 2
ВЕ 2 = 5 2 — 3 2 = 16. Откуда ВЕ = 4 см.
Найдем площадь треугольника АВС по формуле S = AE * BE.
S = 3 * 4 = 12 см 2
Теперь рассчитаем радиусы описанной и вписанной окружностей:
R = АС * АВ 2 / 4S = 6 * 5 2 / (4*12) = 150 / 48 = 3.125 см.
r = 2S / (2 AB + AC) = 2 * 12 / (2*5 + 6) = 24 / 16 = 1.5 см.
Рис.10 Задача. Найдите радиус r вписанной.
Пример 5
Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна 8 
Решение:
Пусть дан треугольник ABC. ВЕ = 8 
Так как прямая FD перпендикулярна высоте ВЕ, то она параллельна основанию АС. А следовательно, ∠BAE = ∠BFO, а ∠BСE = ∠BDO. Таким образом, треугольники АВС и FBD подобны.
Отсюда следует, что АC = k FD, BE = k BO.
Найдем площадь треугольников S1 = SFBD и SАВС.
SABC = AC * BE / 2 или SABC = k 2 FD * BO / 2
k 2 FD * BO / 2 = 2 * FD * BO / 2
Отсюда, k 2 = 2, k =
Следовательно, BO = BE / k = 8 

Рис.11 Задача. Прямая, перпендикулярная высоте треугольника.
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

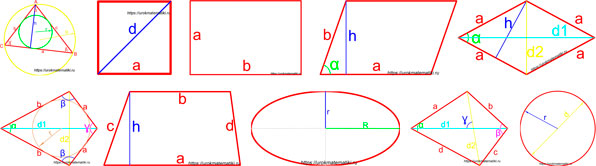
Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Видео:Геометрия 8 класс (Урок№9 - Площадь параллелограмма.)Скачать

Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
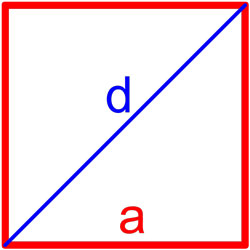
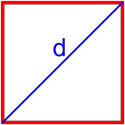
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Видео:Отношение площадей треугольников с равным угломСкачать
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Видео:Отношение площадейСкачать
Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
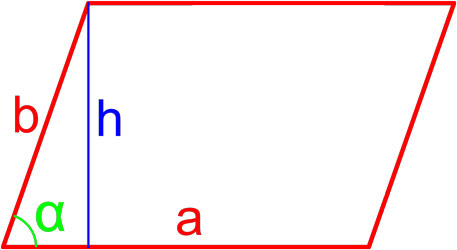
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
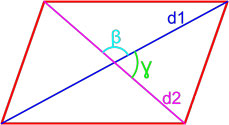
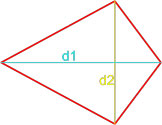
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

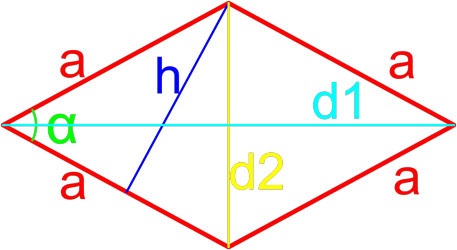
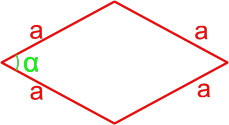
Формулы площади ромба
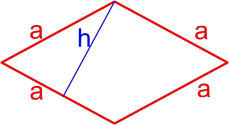
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
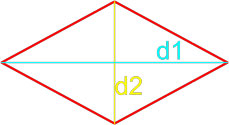
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Видео:Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

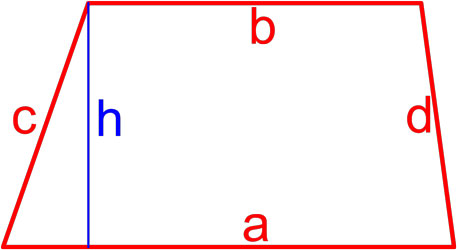
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
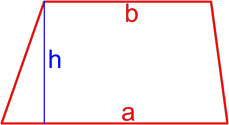
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

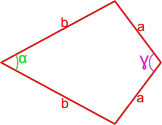
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
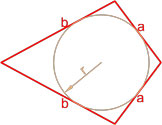
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Видео:Все формулы площади параллелограмма 🔥 #умскул_профильнаяматематика #никитасалливан #егэпрофильСкачать

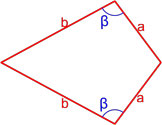
Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
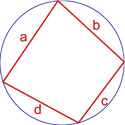
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
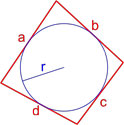
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
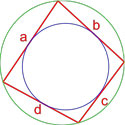
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Видео:ЕГЭ Задание 16 Отношение площадейСкачать

Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
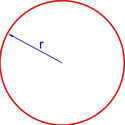
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Видео:Площади треугольников с равным углом.Скачать

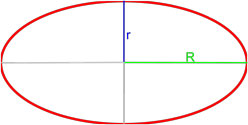
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
51. Планиметрия  Читать 0 мин.
Читать 0 мин.
51.506. Отношения
Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.
ОТНОШЕНИЯ ОТРЕЗКОВ:
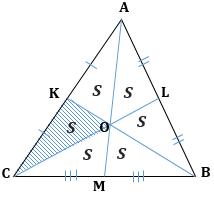
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.
2. Средняя линия треугольника равна половине основания: $MN = fracBC$
3. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна ее половине $CM = fracAB$
4. Диагонали параллелограмма точкой пересечения делятся пополам.
Произвольный параллелограмм или ромб:
Прямоугольник или квадрат:
ОТНОШЕНИЯ ПЛОЩАДЕЙ:
1. Медиана разбивает треугольник на два равновеликих (по площади) треугольника: $S_ = S_ = S$
2. Треугольник делится тремя медианами на шесть равновеликих треугольников:
3. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна $fracS$
ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:
Площади подобных фигур относятся как квадрат коэффициента подобия.
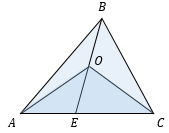
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.
Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.































 Читать 0 мин.
Читать 0 мин.