Отношение параллельные прямые на множестве всех прямых на плоскости (2 видео)

Отношение параллельные прямые на множестве всех прямых на плоскости

Введение в теорию множеств и комбинаторику

Сведения из теории

Пусть даны два множества А и В . Например, множество А – множество флаконов духов ( 10 штук ) и множество В – книги ( 10 штук ).
С помощью множеств А и В мы можем составить множество подарков (100 вариантов), состоящих из двух предметов – духи и книга.

Каждый подарок можно назвать парой. Причем в этом случае не важно, какой из этих предметов первый, а какой второй. Если же мы хотим оформить документально наличие подарков и их содержание, то составляем таблицу, в которой содержится наименование подарка и содержание подарка, причем название предметов обычно одинаковое. Например, первым идет название книги, вторым – название духов. Итак, мы теперь говорим о паре, в которой существует порядок следования компонент: на первом месте название книги, на втором – название духов. В этом случае говорят об упорядоченной паре.

Пусть теперь даны произвольные множества А и В (непустые). Мы можем говорить об упорядоченных парах элементов множеств А и В таких , у которых первая компонента берется из множества А , а вторая – из множества В . Такие пары будем обозначать символом ( х; у ), причем х А , у В , на первую компоненту х не накладывается никаких ограничений, кроме принадлежности множеству А , на вторую компоненту у не накладывается никаких ограничений, кроме принадлежности множеству В . Множество упорядоченных пар ( х; у ), где х А , у В называют декартовым произведением множеств А и В и обозначают символом А В . Другими словами,

А В = < d| d = ( х; у ), х А , у В >.

Аналогично: А В С = < d | d = ( х; у; z ), х А, у В, z С > – декартово произведение трех множеств А, В и С. < d | d = ( , , . ), y i А i , i = 1, 2. , п > – декартово произведение n множеств Ясно, если множество А и В конечны и
| А | = n , | В | = m , то А В тоже конечное, причем | А В | = n m .

Если хотя бы одно из множеств бесконечно, то декартово произведение А В тоже бесконечное.

В частности, можно говорить о декартовом произведении множества А на себя, т. е. А А . Декартово произведение множества А на себя называют декартовым квадратом множества А и обозначают символом А 2 . Другими словами,

А 2 = <d | d = (х; у), х А, у А> . Например, если А = , то

Непустое подмножество декартова произведения множеств А и В называется бинарным соответствием из множества А в множество В. Например, если А = , В = , то D = будет бинарным соответствием из множества А в множество В , т. к. D А В и D Ø.

Значит, для данных множеств А и В бинарное соответствие может быть не одно, т. к. непустых подмножеств множества А В может быть не одно. Сколько непустых подмножеств Y множества А В , столько и различных бинарных соответствий из множества А в множество В .

Если D – бинарное соответствие из множества А в множество В , то А называют множеством исхода, а В – множество прибытия данного бинарного соответствия. Если пары ( х; у ) D, то элемент х из множества А называется точкой исхода, а элемент у из множества В – точкой прибытия в данном бинарном соответствии D . У каждой точки исхода должна быть хотя бы одна точка прибытия. Для каждой точки прибытия должна быть хотя бы одна точка исхода. Итак, не каждый элемент множества А обязан быть точкой исхода и не каждый элемент множества В обязан быть точкой прибытия данного бинарного соответствия D .

Множество точек исхода данного бинарного соответствия D из множества А в множество В называется проекцией бинарного соответствия D на множество А и обозначается символом рr А D . Множество точек прибытия соответствия D называется проекцией бинарного соответствия D на множество В и обозначается символом рr В D .

Итак, рr А D А, рr А D Ø;

рr В D В, рr В D Ø.

В предыдущем примере рr А D = , рr В D = .

Очень часто факт принадлежности пары ( х; у ) бинарному соответствию D обозначают символом хDу и читают: элемент х соответствует элементу у согласно соответствию D . В нашем примере: элементу 1 соответствует элемент а и соответствует элемент с , элементу 2 нет соответствующего элемента, элемент 3 соответствует элементу с . В итоге можно записать: 1D b; 1Dс; 3Dс.

Так как бинарное соответствие D есть подмножество множества А В , то можно говорить о дополнении множества D до множества А В или о . А В , поэтому тоже бинарное соответствие из множества А в множество В . Оно называется соответствием, противоположным к соответствию D .

Итак, ( х; у) , если ( х; у) D . Другими словами, х у , если х не соответствует элементу у согласно соответствия D . В нашем примере = .

Бинарные соответствия целесообразно описывать и представлять себе, основываясь на “геометрической интуиции”, используя так называемые графики. Как мы увидим, привычные уже со школы и столь важные для анализа задание и представление функций с помощью графиков вполне отвечает смыслу графика бинарного соответствия.

Пусть А и В – конечные множества, и пусть D А В – какое-нибудь бинарное соответствие из А в В .

Пусть, для определенности,

А = , В= , и пусть при этом D = <(1; a ), (1; c ),
(2; b ), (2; d ), (4; a ), (5; c )>. Соответствие D можно однозначно и обозримо описать таблицей с двумя входами, так как это показано на рис. 10 для приведенного выше примера:

На горизонтальной оси (оси для элементов множества А ) отмечают столько точек, сколько элементов в множестве А, а на вертикальной оси – столько точек, сколько элементов в множестве B , не занимая вершину угла. Заметим, что расстояния между отмеченными точками необязательно должны быть одинаковыми. Каждой отмечаемой точке на горизонтальной оси приписываем имя элемента множества А , а на вертикальной оси – имя элементов множества B . Так как порядок следования элементов в множестве не существен, то обозначения точек на осях неоднозначно. Из каждой отмеченной точки х А горизонтальной оси восстанавливаем перпендикуляры, из каждой точки у B , отмеченной на вертикальной оси, проводим горизонтали и жирными точками отмечаем пересечения, которые отвечают парам ( х; y ), принадлежащих соответствию D . Множество, отмеченных таким образом точек М(х; у ), образуют так называемый график бинарного соответствия D .

Пусть D = . График такого бинарного соответствия D состоит из трех точек (рис. 11.):

Зная график некоторого бинарного соответствия, мы можем записать это соответствие с помощью пар и указать его множества исхода и прибытия.

Например, дан график некоторого бинарного соответствия

График состоит из четырех точек. Значит, бинарное соответствие состоит из 4-х пар. Множество исхода А = . Множество прибытия B = .

В случае бесконечных множеств А и B нет возможности выписать график-таблицу какого-либо соответствия. B этом случае принято фактически приводить лишь какую-то конечную часть графика, оставляя фантазии читателя “представить” себе весь график.

Граф бинарного соответствия представляет собой чертеж, состоящий из точек, соединенных стрелками. Для построения графа бинарного соответствиями должны быть отмечены точками все элементы множеств А и B (обычно по вертикали параллельно друг другу), обозначенные соответствующими символами.

B предыдущем примере:

Если ( х; у ) D , то находим точку с символом х и от нее проведем стрелку (обычно по дуге) к точке с символом у . Для предыдущего примера:

Полученная картинка, состоящая из точек и стрелок, называется графом бинарного соответствия.

Зная граф бинарного соответствия D , мы сможем написать это соответствие с помощью пар.

Например, дан граф (рис. 13):

Соответствие D = – бинарное соответствие из множества А = в множество B = < ; *; □; О>. Заметим, если множество исхода А или множество прибытия B бесконечны и бинарное соответствие D из множества А в множество B тоже бесконечно, то можно говорить только о части графа этого соответствия.

Можно говорить о бинарном соответствии D из множества А в это же множество А . Такие бинарные соответствия называются бинарными отношениями на множестве А . Итак, бинарными отношениями на множестве А называется непустое подмножество декартового квадрата множества А . Например, А = .

А 2 = < d | d = (х; у), х, у А >, т. е. | А 2 | = 16.

Любое непустое подмножество множества А 2 (а таких подмножеств для нашего примера 2 16 -1) будет бинарным отношением на множестве А . Например, D = . При этом мы можем записать 1D1,2D2, 4DЗ, 4D1, 4D4 и т. д.

Тогда = <( d |d = (х; у), ( х; у) D, х А, у А > –противоположное отношение.

Кроме того, вводится понятие обратного отношения D -1 :

Другими словами, хD -1 у , если уD х : элемент х находится в отношении D — 1 с элементом у , если у находится в отношении D с элементом х . Например, пусть А = , D = .

Тогда =, D -1 = <( b; а ),
( а; а ), (b; с )>. Так как бинарное отношение есть частный случай бинарного соответствия, то для него можно говорить и о графике, и о графе. Причем, при построении графика никаких особенностей нет, а при построении графа применяют в целях удобства некоторые изменения. Именно точки, соответствующие элементам множества А, отмечают по кругу. Например, путь А = . Тогда граф отношения D на множестве А будет состоять из точек, стрелок и петлей. Например, путь D = .

Бинарное отношение D на множестве А может иметь ниже-названные свойства:

1. Рефлексивность : х А: хD х.

Другими словами, каждый элемент х из множества А находится в отношении D с самим собой.

Например, А – множество людей на Земле. Отношение D – «быть другом», т.е. хDу тогда и только тогда, когда человек х друг человека у . Это отношение рефлексивно, т. к. каждый человек – друг самому себе.

Пусть А – множество людей на Земле. Отношение D – «быть сыном», т.е. хDу тогда и только тогда, когда человек х сын человека у . Это отношение не является рефлексивным, т. к. можно найти человека х , который не является сыном самому себе.

2. Симметричность: хDу = > уDх .

Другими словами, если элемент х из множества А находится в отношении D с элементом у , то и элемент у находится в отношении D с элементом х .

Например: А – множество людей на Земле. Отношение D -» быть другом». Это отношение симметрично, т. к. если человек х друг человека у , то и у друг х . Отношение D – «быть сыном» не является симметричным, т. к. если х сын у, то у не обязан быть сыном х (более сильно, у не сын х ).

3. Антисимметричность : хDу и yDx => x = у, т. е. хDу и
х у => у х. Тогда отношение «быть сыном» на множестве А всех людей на Земле является антисимметричным, т. к. « х сын у » влечет за собой –“ у не сын х ”.

4. Асимметричность: не выполняется ни для каких х и у А . Примером асимметричного отношения является отношение “больше” на R , т. к. ни про какую пару вещественных чисел ( х; у ) нельзя сказать, что одновременн о х > у и у > х.

5. Транзитивность: хDу, уDz = > хDz.

Другими словами, если х находится в отношении D с у , а у находится в отношении D с z , то х находится в отношении D с z . Например, отношение «быть другом» не является транзитивным, т. к. из условия х друг у , а у друг z , еще не следует, что х друг z . Если бинарное отношение D на множестве А рефлексивно, симметрично, транзитивно, то оно называется эквивалентным или эквивалентностью. Например, путь А – множество прямых на плоскости. Ведем отношение «параллельность прямых» следующим образом: прямая а тогда и только тогда параллельна прямой b , когда прямые а и b не имеют общих точек или совпадают. Тогда отношение «параллельность прямых»:

1) рефлексивно, т. к. любая прямая плоскости параллельна сама себе;

2) симметрично, т. к. если а || b , то b || а ;

3) транзитивно, т. к. если а || b и b||с , то а || с .

При решении конкретных задач часто не удобно работать с элементами множества. Например, мы имеем множество спортсменов в данном клубе. Работать персонально с каждым (оформлять поездки, расписание занятий и т.п.) неудобно. Поэтому часто более удобно работать с группами (классами) элементов данного множества. Явно удобнее работать со спортсменами, распределенными, например, по группам, а в каждой группе распределять спортсменов на подгруппы по мастерству и т. п. Чтобы обобщить такого сорта задачи в теории множеств вводится понятие разбиения множества.

Пусть А – непустое множество. И пусть – набор подмножеств множества А , обладающий следующими свойствами:

Тогда набор множеств , называется разбиением множества А . Например, дано множество А – студентов первого курса дневного обучения географического факультета. Мы имеем несколько разбиений этого множества. Например, по специальностям: «Геоэкология», «География», «Картография». Можно указать и другое разбиение: по изучаемым иностранным языкам и т. д.

Если на множестве А задано бинарное отношение D , являющееся эквивалентностью, т. е. D рефлексивно, симметрично, транзитивно, то можно создать разбиение множества А по отношению эквивалентности D :

1 шаг. Возьмем из А какой-нибудь элемент, например а . Соберем в один класс СI а все элементы из множества А , находящиеся в отношении D с элементом а : СI а = < х | х А, хDа >. Если СI а = А , то разбиение состоит из одного класса. Если СI а А, то существует b А: b СI а , т. е. b а .

2 шаг. Соберем в один класс СI b все элементы множества А , находящиеся в отношении D с элементом b : СI b = < х | х А, хDb >.

Если СI а СI b = А , то разбиение состоит из двух классов (СI а и СI b ). Если СI а СI b А , то существует элемент с А, с СI а СI b , т.е . с СI а и с СI b .

3 шаг. Собираем СI с = < х | х А, хDс > и т. д.

Процесс может быть конечным, может быть бесконечным – в зависимости от типа множества А и типа отношения.

За счет рефлективности, симметричности и транзитивности отношения D можно сказать, что:

1) каждый класс не пуст;

2) пересечение двух любых разных классов пусто;

3) объединение полученных классов дает множество А .

Значит, зная некую эквивалентность на данном множестве, всегда можно иметь разбиение этого множества по данной эквивалентности. Верно и обратное. Если на множестве А задано некоторое разбиение, то среди всех возможных эквивалентностей на множестве А можно найти такую, которая задает именно данное разбиение. Покажем, каким образом это можно сделать. Пусть на множестве А задано какое-нибудь разбиение. Зададим на это множестве А отношение D: xD y у “Элемент х находится в том же классе разбиения, что и элемент у ”. Это отношение обладает свойствами:

1) рефлексивность: т. к. любой элемент х находится в одном классе разбиения с самим собой;

2) симметричность : xDy => yDx , т. к. если элемент х находится в одном классе с элементом у , т о у находится в одном классе с элементом х ;

3) транзитивность: xDy, yDz => xDz , т. к. если х лежит в одном классе с элементом у , который лежит в одном классе с элементом z , то х лежит в том же классе, что и элемент z (по определению разбиения множества А ).

Итак, отношение D : ”находится в одном и том же классе разбиения” рефлексивно, симметрично, транзитивно. Следовательно, D – отношение эквивалентности на множестве А . Другими словами, разбиение множества А и эквивалентности на этом множестве задают друг друга.

Кроме отношения эквивалентности, большую роль играют отношения, называемые отношениями порядка. Бинарное отношение D на множестве А называется отношением порядка, если оно транзитивно и антисимметрично. Множество А, на котором задано отношение порядка, называется упорядоченным множеством.

Не следует думать, что все отношения подразделяются только на отношения эквивалентности и отношения порядка. Существует огромное число отношений, не являющихся ни отношением эквивалентности, ни отношением порядка, но играющих важную роль в решении различных задач.

Содержание

Свойства отношений на множестве
Параллельные прямые, признаки и условия параллельности прямых
Параллельные прямые: основные сведения
Параллельность прямых: признаки и условия параллельности
Параллельность прямых в прямоугольной системе координат
🔥 Видео

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Свойства отношений на множестве

Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой: хRх. Если отношение рефлексивно, то в каждой вершине графа имеется петля. И обратно, граф, каждая вершина которого содержит петлю, представляет собой граф рефлексивного отношения.

Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др.

Существуют отношения, не обладающие свойством рефлексивности, например, отношение перпендикулярности отрезков: ab, ba (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе). Поэтому на графе данного отношения нет ни одной петли.

Не обладает свойством рефлексивности и отношение «длиннее» для отрезков, «больше на 2» для натуральных чисел и др.

Отношение R на множестве Х называется антирефлексивным, если для любого элемента из множества Х всегда ложно хRх: .

Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны сами себе, а точки, не лежащие на прямой l, себе не симметричны.

Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении с элементом y, следует, что и элемент y находится в отношении R с элементом х: xRyyRx .

Граф симметричного отношения обладает следующей особенностью: вместе с каждой стрелкой, идущей от х к y, граф содержит стрелку, идущую от y к х (рис. 35).

Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др.

Существуют отношения, которые не обладают свойством симметричности.

Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Граф этого отношения обладает особенностью: стрелка, соединяющая вершины, направлена только в одну сторону.

Отношение R называют антисимметричным, если для любых элементов х и y из истинности xRy следует ложность yRx: : xRyyRx.

Кроме отношения «длиннее» на множестве отрезков существуют и другие антисимметричные отношения. Например, отношение «больше» для чисел (если х больше у, то у не может быть больше х), отношение «больше на» и др.

Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности.

Отношение R на множестве Х называют транзитивным, если из того, что элемент х находится в отношении R с элементом y, а элемент y находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z: xRy и yRzxRz.

Граф транзитивного отношения с каждой парой стрелок, идущих от х к y и от y к z, содержит стрелку, идущую от х к z.

Свойством транзитивности обладает и отношение «длиннее» на множестве отрезков: если отрезок а длиннее отрезка b, отрезок b длиннее отрезка с, то отрезок а длиннее отрезка с. Отношение «равенства» на множестве отрезков также обладает свойством транзитивности: (а=b, b=с)(а=с).

Существуют отношения, которые не обладают свойством транзитивности. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку b, а отрезок b перпендикулярен отрезку с, то отрезки а и с не перпендикулярны!

Существует еще одно свойство отношений, которое называется свойством связанности, а отношение, обладающее им, называют связанным.

Отношение R на множестве Х называется связанным, если для любых элементов х и y из данного множества выполняется условие: если х и y различны, то либо х находится в отношении R с элементом y, либо элемент y находится в отношении R с элементом х. С помощью символов это определение можно записать так: xy xRy или yRx.

Например, свойством связанности обладает отношение «больше» для натуральных чисел: для любых различных чисел х и y можно утверждать, либо x>y, либо y>x.

На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.

Существуют отношения, которые не обладают свойством связанности. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и y, что ни число х не является делителем числа y, ни число y не является делителем числа х (числа 17 и 11, 3 и 10 и т.д.).

Рассмотрим несколько примеров. На множестве Х= задано отношение «число х кратно числу y». Построим граф данного отношения и сформулируем его свойства.

Про отношение равенства дробей говорят, оно является отношением эквивалентности.

Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойством рефлексивности, симметричности и транзитивности.

Примерами отношений эквивалентности могут служить: отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).

В рассмотренном выше отношении «равенства дробей», множество Х разбилось на три подмножества: <; ; >, <; >, <>. Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеем разбиение множества на классы.

Итак, если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества – классы эквивалентности.

Так, мы установили, что отношению равенства на множестве
Х= <;; ; ; ; > соответствует разбиение этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.

Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики. Почему?

Во-первых, эквивалентный – это значит равносильный, взаимозаменяемый. Поэтому элементы одного класса эквивалентности взаимозаменяемы. Так, дроби, оказавшиеся в одном классе эквивалентности <; ; >, неразличимы с точки зрения отношения равенства, и дробь может быть заменена другой, например . И эта замена не изменит результата вычислений.

Во-вторых, поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом класса. Так, любой класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, порождает разбиение этого множества на классы треугольников, четырехугольников, пятиугольников и т.д. свойства, присущие некоторому классу, рассматриваются на одном его представителе.

В-третьих, разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий. Например, понятие «пучок прямых» можно определить как то общее, что имеют параллельные прямые между собой.

Другим важным видом отношений являются отношения порядка. Рассмотрим задачу. На множестве Х=<3, 4, 5, 6, 7, 8, 9, 10> задано отношение «иметь один и тот же остаток при делении на 3». Это отношение порождает разбиение множества Х на классы: в один попадут все числа, при делении которых на 3 получается в остатке 0 (это числа 3, 6, 9). Во второй – числа, при делении которых на 3 в остатке получается 1 (это числа 4, 7, 10). В третий попадут все числа, при делении которых на 3 в остатке получается 2 (это числа 5, 8). Действительно, полученные множества не пересекаются и их объединение совпадает с множеством Х. Следовательно, отношение «иметь один и тот же остаток при делении на 3», заданное на множестве Х, является отношением эквивалентности.

Возьмем еще пример: множество учащихся класса можно упорядочить по росту или возрасту. Заметим, что это отношение обладает свойствами антисимметричности и транзитивности. Или всем известен порядок следования букв в алфавите. Его обеспечивает отношение «следует».

Отношение R на множестве Х называется отношением строгого порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности. Например, отношение «х Просмотров 153 479 Комментариев 0

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

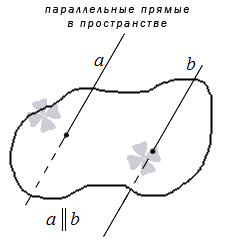
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а .

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

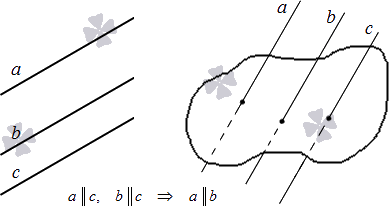
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

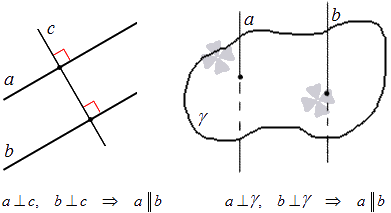
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = ( a x , a y ) и b → = ( b x , b y ) являются направляющими векторами прямых a и b ;

и n b → = ( n b x , n b y ) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.

Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты ( А 1 , В 1 ) и ( А 2 , В 2 ) соответственно. Условие параллельности запишем так:

A 1 = t · A 2 B 1 = t · B 2

Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) соответственно, а условие параллельности запишем так:

k 1 = t · k 2 — 1 = t · ( — 1 ) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .

Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:

a x = t · b x a y = t · b y

Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0

Мы видим, что n a → = ( 2 , — 3 ) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .

Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:

2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?

Решение

Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:

x 1 = y — 4 2 ⇔ 1 · ( y — 4 ) = 2 x ⇔ y = 2 x + 4

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, ( 0 , 1 ) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Нормальный вектор прямой y = 2 x + 1 это вектор n a → = ( 2 , — 1 ) , а направляющий вектором второй заданной прямой является b → = ( 1 , 2 ) . Скалярное произведение этих векторов равно нулю:

n a → , b → = 2 · 1 + ( — 1 ) · 2 = 0

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.

Решение

Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: ( 1 , 0 , — 3 ) и ( 2 , 0 , — 6 ) .

1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.