Отношение хорды и дуги окружности

Окружность есть такая плоская кривая, у которой все точки находятся на равном расстоянии от одной точки, лежащей внутри ее и называемой центром.

Круг. Кругом называется часть плоскости, ограниченная окружностью.

Радиус. Радиусом называется отрезок, соединяющий центр с какой-нибудь точкой окружности. Радиус есть расстояние точки окружности от центра.

Из самого определения окружности следует, что все ее радиусы равны.

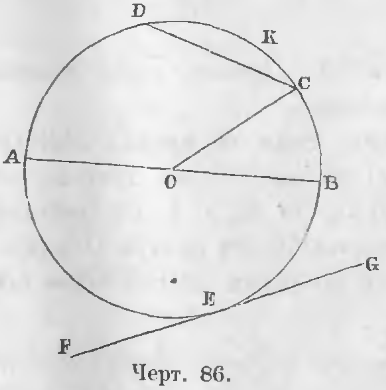
На чертеже 86 кривая линия BCDAEB есть окружность, O ее центр, отрезки OA, OB, OC — радиусы. Эти отрезки равны

Диаметр. Отрезок, проходящий через центр от одной точки окружности до другой, называется диаметром.

Всякий диаметр состоит из двух радиусов, а так как все радиусы равны, то следовательно и все диаметры равны.

Дуга есть часть окружности.

Слово дуга иногда обозначают знаком ◡, так что дугу BC изображают письменно: ◡BC.

Хорда. Отрезок, соединяющий две какие-нибудь точки окружности, называется хордой. Хорда есть прямая, стягивающая две точки дуги.

На чертеже 86 линия AB есть диаметр, часть окружности BC есть дуга, прямая CD есть хорда.

Сегмент есть часть плоскости, содержащийся между дугой и хордой.

Сектор есть часть плоскости, содержащийся между двумя радиусами и дугой круга.

На чертеже 86 площадь COB есть сектор, а CKD сегмент.

Касательная есть прямая, имеющая с окружностью только одну общую точку, которая называется точкой касания.

Углом при центре называется угол, имеющий вершину в центре. На чертеже 86 прямая FG есть касательная, а E точка касания.

Теорема 55. Прямая может пересечь окружность только в двух точках.

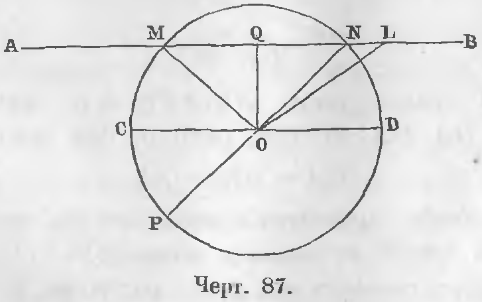
Доказательство. Если бы прямая AB кроме двух точек M и N (черт. 87) имела бы еще третью точку пересечения L, то три точки окружности M, N, L, по свойству окружности, были бы на равном расстоянии от центра O, следовательно, три отрезка MO, NO, LO были бы равны: MO = NO = LO.

Если же NO = LO, то вышло бы, что равные наклонные находятся на неравных расстояниях от перпендикуляра OQ, что противоречит свойству косвенных, следовательно, третьей точки пересечения быть не может (ЧТД).

Теорема 56. Диаметр делит окружность и круг на две равные части.

Доказательство. Перегнем верхнюю часть круга около диаметра CD (черт. 87) до совпадения ее с нижней частью, тогда все точки верхней совпадут с точками нижней части окружности, ибо в противном случае не все точки окружности находились бы на равном расстоянии от центра.

Зависимость между углами, дугами и хордами

Теорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги.

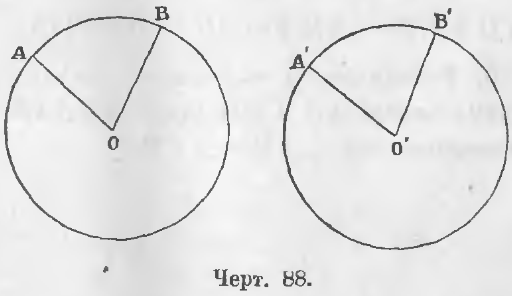
Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны:

Требуется доказать, что ◡AB = ◡A’B’.

Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами.

Теорема 58 (обратная 57). Равным дугам соответствуют равные углы.

Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88).

Требуется доказать, что ∠AOB = ∠A’O’B’.

Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно,

Теорема 59. Диаметр больше всякой хорды.

Даны диаметр CD и хорда MN (черт. 87).

Требуется доказать, что CD > MN.

Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN

MON > MN или MO + ON > MN

Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства:

CO + OD > MN или CD > MN (ЧТД).

Теорема 60. Равные хорды стягивают равные дуги.

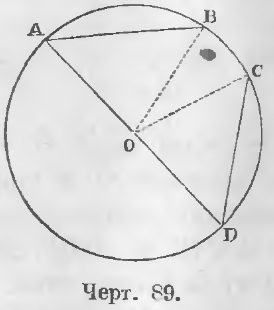
Даны равные хорды AB и CD (черт. 89) (AB = CD).

Требуется доказать, что ◡AB = ◡CD.

Доказательство. Соединив точки A, B, C, D с центром, имеем

OA = OC и OB = OD как радиусы, AB = CD по условию.

Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД).

Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами.

Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD).

Требуется доказать, что AB = CD.

Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД).

Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда.

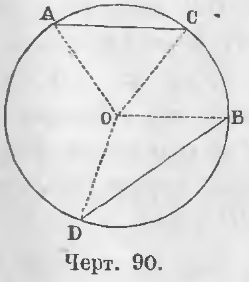
Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC).

Требуется доказать, что BD > AC.

Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД).

Теорема 63 (обратная 62). Против большей хорды лежит большая дуга.

Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC).

Требуется доказать, что ◡BD > ◡AC.

Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД).

Взаимное отношение хорд и их расстояний от центров

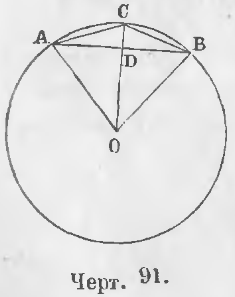
Теорема 64. Радиус, перпендикулярный к хорде, делит как хорду так и дугу пополам.

Радиус OC перпендикулярен к хорде AB (черт. 91).

Требуется доказать, что AD = BD и ◡AC = ◡CB.

Доказательство. Соединим точки A и B с центром O. Равные наклонны OA и OB находятся на равных расстояниях от перпендикуляра OC, следовательно, AD = DB.

Если же перпендикуляр CD восставлен из середины отрезка AB, то его точка C находится на равном расстоянии от концов перпендикуляра, поэтому хорды AC и CB равны, а следовательно,

т. е. дуга AB делится перпендикуляром OC пополам (ЧТД).

Следствие. Перпендикуляр, восставленный из середины хорды, проходит через центр.

Доказательство. Так как центр находится на равном расстоянии от концов хорды, то он находится на перпендикуляре, восставленном из середины хорды.

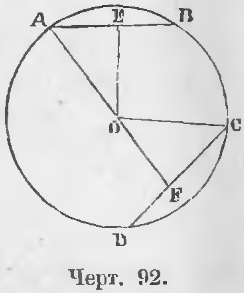
Теорема 65. Равные хорды находятся на равном расстоянии от центра.

Дано. Хорды AB и CD равны: AB = CD (черт. 92).

Требуется доказать, что их расстояния от центра равны, т. е.

Доказательство. Соединив точки A и C с центром O, имеем два равных прямоугольных треугольника AEO и COF, ибо OA = OC как радиусы, AE = CF как половины равных хорд (теорема 64). Следовательно,

Теорема 66 (обратная 65). На равных расстояниях от центра находятся равные хорды.

Дано. Расстояния хорд AB и CD от центра равны, т. е.

Требуется доказать, что AB = CD.

Доказательство. Два прямоугольных треугольника AEO и COF равны, ибо имеют по равной гипотенузе и равному катету. Действительно, OE = OF по условию, OA = OC как радиусы, следовательно, AE = CF или ½AB = ½CD, откуда

Теорема 67. Большая хорда к центру ближе меньшей.

Дано. Хорда AB больше хорды AC (черт. 93), т. е. AB > AC.

Требуется доказать, что OD ⊥ AO.

Требуется доказать, что AF касательная к окружности.

Доказательство. Всякая другая точка B перпендикуляра AB находится на расстоянии BO большем AO, ибо наклонная больше перпендикуляра, следовательно точка B находится вне окружности. Таким образом прямая AB имеет с окружностью только одну общую точку A, следовательно, она будет касательной (ЧТД).

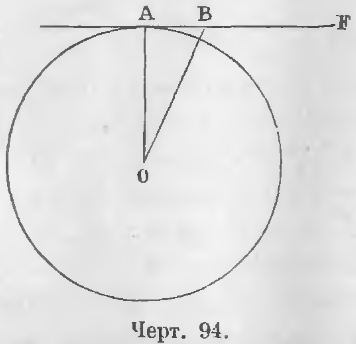
Теорема 69 (обратная 68). Касательная к окружности, проведенная в конец радиуса, перпендикулярна к радиусу.

Дано. Прямая AF касается окружности в точке A (черт. 94).

Требуется доказать, что AF ⊥ OA.

Доказательство. Прямая AB как касательная имеет с окружностью только одну общую точку A. Всякая другая точка B лежит вне окружности, следовательно, всякий отрезок OB больше OA. Таким образом, отрезок OA есть кратчайшее расстояние точки O от AB, следовательно, OA ⊥ AB (ЧТД).

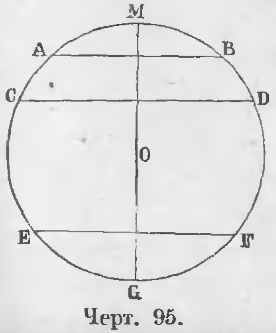
Теорема 70. Между параллельными хордами находятся равные дуги.

Дано. Хорды AB и CD параллельны: AB || CD (черт. 95).

Требуется доказать, что ◡AC = ◡BD.

Доказательство. a) Из центра окружности O опустим перпендикуляр OM на хорду AB, тогла отрезок OM перпендикулярен и к хорде CD.

Вычитая второе равенство из первого, получим:

◡CM — ◡AM = ◡MD — ◡MB или
◡AC = ◡BD.

b) Если параллельные хорды AB и EF (черт. 95) лежат по обе стороны центра, то, продолжив прямую OM до пересечения с окружностью в точке G, имеем:

Так как полуокружности MAG и MBG равны

MAG = MBG, то следовательно,
MAG — ◡MA — ◡GE = MBG — ◡MB — ◡GF
или ◡AE = ◡BF (ЧТД).

Относительное положение двух окружностей

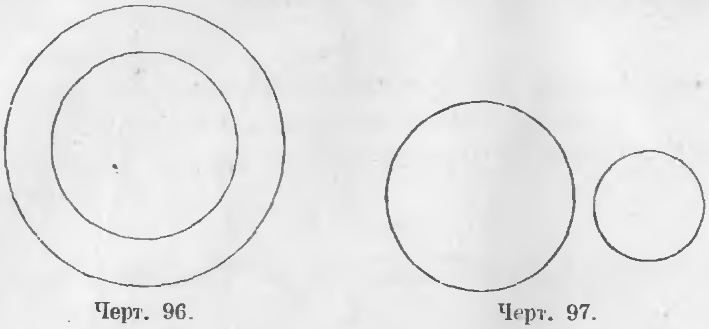
Концентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают.

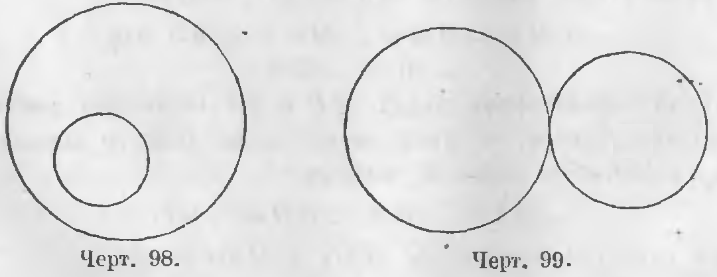
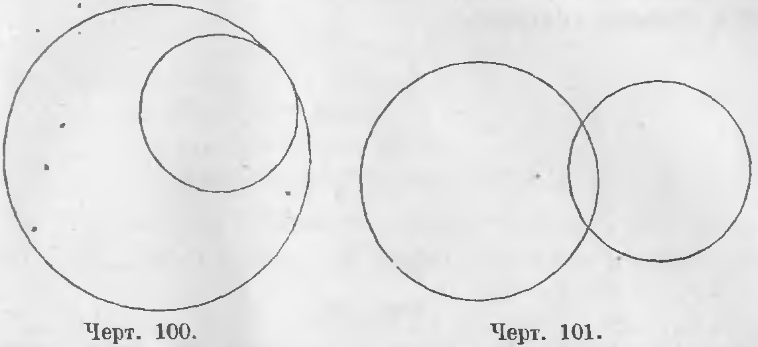
На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические.

Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга.

На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние.

Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку.

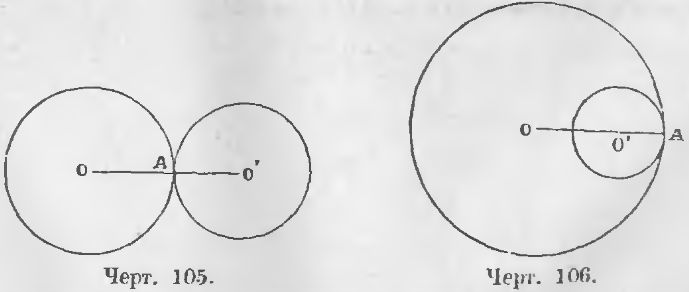
Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения.

Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101).

Линия центров есть отрезок, соединяющий центры двух кругов.

Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут.

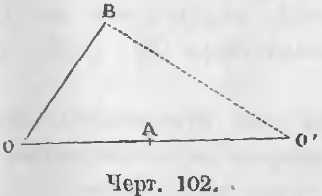
Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102).

Требуется доказать, что другой общей точки у них нет.

Доказательство. Положим, существует другая общая точка B, следовательно,

OB = OA и O’B = O’A.

Складывая эти равенства, мы имели бы

OB + O’B = OA + O’A или
OB + O’B = OO’

равенство несообразное, ибо ломаная не может равняться прямой.

Итак, другой общей точки быть не может (ЧТД).

Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров.

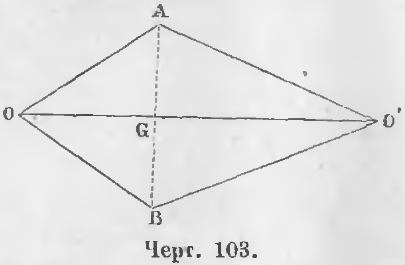
Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры.

Требуется доказать, что существует и другая общая точка по другую сторону центров.

Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG.

Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД).

Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения.

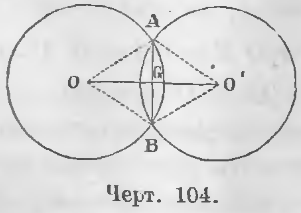
Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей.

Требуется доказать, что AG = BG и AB ⊥ OO’.

Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая.

OA = OB как радиусы окружности O.

O’A = O’B как радиусы окружности O’.

Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров).

Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД).

Расстояние между центрами окружностей

1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов.

Действительно, с одной стороны (черт. 104)

2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее.

Из чертежа 105 видно, что

а из чертежа 106

3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов.

Из чертежа 107 видно, что

4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов.

Действительно, из чертежа 108 видно, что

Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.

Положим, мы нашли, что имеет место равенство

Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,

Разделив равенства (b) на (a), находим

равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.

AOB/AOF ∆ ObC
∆ ObD = ∆ OcD
∆ OcA = ∆ OdA
∆ OdB = ∆ OaB

ибо они, будучи прямоугольными, имеют по равной гипотенузе OC, OD, OA, OB и равным катетам, следовательно,

aC = bC
aB = dB
cA = dA
cD = bD

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

📽️ Видео