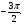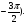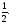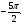Отметьте на тригонометрической окружности точки соответствующие углам

Алгебра | 10 — 11 классы

Выделите точки на тригонометрической окружности так , чтобы для соответствующих им углов выполнялось условие |cosα|≤√2 / 2.

Смотрим прикреплённый файл.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Отметьте точки единичной окружности , соответствующие углам АЛЬФА, для каждого из которых выполняется равенство, и задайте эти углы формулой : а) tg альфа = 1 б) ctg альфа = 0 в) ctg альфа = — 1 г) tg?

Отметьте точки единичной окружности , соответствующие углам АЛЬФА, для каждого из которых выполняется равенство, и задайте эти углы формулой : а) tg альфа = 1 б) ctg альфа = 0 в) ctg альфа = — 1 г) tg альфа = — корень из 3 д) ctg альфа = корень из 3

добавьте во вложение.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

На числовой окружности укажите все точки, координаты которых удовлетворяют данным условиям, и составьте формулы для всех чисел, которым соответствуют эти точки :y = — 1 / 2 , x &gt ; 0?

На числовой окружности укажите все точки, координаты которых удовлетворяют данным условиям, и составьте формулы для всех чисел, которым соответствуют эти точки :

Видео:Как искать точки на тригонометрической окружности.Скачать

Как найти на числовой окружности точки?

Как найти на числовой окружности точки.

Которые соответствуют числам 4, 5 и — 3?

Какой четверти числовой окружности принадлежат точки, соответствующих числам 8, 4 , 3, и — 8?

Видео:Отбор корней по окружностиСкачать

Помогите решить тригонометрическое выражение?

Помогите решить тригонометрическое выражение.

Найдите 18cos2α, если cosα = 0.

Видео:Изобразить на единичной окружности точку.Скачать

Найдите все числа, которым соответствуют отмеченные на числовой окружности точки?

Найдите все числа, которым соответствуют отмеченные на числовой окружности точки.

Видео:Тригонометрическая окружность. Как выучить?Скачать

На числовой окружности укажите все точки, координаты которых удовлетворяют данным условиям, и составьте формулы для всех чисел, которым соответствуют эти точки :y = — 1 / 2 , x &gt ; 0?

На числовой окружности укажите все точки, координаты которых удовлетворяют данным условиям, и составьте формулы для всех чисел, которым соответствуют эти точки :

Видео:5. Как найти точки на тригонометрической окружности. Отрицательные углы в градусах и радианах.Скачать

Найдите косинус угла a, изображенного на тригонометрической окружности?

Найдите косинус угла a, изображенного на тригонометрической окружности.

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Отметьте точки единичной окружности, соответствующие углам альфа, для каждого из которых выполняется равенство : tg alfa = 4 ?

Отметьте точки единичной окружности, соответствующие углам альфа, для каждого из которых выполняется равенство : tg alfa = 4 ;

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Вычислите с помощью тригонометрической окружности ?

Вычислите с помощью тригонометрической окружности :

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Указать число соответствующее выделенной точке окружности СРОЧНО прошу?

Указать число соответствующее выделенной точке окружности СРОЧНО прошу.

На этой странице сайта, в категории Алгебра размещен ответ на вопрос Выделите точки на тригонометрической окружности так , чтобы для соответствующих им углов выполнялось условие |cosα|≤√2 / 2?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Если я не ошибаюсь, то область значений является интервал от 0 до 5. То есть значение y на данном графике.

Производная функции у = 3sinx, это у’ = 3соsx, так как 3 выходит из знака производной(потому что она постоянная), а (sinx)’ = cosx.

3 — постоянный множитель, его можно вынести за знак производной : не забываем про константу : ответ : y’ = 3cosx.

2х² + 3х — 5 = 0 D = 3² — 4 • ( — 5) • 2 = 49 х1 = — 3 — 7 / 4 = — 2, 5 х2 = — 3 + 7 / 4 = 1 Ответ : — 2, 5 ; 1.

Под вторым корнем отрицательное число — условие верно? Если второй корень квадратный то ответ : 6. 0049 — 0. 13729i.

Геометрический смысл определённого интеграла — это площадь криволинейной трапеции, которая ограничена линиями, , и Если известны a и b, а также функция непрерывна на отрезке, то определённый интеграл этой функции находится по формуле Ньютона — Лейбн..

1 / x² — 1 / x — 6 = 0 Сводим к общему знаменателю и опускаем их. 1 — x — 6x² = 0 Упорядочим множители : — 6x² — x + 1 = 0 | : ( — 1) 6x² + x — 1 = 0 Методом переброски решаем квадратное уравнение : Для этого старший коэффициент делим само на себя и..

16x² + 25 = 0 x² = — 25 / 16 Действительных корней нет. X² = i² * 25 / 16 x = ±5i / 4.

Видео:Как определять угол на тригонометрической окружностиСкачать

Контрольный срез «Тригонометрический круг»

Контрольный срез по теме «Тригонометрический круг» предназначен для проверки знаний учащихся 10 класса. В процессе выполнения заданий учащимся необходимо показать свои умения определять по кругу табличные значения тригонометрических функций, отмечать на тригонометрическом круге точки, соответствующие данным углам, а так же решать простейшие тригонометрические неравенства.

Просмотр содержимого документа
«Контрольный срез «Тригонометрический круг»»

Контрольный срез по материалу курса алгебры и начал анализа 10 класса

Отметьте на тригонометрическом круге точки, соответствующие углам:

а) б) в) г)

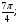
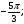
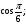
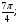
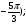
а) б) tg в) sin( г) cos(

Укажите множество точек окружности, для которых:

а) cost = б) sint =

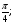
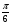
а) 2cos60 o – tg б) ctg45 o -2sin.

Укажите дугу окружности, множество точек которой удовлетворяет условию:

а) cost б) sint

Найдите наименьшее и наибольшее значение выражения 0,5cost +2.

Контрольный срез по материалу курса алгебры и начал анализа 10 класса

Отметьте на тригонометрическом круге точки, соответствующие углам:

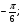
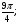
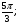
а) б) в) г)

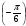
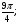
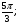
а) cos; б) tg в) sin г) cos(

Укажите множество точек окружности, для которых:

а) cost = 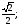б) sin t =

Укажите дугу окружности, множество точек которой удовлетворяет условию:

а) cos t б) sin t

Найдите наименьшее и наибольшее значение выражения 3sin t – 1 .

Оценка «3» , если набрано 10 – 12 баллов; Оценка «4» , если набрано 13 – 15 баллов;

Оценка «5» , если набрано 16 — 20 баллов.

Видео:ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэ #окружностьСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Тригонометрическая окружность для непонимающихСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

🌟 Видео

Радианная мера угла. 9 класс.Скачать

Точки на числовой окружностиСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Выборка с помощью окружностиСкачать

ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬСкачать