Основная окружность зубчатого колеса внутреннего зацепления

Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. При проектировании зубчатого колеса вначале нужно определить его число зубьев z , а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса r y разделить на z частей, каждая из которых называется окружным шагом p y .

где m y = p y / p = d y / z — модуль зацепления по окружности произвольного радиуса.

Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p . В зависимости от окружности по которой определен модуль различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) — число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого модуль можно определить как число милиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба). Угловой шаг t — центральный угол соответствующий дуге p — окружному шагу по делительной окружности.

Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины — строчными буквами латинского алфавита, угловые — греческими буками; установлены индексы для величин :

по окружностям: делительной — без индекса, вершин — a , впадин — f , основная — b , начальная — w , нижних точек активных профилей колес — p , граничных точек — l ;

по сечениям: нормальное сечение — n , торцевое сечение — t , осевое сечение — x ;

относящихся к зуборезному инструменту — 0 .

Для параметров зубчатого колеса справедливы следующие соотношения

— диаметр окружности произвольного радиуса,

— диаметр делительной окружности,

— шаг по окружности произвольного радиуса,

— шаг по делительной окружности,

где a — угол профиля на делительной окружности,

a y — угол профиля на окружности произвольного радиуса.

Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом — вектором, проведенным в данную точку из центра колеса.

Шаг колеса делится на толщину зуба s y и ширину впадины e y . Толщина зуба s y — расстояние по дуге окружности r y между разноименными точками профилей зуба. Ширина впадины e y — расстояние по дуге окружности r y между разноименными точками профилей соседних зубьев.

На основной окружности a b => 0 и cos a b => 1 , тогда

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:

нулевые s = e = p * m / 2 , D = 0;

положительные s > e , => D > 0;

отрицательные s D D — коэффициент изменения толщины зуба (отношение приращения толщины зуба к модулю). Тогда толщину зуба по делительной окружности можно записать

Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.

Толщина зуба колеса по окружности произвольного радиуса .

Толщина зуба по дуге делительной окружности

Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2

Подставляя в формулу угловой толщины эти зависимости, получим

Методы изготовления эвольвентных зубчатых колес .

Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:

метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности ( конгруентны ей, т. е. заполняют эту поверхность как отливка заполняет форму );

метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения — резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению , т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения).

Из вариантов изготовления по способу копирования можно отметить:

Нарезание зубчатого колеса профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой соответствует конфигурации впадин). При этом методе резание производится в следующем прядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются пока не будут прорезаны все впадины. Производительность данного способа низкая, точность и качество поверхности невысокие.

Отливка зубчатого колеса в форму. При этом внутренняя поверхность литейной формы конгруентна наружной поверхности зубчатого колеса. Производительность и точность метода высокая, однако при этом нельзя получить высокой прочности и твердости зубьев.

Из вариантов изготовления по способу огибания наибольшее распространение имеют:

Обработка на зубофрезерных или зубодолбежных станках червячными фрезами или долбяками. Производительность достаточно высокая, точность изготовления и чистота поверхностей средняя. Можно обрабатывать колеса из материалов с невысокой твердостью поверхности.

Накатка зубьев с помощью специального профилированного инструмента. Обеспечивает высокую производительность и хорошую чистоту поверхности. Применяется для пластичных материалов, обычно на этапах черновой обработки. Недостаток метода образование наклепанного поверхностного слоя, который после окончания обработки изменяет свои размеры.

Обработка на зубошлифовальных станках дисковыми кругами. Применяемся как окончательная операция после зубонарезания (или накатки зубьев) и термической обработки. Обеспечивает высокую точность и чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью.

Понятие о исходном, исходном производящем и производящем контурах .

Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:

для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения — исходный контур;

для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения — исходный производящий контур.

По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:

угол главного профиля a = 20 ° ;

коэффициент высоты зуба h * a = 1 ;

коэффициент высоты ножки h * f = 1.25 ;

коэффициент граничной высоты h * l = 2 ;

коэффициент радиуса кривизны переходной кривой r * f =с * /(1-sin a )= 0.38 ;

коэффициент радиального зазора в паре исходных контуров с * = 0.25.

Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.

Исходный и исходный производящий контуры образуют между собой конруентную пару (рис. 12.3), т.е. один заполняет другой как отливка заполняет заготовку (с радиальным зазором с * Ч m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий — в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура — проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки.

Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.

Линия станочного зацепления — геометрическое место точек контакта эвольвентной части профиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.

Смещение исходного производящего контура x*m — кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.

Уравнительное смещение D y*m — условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).

Окружность граничных точек r l — окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.

Основные размеры зубчатого колеса .

Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).

Радиус окружности вершин

Радиус окружности впадин

Толщина зуба по делительной окружности.

Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать

Виды зубчатых колес (Классификация по величине смещения) .

В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.

Подрезание и заострение зубчатого колеса .

Если при нарезании зубчатого колеса увеличивать смещение, то основная и делительная окружность не изменяют своего размера, а окружности вершин и впадин увеличиваются. При этом участок эвольвенты, который используется для профиля зуба, увеличивает свой радиус кривизны и профильный угол. Толщина зуба по делительной окружности увеличивается , а по окружности вершин уменьшается.

На рис. 12.7 изображены два эвольвентных зуба для которых

Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого

При этом удобнее пользоваться относительными величинами [s a /m ]. Обычно принимают следующие допустимые значения

улучшение, нормализация [s a /m ] = 0.2;

цианирование, азотирование [s a /m ] = 0.25. 0.3;

цементация [s a /m ] = 0.35. 0.4.

Подрезание эвольвентных зубьев в станочном зацеплении

В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком B 1 . где точка B l определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка B l располагается ниже (см. рис.12.8) точки N , то возникает подрезание зуба. Условие при котором нет подрезания можно записать так

Видео:Построение эвольвентного зацепленияСкачать

Детали машин

Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Геометрические параметры эвольвентного зацепления

Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.

В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:

• w – начальной;
• b – основной;
• a – вершин зубьев;
• f – впадин зубьев.

Параметрам, относящимся к делительной окружности, индекс не присваивается.

При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» — колесу.

Начальные окружности

Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О₁ и О₂ до полюса П ) при неизменном межосевом расстоянии О₁О₂ тоже остается неизменным.
При изменении межосевого расстояния a_w меняются и диаметры d_w начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.

Межосевое расстояние определяется по формуле:

Делительная окружность

Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.

Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:

Исключение составляют передачи с угловой модификацией.

Окружной шаг зубьев

Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.

Основной шаг

Этот параметр, обозначаемый p_b , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу p_b .
Из треугольника О₂ВП (см. рис. 1) диаметр основной окружности d_b2 = 2 r_b2 = d₂ cos α_w , откуда основной шаг может быть определен по формуле:

Окружная толщина зуба и окружная ширина впадины

Окружная толщина зуба s_t и окружная ширина впадины e_t по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер s_t назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда s_t + e_t = p .

Окружной модуль зубьев

Из определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно,

Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах:

d = mz или m = d/z .

Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).

При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.

Высота головки и ножки зуба

Делительная окружность делит зуб по высоте на головку h_a и ножку h_f . Для создания радиального зазора с (см . рис. 1) необходимо

Для передачи без смещения h_a = m .

Длина активной линии зацепления

При вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S» пересечения линии зацепления с окружностью вершин шестерни.
Отрезок S’S» линии зацепления называют длиной активной линии зацепления и обозначают g_α . Длину g_α легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S» и замеряют g_α .

Коэффициент торцового перекрытия

Коэффициентом торцового перекрытия ε_α называют отношение длины активной линии зацепления к основному шагу:

где z₁ и z₂ – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.

Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.

За период работ пары зубьев точка их зацепления проходит путь, равный по длине g_α (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу p_b . При g_α > p_b необходимое перекрытие зубьев обеспечивается.

По условию непрерывности зацепления должно быть ε_α > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия ε_α .

Видео:Построение эвольвенты окружностиСкачать

Зубчатое колесо

Зубчатые передачи весьма широко и продуктивно применяются в конструкциях современных машин, механизмов и устройств. Транспортные средства, энергетические установки, грузоподъемные устройства, авиационные установки, сельскохозяйственные машины, точные приборы — во всех них найдутся те или иные варианты зубчатого колеса. В технике зубчатая передача используется с целью распространения вращательного движения между осями валов, которые могут быть расположены параллельно, скрещиваться или пересекаться. Также, при помощи подобной передачи легко преобразовать вращательное движение, например, в поступательное, или реализовать эффективное преобразование крутящего момента и оборотов валов. Благодаря последнему свойству их используют в редукторах или мультипликаторах различных типов, а также коробках передач.

Основными преимуществами подобного способа передачи мощностей являются высокий КПД; компактный конструктив; плавная работа; точность; долговечность; надежность; возможность осуществления передачи силы с использованием любого угла, передаточного числа (до нескольких тысяч) и большого диапазона скоростей (до 150 м/с). Эти качества и обусловили распространение использования зубчатых передач в технике. К негативным моментам можно отнести технологическую сложность производства; требовательность к точности обработки, материалам и обрабатывающему оборудованию. Выбор материала для зубчатого колеса один из наиболее важных критериев надежности и долговечности в дальнейшей его работе. Жесткость конструкции, обеспечивающая передаче высокую эффективность, к сожалению, не позволяет ей держать высокие значения динамических нагрузок, часто являющихся причиной разрушения механизма. В дополнение, этим передачам характерна повышенная шумность, снижения которой можно достичь повышением качества и точности при производстве изделий.

Видео:FreeCad Шестерни эвольвентаСкачать

Что такое зубчатые колеса

В общем случае, шестерня, или зубчатое колесо — главная деталь одноименной передачи, имеет вид диска с расположенными на цилиндрической или конической поверхности зубьями. При помощи этих зубьев в процессе вращения происходит зацепление колес между собой, что позволяет реализовать перенос вращательного момента от одного вала, на котором расположено колесо, к другому. Зуб зубчатого колеса при вращении толкает зуб другого, сопряженного с ним, колеса, которое вследствие этого тоже начинает совершать вращательное движение.

Сопряженная зубчатая передача должна всегда состоять из двух типов элементов: ведущих и ведомых. При этом ведущим, по определению, называют колесо передающее (сообщающее) вращение, ведомым — то зубчатое колесо, которое имеет большой диаметр с большим количеством зубьев и приводит во вращение. В большинстве случаев используется пара зубчатых колес, одно из которых с большим числом зубьев, а другое с меньшим. Иногда элемент, несущий меньше зубьев, считается шестерней, тогда колесом считают тот, у которого зубьев больше.

Видео:ЭВОЛЬВЕНТНОЕ зубчатое зацепление шестерен. Как это работает?Скачать

Виды зубчатых колес

Все зубчатые колеса, виды которых также многочисленны, как и варианты их применения, делятся на основные типы по расположению осей валов и геометрии формы зубьев. Выделяют цилиндрические, конические, червячные, винтовые передачи. На практике, исходя из формы профиля зубьев, выделяют эвольвентные и круговые колеса, а по расположению — прямозубые и косозубые типы зубчатых колес.

Для параллельного случая расположения осей валов применяют цилиндрические передачи:

• прямозубые;
• с круговыми зубьями;
• шевронные;
• косозубые.

Конические передачи подходят для пересекающихся осей:

• с криволинейными зубьями;
• косозубые;
• с нулевым углом наклоном;
• прямозубые.

Когда оси перекрещиваются, тогда используют передачи:

Наибольшую распространенность среди машин и механизмов обрели цилиндрические зубчатые колеса. Им свойственна простота изготовления, надежность, малые габариты. Конические, червячные и винтовые виды зубчатых колес используют лишь тогда, когда компоновка машины предъявляет особые условия. Цилиндрические зубчатые передачи делятся на два существенных вида: внешнего и внутреннего зацепления. В первом варианте реализации колесо и шестерня, у которой внешнее зацепление, крутятся в направлениях, которые противоположны друг другу. Во втором — колесо внутреннего зацепления и шестерня внешнего зацепления совершают вращательное движение со направленно. Существует также реечная передача — в ней рейка с зубьями сопрягается с имеющей внешнее зацепление шестерней.

Косозубые цилиндрические колеса имеют расположенные под углом к оси зубья. Сопряженные колеса имеют одинаковый наклон зубьев, но различные его направления. У одного наклон будет правым, у другого же — левым. Наличие наклона дает возможность передавать большие, по сравнению с прямозубыми, нагрузки, способствует плавному зацеплению зубьев и снижению шума.

Шевронные колеса представляют собой пару соединенных колес с косыми зубьями, имеющими равный угол наклона, но расположенными противоположно: одно с правым, второе с левым наклоном. Это позволяет уравновесить осевые силы, тем самым снизив нагрузку на подшипник. Колеса могут иметь в середине канавку. Колеса без канавки более прочны, но сложны в изготовлении.

Винтовые цилиндрические передачи, в свою очередь, применяют для вращения валов, когда угол их перекрещивания лежит в пределах от 0 до 90 градусов. Они похожи на косозубые колеса, однако винтовая передача имеет контакт точечный, а не линейный, как косозубая. Направление наклона зубьев у всех таких сопряженных колес одинаковое. Точечный контакт зубов вызывает повышение их износа, как следствие их используют только на небольших нагрузках.

Реечные передачи составляются из зубчатых колес и реек, которые также имеют зубья. Вращаясь, цилиндрическое колесо, перемещает сопряженную рейку по перпендикулярной оси колеса прямой. Таким способом движение из вращательного превращается в поступательное. Подобная передача бывает как с косыми зубьями, так и с прямыми.

Прямозубые конические колеса обладают зубьями, пересекающими оси этих колес. Коническое расположение позволяет вращать пересекающиеся или скрещивающиеся оси. Зубья также могут быть косыми, т.е. касательными к окружности. Угол наклона зубьев у таких колес составляет не больше тридцати градусов. Снабжение конических колес зубьями с нулевым углом наклона обеспечивает первым невысокие осевые и радиальные нагрузки, дает возможность применения подшипников скольжения. Эти качества делают передачи с использованием таких колес компактными, а изготовление не затратным.

Использование криволинейных зубьев для применения в конических зубчатых колесах резко снижает шумность передач и повышает прочность. Конические передачи подобного рода всегда имеют в зацеплении как минимум два зуба, что дает им возможность выдерживать нагрузку, которая выше на 30% относительно идентичных прямозубых и колес, имеющих нулевой наклон.

Гипоидные зубчатые колеса подобны коническим, но ось ведущей шестерни у них смещена выше или ниже относительно оси колеса, которое она ведет. У таких передач шестерни имеют наклон зубьев больший, чем у колес. Нормальный шаг при этом у шестерни и зубчатого колеса будет одинаковый, а торцовый — у шестерни больше. Гипоидной передаче не присуще чистое качение или скольжение, все ее точки подвержены скольжению. Это придает ей плавность и повышенную бесшумность. Кроме того, притирка происходит быстрее и качественней. Минус — присутствие скольжения вызывает повышенный износ поверхности зубов, что требует применения для таких передач специализированных масел.

Червячные передачи цилиндрические имеют червяк, имеющий геометрию цилиндра, на котором нарезаются витки, идущие вдоль направления винтовой линии. Червячное колесо должно иметь вогнутые зубья. Линейный контакт таких зубьев обеспечивает передачу больших нагрузок. Скольжение у червячных значительно выше, чем у прочих зубчатых передач. В глобоидной передаче червяк обладает вогнутой формой. Эта особенность позволяет участвовать в процессе зацепления большему числу зубьев, что повышает величину передаваемых такой передачей нагрузок.

Спироидные передачи занимают промежуточное место между червячными и гипоидными вариантами. В отличие от червячной, у гипоидной передачи червяк имеет форму конуса и зацепляется с колесом, на котором зубья располагаются на торцевой стороне.

Видео:Производство зубчатого колеса с внутренним зацеплением методом протягиванияСкачать

Конструкция зубчатого колеса

Металлические зубчатые колеса, чертеж которых иногда довольно сложен, имеют разнообразные варианты конструкций, однако в них можно выделить три основных компоненты: венец с зубьями, ступицу и сам колесный диск. Венец зубчатого колеса является основным компонентом и на него приходится основная нагрузка. Зубья имеют различную геометрию. Наружная часть у зуба — это вершина, прилегающие к ней боковые части — головка зуба. Внутренняя часть зуба называется его ножкой. Пространство между двумя ближними ножками образует впадину колеса. Чтобы крепить шестерню или колесо на валу, в центре диска располагается ступица, имеющая сквозное отверстие, форма которого напрямую зависит от сечения вала: она может иметь форму цилиндра, квадрата или любого другого многоугольника. В случае цилиндрических валов, ступица часто имеет т.н. шпоночный паз. В целях экономии материалов и веса колеса, его диск имеет толщину, меньшую по сравнению с толщиной обода и ступицы. Часто в диске для этих целей еще выполняют различные отверстия.

Видео:Цилиндрические передачи с внутренним зацеплением...Скачать

Основные параметры

Чтобы обеспечивать возможность конструирования работоспособных зубчатых передач, размеры колес и шестерен, а также их прочностные и массогабаритные характеристики описываются специальными параметрами, величины которых хорошо стандартизированы ГОСТ. Так, эвольвентный профиль, положенный в основу сечения зуба подавляющего большинства колес, характеризуется модулем зацепления и имеющимся количеством зубьев на колесе или шестерне. Довольно часто, эвольвентные зубчатые колеса, имея один и тот же диаметр, могут иметь существенно различающие значения данных величин. Окружной модуль, служащий основной характеристикой для зубьев, по стандарту может иметь значения в диапазоне от 0,05 до 100 мм. Главными параметрами геометрии у различных зубчатых колес являются следующие диаметры: начальный, основной и делительный. Шагом зубчатого колеса называется общее расстояние ширины зуба и впадины. Так же важным параметром является радиус колеса. Радиуса зубчатых колес делятся: радиус окружности вершин, радиус делительной окружности, радиус основной окружности, радиус окружности впадин.

Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Диаметры окружностей

Зубчатое колесо описывается несколькими окружностями, являющимися важными характеристиками их геометрии. Так, диаметр вершин дает максимальные размеры зубчатого колеса. Ему противоположен диаметр окружности впадин. Высчитав разность между этими двумя величинами и разделив ее пополам, получим полную длину зуба. Важным параметром считается диаметр делительной окружности, имеющий формулу d=pz/3,14, по нему можно определить окружной шаг p расположенных на колесе зубьев, иначе называемый шагом зацепления, имеющий геометрический смысл части длины этой окружности, приходящейся на каждый зуб. В общем случае, диаметр делительной окружности отделяет высоту головок и высоту ножек зуба. Он также задает кривую, являющуюся необходимой базой для построения самой эвольвенты, и используется для построения требуемого в конкретной задаче профиля зубьев колес и шестерен.

Видео:Ответы на вопросы по листу №3 ТММСкачать

Модули зубчатых колес

Чтобы упростить расчеты элементов, использующихся для зацепления, для зубчатых колес была введена стандартизованная ГОСТ величина, названная модулем. Модуль зубчатого колеса является частью от диаметра имеющейся делительной окружности зубчатого колеса, которая приходится на зуб: m=d/z. Таким образом, количество зубьев колеса, его собственный делительный диаметр и его модуль — во взаимовлиянии. Модуль можно расписать как отношение шага зацепления колеса и числа Пи: m=d/3,14. Когда передаваемая зубчатыми колесами нагрузка невелика, то лучше использовать малые модули. Малый модуль дает более длительный срок эксплуатации и упрощается обработка зубчатых колес. В данном случае на делительном диаметре разместится больше зубьев, а значит и зацепление будет происходить с большим их числом, что уменьшит нагрузку на отдельные зубья шестерен. У прямозубых цилиндрических колес бывает всего только один модуль, у косозубых — два: нормальный и окружной. В расчетах используют первый.

Видео:Производство зубчатого колеса с внутренним зацеплением методом долбленияСкачать

Расчет параметров

Для всех зубчатых колес инженерный расчет их параметров является задачей комплексной, в ходе решения которой принимается во внимание конструкция всей передачи. Вначале нужно определиться с числом зубьев и необходимым в задаче модулем зацепления. Для выбора последнего необходимы параметры прочности и предполагаемого срока службы колес; материала, из которого оно будет изготовлено. На основе этих данных рассчитывается минимально возможная в данной задаче величина модуля зацепления, которое затем приводится к стандартизованным значениям, находящимся из соответствующих таблиц. Передаточное отношение высчитывается с применением формулы u=z₂z₁, где z₂ — это количество колесных зубьев, а z₁ — количество зубьев, находящихся на шестерне. Оно позволяет понять, сколько всего нужно зубьев на колесах, подлежащих сопряжению. Зная модули и полученное число зубьев для всех колес и шестерней, можно произвести дальнейшие расчеты размеров требуемых деталей, используя стандартный метод для их расчетов.

Видео:SolidWorks. Создание параметрического зубчатого колесаСкачать

Применение

Каждый из видов передач имеет свои преимущества и отрицательные качества. Нарезание прямозубых колес — довольно простой технологический процесс, поэтому они широко применяются в промышленности. Косозубые, как и прямозубые цилиндрические колеса, используются в тракторах, станках, коробках передач автотранспорта. Цилиндрические колеса с использованием внутреннего зацепления, благодаря компактности и прочности, нашли себя в самолетах, трансмиссиях автомобилей, редукторах, в шлицевых соединениях и сложных планетарных передачах, которые славятся своим особенно малым весом и габаритными размерами. При этом они предоставляют высокие передаточные числа и значительно сниженные уровни шумов при своей работе. Шевронные колеса, будучи трудоемкими в производстве, используются в больших редукторах и их ремонте, где требуется плавная и бесшумная передача значительных нагрузок. Конические колеса с нулевым наклоном и их прямозубые аналоги, имея высокую компактность и невысокую себестоимость изготовления, эксплуатируются в дифференциалах автомашин и станков. Криволинейные зубья обеспечивают коническим колесам особую прочность и малошумность, поэтому их можно найти в ответственных и скоростных передачах. Их используют практически везде: от самолетов до тракторов. Гипоидные зубчатые пары можно делать с большим передаточными числами (до 100:1), они часто используются в металлорежущем оборудовании.

Видео:КПД эвольвентного прямозубого зацепления. (Excel-калькулятор).Скачать

Зубчатое колесо и шестерня — отличия

Главными деталями в зубчатой передаче – зубчатое колесо и шестерня. Они применяются во многих промышленных узлах, машинах. Многие полагают, что зубчатое колесо и шестерня это одна и та же деталь и у них нет различий между собой. Специалисты, которые тесно связаны с промышленностью и машиностроением так не считают и уверяю, что это разные детали хоть и выполняют по сути одну и ту же функцию передачу вращательного движения. Давайте разберем основные моменты по данному вопросу.

Видео:6.3 Зубчатые цилиндрические передачиСкачать

Особенности зубчатых колес и шестерней

Внешне зубчатое колесо и шестерня имеют схожесть в виде диска с расположенными на нем зубцами. Их расположение может быть как на конической, так и цилиндрической поверхности. Основной задачей данных деталей является передача крутящего момента. Для того чтобы получить и передать крутящий момент, нужна ответная шестерня, то есть пара. Мы разобрали выше, что существует ведомая деталь и ведущая. С ведущей начинается движение и дальнейшая передача крутящего момента на ведомую деталь. В этом ключевом моменте и есть отличие зубчатого колеса от шестерни, ведущая деталь является шестерней, а ведомая зубчатым колесом. Получается, что вся разница между ними в том какую роль в механизме выполняет деталь.

Отметим что при работе двух зубчатых колес, колесо, которое имеет большее количество зубьев, называют шестерней. В ГОСТ 16530-83 есть пояснение, что зубчатое колесо и шестерня являются словами синонимами, шестерня является главным и ведущим зубчатым колесом. Существуют специалисты работающие в определенных областях промышленности и машиностроения, которые четко разделяют разницу между зубчатым колесом и шестерней. Они убеждены, что изготовление зубчатых колес это одно, а производство шестерней это другое, так как между ними есть различия.

Видео:Зубчатые передачиСкачать

Почему вам стоит обращаться в нашу компанию

Наша компания работает на своих станочных мощностях, что позволяет выполнять работы не только быстрее посредников, но и с более выгодными условиями на изготовление червячных зубчатых колес.

Работаем с любыми видами стали:

• Черные виды сталей;
• Цветные стали;
• Нержавеющие стали;
• Чугун.

Мы оказываем полный спектр услуг по металлообработке на современном, точном оборудовании с помощью качественного режущего инструмента, что позволяет нашим специалистам получать максимальной точности детали с чертежом заказчика.

🔍 Видео

Форма зубьев колеса в зависимости от коэффициента смещенияСкачать

Синтез эвольвентного зубчатого зацепленияСкачать

Механические передачи. Часть 1. История. Геометрия зубчатых колесСкачать

Практика_№14_Синтез эвольвентного зацепленияСкачать

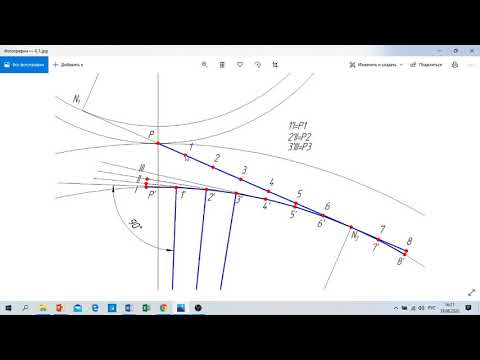
SolidWorks. Создание чертежа зубчатого колеса со смещениемСкачать

Виды зубчатых колес. Характеристика и классификация шестеренСкачать