Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать
Определение окружности, описанной около треугольника
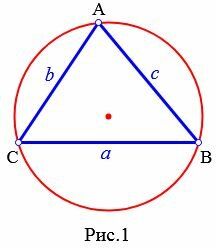
Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).
 |
При этом треугольник называется треугольником вписанным в окружность .
Видео:Центр окружности описанной вокруг треугольникаСкачать
Теорема об окружности, описанной около треугольника
Теорема 1. Около любого треугольника можно описать окружность.
 |
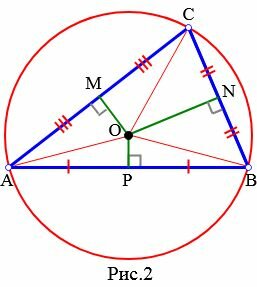Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.
Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.
Замечание 1. Около любого треугольника можно описать только одну окружность.
Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.
Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать
Центр описанной окружности
Где находится центр описанной около треугольника окружности? Что можно сказать о центре окружности, описанной около многоугольника?
Центр описанной около треугольника окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.
окружность (O;R) — описанная около ∆ ABC.
O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.
Соединим отрезками точки O и A, O и C.
OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).
По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):
Следовательно, центр описанной окружности — точка O — лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину, то есть на серединном перпендикуляре к AC.
Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.
Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то точка O — центр описанной около треугольника ABC окружности.
Что и требовалось доказать.
Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.
Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.
Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать
2 Comments
на мой взгляд у вас опечатка — «Соединим отрезками точки O и A, O и C.
OA=OB( написано ОВ вместо ОС) (как радиусы), следовательно, треугольник AOB — равнобедренный с основанием AC (по определению).»
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать
Центр описанной окружности треугольника
Если треугольник вписан в окружность так, что его вершины располагаются на окружности, такая окружность называется описанной, а треугольник считается вписанным в данную окружность.
Центр окружности расположен в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника. Серединный перпендикуляр — прямая, которая проходит через середину отрезка, перпендикулярно ему.
Вокруг треугольника возможно описать только одну окружность.
Чтобы определить радиус R описанной окружности, необходимо произведение сторон треугольника (a × b × с) разделить на учетверенную S — площадь треугольника:
R = (a × b × с) / 4S.
Если окружность описана около равностороннего треугольника, радиус R равняется:
R = a /√3.
В том случае, когда окружность описана около прямоугольного треугольника, середина его гипотенузы (с ) является центром описанной окружности.
Радиус R составляет ½ гипотенузы: R = с/2.
Радиус окружности R также равняется медиане m, проведенной к гипотенузе: R = m.
Воспользовавшись онлайн калькулятором, вы сможете быстро и правильно определить координаты центра описанной окружности.
💡 Видео
Центр окружности, описанной около треуг ABC лежит на стороне AB Радиус равен 25 Найти AC если BC=48Скачать
найти радиус окружности, описанной вокруг треугольникаСкачать
Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать
ОГЭ 2020 задание 17Скачать
Построить описанную окружность (Задача 1)Скачать
Быстро и легко определяем центр любой окружностиСкачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать
Центр кругаСкачать
Окружность, описанная около треугольника. Как найти центр и радиус. Геометрия 7-8 классСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать
Через центр О окружности, описанной около остроугольного треугольника ДВИ МГУСкачать
4K Как найти центр окружности, how to find the center of a circleСкачать
Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать
Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать
