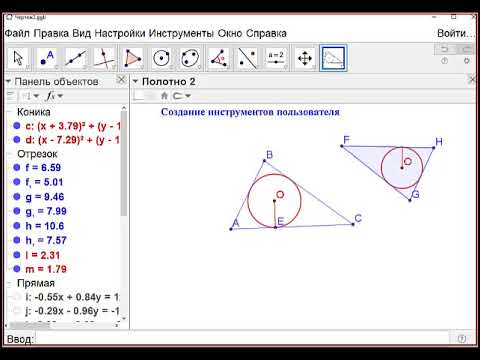
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Навигация
- Связь
- Содержание
- GeoGebra
- Основные возможности
- Как вставить апплет в веб-страницу
- Пример 1: Окружность, описанная около треугольника
- Построение с помощью мыши
- Построение с помощью поля ввода текста
- Пример 2: Касательные к окружности
- Пример 3: Производная и касательная функции
- Точка
- Ползунки
- Инструменты
- Перемещать
- Точка
- Прямая
- Перпендикулярная прямая
- Многоугольник
- Окружность по центру и точке
- Эллипс
- Отражение относительно прямой
- Текст [особые объекты]
- Текст
- Изображение
- Карандаш
- Фигура от руки
- Отношение объектов
- Использование программы «ГеоГебра» в геометрии
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- Описанные окружности в геогебре
- 🎦 Видео
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация

Связь
Содержание
Видео:Как построить вписанную в треугольник окружность с помощью программы ГЕОГЕБРАСкачать

GeoGebra
Основные возможности
Самая замечательная особенность в GeoGebra — двойное представление объектов: каждому выражению в алгебраическом окне соответствует объект в геометрическом окне и наоборот.
Возможен прямой ввод таких выражений, как
а также ряд команд, включая дифференцирование и интегрирование.
Видео:Как построить окружность, описанную около треугольника, в программе ГЕОГЕБРАСкачать

Как вставить апплет в веб-страницу
В режиме учителя выбрать апплет и нажать кнопку «Embed». Скопировать код.
Dokuwiki: вставить в страницу, окружив тегами ..
WordPress: аналогично yuotube. Под спойлором не работает. Не показывает ползунки, глючит. Возможно, надо сменить версию WordPress.
Видео:Вписанная окружность. Geogebra. ToolsСкачать
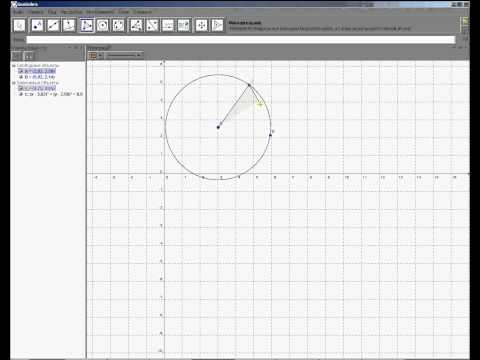
Пример 1: Окружность, описанная около треугольника
Построение с помощью мыши
Меню «Вид — Протокол построения» выводит таблицу, с перечислением всех шагов, которые вы совершили при построении. Это позволяет вам сделать заново построение шаг за шагом при помощи клавиш со стрелками, а также изменить порядок различных шагов (см. меню «Помощь» протокола построения).
Построение с помощью поля ввода текста
Создадим новое окно и введем следующие команды, нажимая ENTER после каждой строки:
Клик по иконке «Ввод» (внизу слева) активирует режим «Поле ввода». В этом режиме вы можете нажать на объект в алгебраическом или графическом окне, чтобы скопировать его имя в поле ввода текста.
Наилучшие результаты вы получите, объединив преимущества обоих способов ввода: с помощью мыши и поля ввода текста.
Видео:ОГЭ. ЕГЭ. Как построить окружность, описанную около треугольника, в программе ГЕОГЕБРАСкачать

Пример 2: Касательные к окружности
Используя GeoGebra, постройте окружность
c: (x — 3)² + (y — 2)² = 25
и её касательные через точку A = (11, 4).
Попробуйте также переместить окружность cС и посмотрите на его уравнение в алгебраическом окне. Можно изменить уравнение окружности непосредственно в алгебраическом окне, дважды кликнув по нём.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Пример 3: Производная и касательная функции
Постройте функцию f(x) = sin(x), её производную и касательную к точке на функции, а также треугольник наклона касательной.
Введите другую функцию, например f(x) = x³ — 2x², в поле ввода текста; сразу же её производная и касательная будут отображены.
Выберите режим «Перемещение» и переместите график с помощью мыши. Наблюдайте за изменением уравнения функции и ее производной.
Попробуйте также команду Интеграл[f]
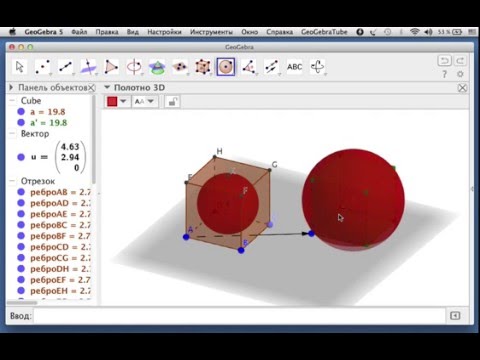
Видео:GeoGebra: сфера, вписанная в куб, и сфера, описанная около кубаСкачать
Точка
Точка задается в зависимости от настроек, по умолчанию T = (x,y) . Здесь вместо координат x, y могут быть числовые константы или другие переменные: T = (3,f(a)) .
Обратная операция — получение абсциссы точки B = (x(T), s) , и аналогично получение ординаты С = (5, y(T)) . Поэтому x,y,z не нужно использовать для именования объектов.
Длина отрезка: Расстояние[M, C]
Видео:Вписанная и описанная окружностиСкачать

Ползунки
Ползунок можно создать как с клавиатуры: ввести a=2 и затем выбрать «Показывать объект», так и с помощью инструмента Ползунок. Вы можете изменять значение ползунка, передвигая его мышью или нажимая клавиши со стрелками.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Инструменты
Перемещать
Точка
Прямая
Перпендикулярная прямая
Многоугольник
Окружность по центру и точке
Эллипс
Отражение относительно прямой
Текст [особые объекты]
Текст
Добавить на чертеж текст. Можно писать обычный текст или формулы LaTeX. Можно привязать к определенной точке на чертеже или к месту на листе, абсолютно или относительно — см. свойства.
The text you type directly in the Edit field is considered as static, i.e. it’s not affected by the objects modifications. Для создания динамического текста which displays the changing values of an object, выберите объект из списка объектов. Имя объекта заключается в grey box, in the Edit field, and its value is displayed in the Preview box. Right-clicking on the grey box allows you to select «Definition» or «Value» for each dynamic object.
Можно выполнять algebraic operations or apply specific commands to these objects, just clicking in the grey box and typing the algebraic operation or GeoGebra text command desired. The results of these operations will be dynamically shown in the resulting text.
Изображение
Добавить на чертеж картинку из файла. Можно регулировать прозрачность. Можно сделать фоновым — тогда сетка просвечивает через рисунок.
Карандаш
Можно писать как ручкой
Фигура от руки
Можно нарисовать эскиз фигуры, программа пытается угадать что нарисовано и преобразовать. Функции, отрезки, многоугольники и окружности. Для функций поддерживается Integral, но не поддерживается производная и наклон касательной.
Отношение объектов
Выбрать два объекта — выдает сообщение о равенстве величин, и о идентичности этих объектов.
Видео:Радиус описанной окружностиСкачать

Использование программы «ГеоГебра» в геометрии
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Тема урока: Описанная и вписанная окружности около треугольника
Тип урока: изучение нового учебного материала.
Предметные — познакомить учащихся с понятиями вписанной и описанной окружностей треугольника и их свойствами.
Личностные — формировать интерес к изучению темы и желание применять приобретённые знания и умения.
Метапредметные — формировать умение использовать приобретённые знания в практической деятельности.
I .Организационный момент.
( Проверка домашнего задания, наличия учебников и тетрадей. Урок проводится с помощью презентации ).
Устный опрос. 1) Что такое окружность?
2) Дайте определение треугольника?
3) Что такое перпендикуляр?
4) Что такое серединный перпендикуляр?
5) Что такое касательная?
6) Что такое биссектриса треугольника?
III. Постановка цели и задач урока. Мотивация учебной деятельности .
IV . Изучение нового материала.
Определение: Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
Говорят также, что треугольник вписан в окружность.
Теорема 21.1 Около любого треугольника можно описать окружность.
Сейчас мы сделаем чертеж в тетради, а немного позже всё сделаем с помощью программы Геогебра.
Практическая работа. Построить произвольный треугольник АВС. Провести серединные перпендикуляры m и n и k к сторонам АВ, АС и ВС соответственно. Что можно сказать о взаимном расположении серединных перпендикуляров?
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Обозначить точку пересечения буквой О. Т. к. точка О принадлежит серединному перпендикуляру m , то ОА=ОВ. Поскольку точка О принадлежит серединному перпендикуляру n , то ОА=ОС. Значит ОА=ОС=ОВ, т. е. тоска О равноудалена от всех вершин треугольника.
Около треугольника можно описать только одну окружность, т. к. серединные перпендикуляры имеют только одну точку пересечения.
Провести окружность с центром в точку О. Что можно сказать о взаимном расположении треугольника и окружности?.
Следствие 2. Центр окружности, описанной около треугольника, – это точка пересечения серединных перпендикуляров его сторон.
Определение: Окружность называют вписанной в треугольник, если она касается всех его сторон.
В этом случае также говорят, что треугольник описан около окружности.
Точка О (рис. 301) — центр вписанной окружности треугольника АВС, отрезки ОМ, ON, OP — радиусы, проведённые в точки касания,
ОМAB, ON ВС, OPAC. Поскольку ОМ = ON=OP, то центр вписанной окружности треугольника равноудалён от всех его сторон.
Теорема 21.2 В любой треугольник можно вписать окружность.
Практическая работа. Построить произвольный треугольник АВС. Провести биссектрисы углов А и В., Обозначить точку их пересечения буквой О. Т. к. точка О принадлежит биссектрисе угла А, то она равноудалена от сторон АВ и АС.(теорема 19.2). Аналогично, так как точка О принадлежит биссектрисе угла В, то она равноудалена от сторон ВА и ВС. Следовательно, точка О равноудалена от всех сторон треугольника.
Заметим, что в треугольник можно вписать только одну окружность.
Это следует из того, что биссектрисы углов А и В (см. рис. 302) пересекаются только в одной точке. Следовательно, существует только одна точка,
равноудалённая от сторон треугольника.
Следствие 1. Биссектрисы углов треугольника пересекаются в одной
точке.
Следствие 2.Центр окружности, вписанной в треугольник, — это точка
пересечения его биссектрис.
V . Первичное закрепление нового материала.
Теперь давайте попробуем сделать практическое задание с использованием программы ГеоГебра.
Задание . Изобразите окружность, описанную около треугольника (ее можно построить двумя способами).
Так же мы с вами увидим, что если вы правильно впишите треугольник в окружность, или наоборот, опишите его возле окружности, то при передвижении его он так же останется вписанным (описанным)
Примечание : Построение треугольника ABC и описанной окружности с использованием GeoGebra.
Первый способ построения с использованием мыши:
1. На панели инструментов выберите « Многоугольник » . Щёлкните левой кнопкой мыши три раза в разные места на графическое представление, у вас отметятся три точки A, B, C. Щёлкните левой кнопкой мыши в точку А и вы получите треугольник.
2. Выберите на панели инструментов « Серединный перпендикуляр » (нажмите левой кнопкой мыши на небольшой треугольник в четвёртой иконке слева) и постройте два серединных перпендикуляра нажав на две стороны треугольника.
3. Выберите на панели инструментов « Пересечение двух объектов » (вторая иконка слева). Нажмите на пересечение двух серединных
перпендикуляров или на каждый из перпендикуляров по очереди. Мы получим центр окружности.
4. Выберите « Окружность по центру и точке » . Нажмите на точку пересечения двух серединных перпендикуляров и вершину треугольника.
5. Выберите « Перемещать » на панели инструментов и используя мышь вы можете изменить треугольник, а вмести с ним будет изменяться и весь чертёж.
Второй способ построения с использованием строки ввода:
Наберите следующие команды в строку ввода внизу экрана и нажмите клавишу Enter после каждого ввода. То
Видео:Geogebra. Построение окружности и сектораСкачать
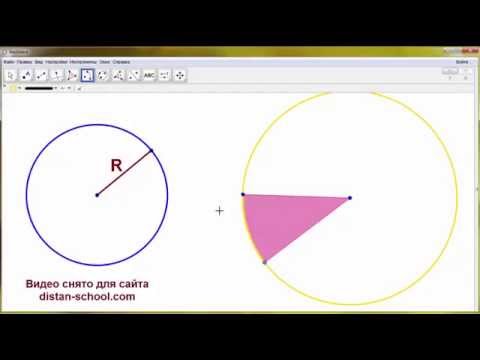
Описанные окружности в геогебре
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №24»
«Окружность»
с применением интерактивной геометрической среды GeoGebra
7 класс
Яблочкина Ольга Анатольевна
первой квалификационной категории
Цель урока:
ü познакомить с понятием окружность и ее элементами.
Задачи урока:
образовательные:
ü определять на чертеже элементы окружности;
ü Знать связь между радиусом и диаметром;
ü научиться строить окружность разными инструментами ИГС GeoGebra;
развивающие:
ü развить творческую и мыслительную деятельность учащихся;
ü формировать умение четко и ясно излагать свои мысли
воспитательные:
ü прививать аккуратность в выполнении чертежей,
ü воспитывать познавательный интерес к предмету и самостоятельности в суждениях,
ü Воспитать умение работать в паре;
ü Воспитать интерес к истории математики как науки.
Форма обучения: индивидуальная, работа в парах, фронтальная, тестовый контроль.
Методы контроля: индивидуальная, фронтальная
Оборудование: компьютер, проектор, компьютерный класс, презентация к уроку: презентация учителя, рабочая тетрадь ученика.
План урока:
- Организационный момент.
- Целеполагание. Мотивация
- Актуализация знаний
- Графический диктант
- Решение практических задач.
- Самостоятельная работа.
- Домашнее задание
- Итоги урока.
- 1.Организационный момент.
- 2.Целеполагание. Мотивация.
- 3.Актуализация знаний
- Верно ли, что все радиусы данной окружности равны?
- Верно ли, что радиус окружности является ее хордой?
- Верно ли, что диаметр окружности в 2 раза меньше радиуса?
- Верно ли, что расстояние между двумя точками окружности есть радиус?
- Верно ли, что в окружности можно провести только один радиус?
- Атанасян Л.С. и др. Геометрия 7-9 кл. – М.: Просвещение, 2006.
- Савченко Е.М. «Уроки геометрии с применением информационных технологий. 7-9 кл.». Методическое пособие с электронным приложением., 2011 г.
- Анохина Н.Е, Павлова М.А. Рабочая терадь «Наглядная планиметрия с GeoGebra 6 кл.», 2014г.
🎦 Видео
ГеоГебра для учителей. Занятие 1. Динамическая планиметрияСкачать
5 ОПИСАННАЯ ОКРУЖНСкачать
Geogebra. Часть 4Скачать

Описанная окружностьСкачать
Числовая спираль в ГеогебреСкачать
Вписанная и описанная окружности. ЗадачиСкачать

Построить описанную окружность (Задача 1)Скачать

Создание инструмента пользователя в GeoGebraСкачать