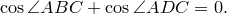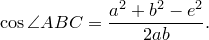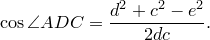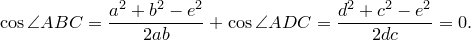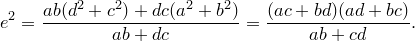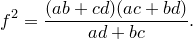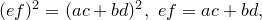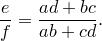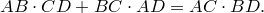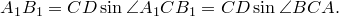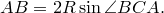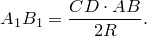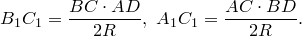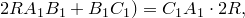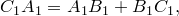Окружность

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки ( секущая ).
2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB .

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

1. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.

Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, равен 90°.

Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Видео:Основные свойства окружности. Формулы связанные с окружностьюСкачать

Длины и площади

1. Длина окружности C радиуса R вычисляется по формуле:

Площадь S круга радиуса R вычисляется по формуле:

Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле:

Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения биссектристреугольника, ее радиус r вычисляется по формуле:

где S — площадь треугольника, а — полупериметр;

центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле:

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника;

Окружность и четырехугольники

• около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:

• около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
• около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
• в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Что такое окружность: определение, свойства, формулы

В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.

Видео:Окружность и ее свойства (bezbotvy)Скачать

Определение окружности

Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.

Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.

Диаметр окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.

Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).

Видео:Окружность. 7 класс.Скачать

Свойства окружности

Свойство 1

Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.

Свойство 2

Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.

Свойство 3

Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы

1. Диаметр окружности (d):

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Разные виды окружностей и теоремы, с ними связанные.

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости,расположенных на заданном расстоянии от данной точки

Вписанная и описанная окружность, формулы для вычисления радиусов, площадей.

Окружность Аполлония — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная, не равная единице.

Биполярные координаты — ортогональная система координат на плоскости, основанная на кругах Аполлония.

Пусть на плоскости даны две точки A и B. Рассмотрим все точки P этой плоскости, для каждой из которых

где k — фиксированное положительное число. При k = 1 эти точки заполняют срединный перпендикуляр к отрезку AB; в остальных случаях указанное геометрическое место — окружность, называемая окружностью Аполлония.

Просмотр содержимого документа
«Разные виды окружностей и теоремы, с ними связанные.»

“А в окружность я влюбился и на ней остановился.”

Цель проекта: Изучить свойства, виды разных окружностей и теоремы, с ними связанные.

Я начал свою работу с того , что изучил свойства окружности в школьном курсе геометрии по учебнику А.В.Погорелова “Геометрия 7-9” и материал за рамками школьного курса. При сборе информации из различных источников и в работе над проектом я расширил свои знания и буду продолжать дальше изучать эту тему и делиться знаниями с одноклассниками и всеми , кому это интересно.

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом. Замкнутый круг, не имеющий внутренное пространство.

Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)

Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.

Окружность называется единичной, если ее радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Клавдий Птолемей (), живший в конце первого — начале второго века н.э., был древнегреческим ученым-астрономом, математиком, астрологом, географом, оптиком и теоретиком музыки. Он известен как комментатор Евклида. Птолемей пытался доказать знаменитый Пятый постулат. Основной труд Птолемея — “Альмагест”, в котором он изложил сведения по астрономии. Включал “Альмагест” и каталог звездного неба.

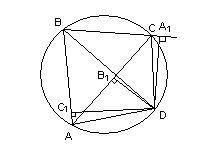
Теорема Птолемея. Вокруг четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений его противоположных сторон.

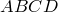
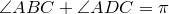
Доказательство необходимости. Поскольку четырехугольник вписан в окружность, то

, откуда

Из треугольника 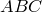по теореме косинусов находим

Аналогично из треугольника :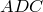

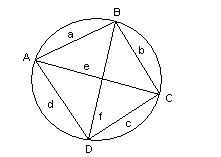
Сумма этих косинусов равна нулю:

Отсюда выразим :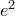

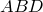
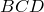
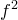
Рассмотрим треугольники и и найдем :

что и требовалось доказать.

Попутно мы доказали еще одно утверждение. Для четырехугольника, вписанного в окружность,

Доказательство достаточности. Пусть выполнено равенство

Докажем, что вокруг четырехугольника 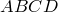можно описать окружность.

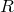
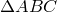
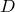
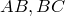
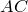
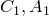
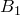
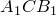
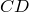
Обозначим через радиус окружности, описанной вокруг . Из точки опустим перпендикуляры на прямые и и обозначим точки пересечения этих прямых и перпендикуляров к ним через и соответственно. По теореме синсов для треугольника получаем (диаметр описанной окружности для этого треугольника равен ):

По теореме синусов для треугольника 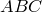имеем

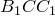
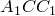
Таким же образом, рассматривая треугольники и получим соотношения

Отсюда, подставляя эти выражения в исходное равенство, имеем

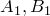
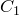
откуда следует, что точки и лежат на одной прямой.

Докажем теперь, что из этого следует, что вокруг четырехугольника 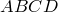можно описать окружность (достаточное условие теоремы Симсона).

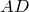
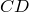
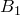
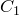
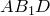
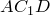
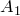
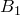
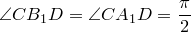
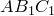
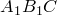
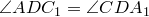
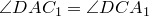
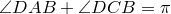
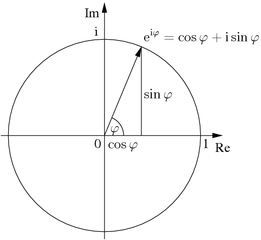
Построим окружности на отрезках и как на диаметрах. Первая из них проходит через точки и (углы и прямые), а вторая — через точки и (). Углы и равны как вертикальные, откуда следует, что , а значит, и . Отсюда , и вокруг четырехугольника можно описать окружность.

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

,

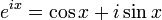
где e — основание натурального логарифма,

i — мнимая единица.

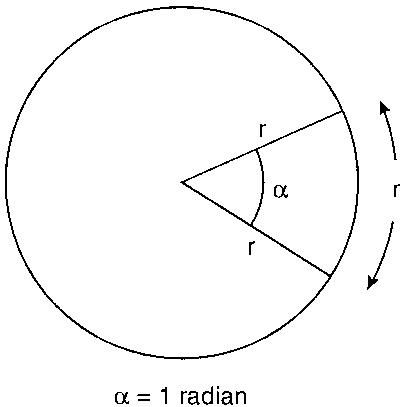
Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан.

Длина единичной полуокружности обозначается через π.

📽️ Видео

Важные свойства и определения, связанные с окружностьюСкачать

7 класс, 21 урок, ОкружностьСкачать

Свойство диаметра окружности. 7 класс.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Свойства хорд, касательных, секущих окружности I Для решения задач из ОГЭ И ЕГЭ I Часть 1Скачать

Свойства хорд окружностиСкачать

Математика это не ИсламСкачать

8 класс, 32 урок, Касательная к окружностиСкачать

Угол между хордой и касательнойСкачать