Окружности в g коде (3 видео) | Курс школьной геометрии

Краткое руководство по G-Code. Круговая интерполяция G02 и G03.

Содержание

Круговая интерполяция G02 и G03 — это движение по круговой дуге
Круговое движение — это режим, инициируемый через G02 и G03
Варианты синтаксиса Arc для различных диалектов и режимов G-кода
Дроби круга, квадранты и регуляторы
Спиральная интерполяция
Круговая интерполяция (G02, G03, CIP)
Круговая и винтовая интерполяция ЧПУ Siemens Sinumerik
Круговая интерполяция
📹 Видео

Видео:G02 и G03. Круговая и винтовая интерполяция. Создание управляющей программы для ЧПУ #cncСкачать

Круговая интерполяция G02 и G03 — это движение по круговой дуге

Закончив обсуждение линейной интерполяции или движения по прямой линии, мы переходим к круговой интерполяции G02 и G03 , которая представляет собой движение по дуге окружности. За исключением довольно экзотической способности следовать «NURBS-пути», большинство контроллеров G-кода поддерживают только два вида движения: линейное и круговое. Круговая интерполяция на вашем станке немного сложнее, так как две оси должны быть точно согласованы. Рисование полного круга включает не только скоординированное движение, но и изменение направления в каждой из четырех точек квадранта. Это будут точки, соответствующие 0, 90, 180 и 270 градусам. Если у станка вообще есть люфт, он будет очевиден при этих разворотах, потому что там будет сбой в разрезе.

Видео:G-, M-КОДЫ - #25 - БАЗОВЫЕ G-КОДЫ: G00 И G01 / Программирование обработки на станках с ЧПУСкачать

Круговое движение — это режим, инициируемый через G02 и G03

Как и линейное движение (инициированное G00 и G01), круговое движение — это режим, инициированный через G02 и G03. G02 устанавливает режим для дуг окружности по часовой стрелке. G03 устанавливает режим для дуг окружности против часовой стрелки.

Определение дуги для контроллера ЧПУ

После того, как установлен режим G02 или G03, дуги определяются в G-коде путем идентификации двух конечных точек и центра, который должен быть равноудаленным от каждой конечной точки, в противном случае возникнет аварийный сигнал.

Определение центра через относительные смещения IJK

Центр чаще всего идентифицируется с помощью I, J или K для определения относительного смещения от начальной точки дуги к центру. Вот типичная дуга по часовой стрелке:

Буквы I и J указывают относительные координаты от начальной точки до центра. Другими словами, если мы добавим значение I к X начальной точки и значение J к Y начальной точки, мы получим X и Y для центра.

Определение центра через радиус с помощью «R»

Мы также можем определить центр, просто указав радиус круга. Допустим радиус нашего круга равен 2, поэтому g-код может быть простым:

Многие из вас прямо здесь и сейчас решат, что, поскольку R проще для понимания и короче для написания, вы просто собираетесь использовать R и забыть о IJK. Но мастера ЧПУ обработки советуют использовать команды IJK. Их аргумент состоит в том, что, используя IJK, вы дважды проверяете правильность дуги.

Потому что контроллер может вычислить фактический набор координат для центра через IJK. Получив координаты центра, он может проверить, что он одинаково удален от обеих конечных точек. Проверка каждого из этих двух расстояний — это двойная проверка. В случае формата «R» контроллер не имеет такой двойной проверки. Он должен выбрать центр, который гарантирует равное расстояние.

Лично я не знаю, согласен ли я с инструкторами ЧПУ в том, что это обеспечивает дополнительную проверку или нет. Я говорю, что используйте тот подход, который имеет смысл в вашей конкретной ситуации, но вы определенно должны быть знакомы с обоими. В любом случае вам нужно будет привыкнуть к относительным координатам, поскольку они чертовски удобны.

Видео:G-, M-КОДЫ - #26 - БАЗОВЫЕ G-КОДЫ: G02 И G03 / Программирование обработки на станках с ЧПУСкачать

Варианты синтаксиса Arc для различных диалектов и режимов G-кода

Это еще одно из тех мест, где происходит много непонятных вещей, например, что будет делать ваш контроллер. Обычно предполагается, что если у вас есть и IJK, и R в одном блоке, R имеет приоритет, а IJK игнорируется. Но есть контроллеры, которые работают не так, поэтому убедитесь, что вы знаете, что происходит.

Есть несколько параметров, которые определяют, как работают дуги.

Давайте рассмотрим эти варианты:

— Инкрементальный против абсолютного IJK : мы обсуждали IJK как представление координат относительно начальной точки для центра. Добавьте I к X, J к Y и K к Z начальной точки, и вы получите центр. Многие элементы управления также имеют возможность использовать IJK как абсолютные координаты центра.

— Модальные центры IJK : когда IJK являются абсолютными координатами центра, некоторые контроллеры запоминают последний определенный центр, поэтому в этом случае IJK является модальным. При использовании такой настройки управления вы можете просто продолжать вводить команды XYZ для дуг без необходимости каждый раз определять новый центр. Однако не ясно, что вы сэкономите много — как часто вы хотите делать несколько дуг с одним и тем же центром?

— Модальные центры R : Еще одна разновидность идеи модального центра состоит в том, чтобы позволить радиусу, определенному буквой «R», быть модальным. Каким бы ни был последний использованный R, контроллер запоминает и снова использует это значение, если R не задано. Это кажется более полезным, чем модальный IJK. Например, у кармана могут быть дуги для углов одинакового радиуса.

— Приоритет R : как уже упоминалось, большинство контроллеров будут использовать «R», если «R» и «IJK» указаны в одном блоке. Н

— Helical Interp. : Эта опция определяет, разрешает ли ваш контроллер спиральную интерполяцию.

Наиболее распространенная проблема при настройке постпроцессора CAM или симулятора ЧПУ: абсолютный и относительный IJK

У всех нас был опыт, когда мы смотрели на симуляцию проходов (или, что еще хуже, видели его в реальном движении инструмента, что довольно пугающе), и видели гигантские почти полные круги без каких-либо признаков знакомых движений деталей, которые мы ожидали увидеть. Вот типичный пример:

Если вы видите такие вещи, первое, что нужно проверить, — это абсолютный IJK в сравнении с относительным IJK для дуг. Настройка должна соответствовать между тем, что выдает CAM, и тем, чтополучает контроллер или симулятор.

Видео:G-коды для ЧПУ фрезера для начинающих.Скачать

Дроби круга, квадранты и регуляторы

Первое, что нужно знать о дуге, это то, что невозможно указать дугу более 360 градусов. В некоторых контроллерах для спиральной интерполяции есть некоторые исключения (см. Ниже) просто потому, что это может быть полезно для спиралей. Если требуется полный круг, установите начальную и конечную точки равными друг другу:

G02 X3.25 Y2.0 I-1.25 J0

Интересно, что вы не можете указать полный круг с помощью «R». Это связано с тем, что существует бесконечное количество кругов, которые начинаются и заканчиваются в одной и той же точке определенного радиуса, поэтому контроллер не знает, какой круг может быть правильным.

Есть еще более забавный ньюанс с «R» и более крупными дугами. Например, дуга все еще может иметь определенный радиус и по часовой стрелке (или против часовой стрелки), но центр будет разным, если вы перемещаетесь более чем на 90 градусов. Например:

Учитывая два показанных варианта, контроллер выбирает путь на основе знака радиуса. Отрицательное получает более длинную дугу, положительное — короче. Отрицательный знак заставляет контроллер искать дугу более 180 градусов.

Некоторые контроллеры еще более чувствительны и не будут программировать дугу, пересекающую линию квадранта. Следовательно, наибольший угол, по которому может следовать дуга, составляет 90 градусов, и этот угол не должен пересекать 0, 90, 180 или 270 градусов. Углы в 90 градусов, пересекающие линию квадранта, должны быть разбиты на две части, причем соединение между частями должно быть прямо на линии квадранта.

Полные круги без XYZ

Полные круги появляются, когда начальная и конечная точки идентичны, а центр указан через IJK (помните, что R ведет к бесконечному количеству кругов). Учитывая, что вы хотите, чтобы начальная и конечная точки были одинаковыми, возможно, вам не придется беспокоиться даже об указании конечной точки с помощью XYZ. Некоторым контроллерам это может потребоваться, но большинству — нет. Вот простая программа с g-кодом, которая таким образом создает 3 круга:

N45 G0 X-2. Y.75
N46 G1 Z-.5 F10.
N47 Y.5 F30. S2000
N48 G2 J-1.1
N49 G1 Y.75
N50 Z.2
N51 G0 X.75 Y-3.4
N52 G1 Z-.5 F10.
N53 X.5 F30.
N54 G2 I-1.1
N55 X.75
N56 Z.2
N57 G0 X-4.75 Y-3.4
N58 G1 Z-.5 F10.
N59 X-4.5 F30.
N60 G2 I1.1
N61 G1 X-4.75
N62 Z.2

А вот как выглядит визуализация:

Совет по упрощению программирования дуги: начните с сегментов

Когда я прокладываю траекторию инструмента, я предпочитаю оставлять дуги напоследок. Вместо каждой дуги я просто помещаю отрезок линии, конечные точки которого соответствуют конечным точкам дуги. Это позволяет быстро собрать грубый набросок траектории инструмента, и часто кажется, что легче вернуться и преобразовать линии в дуги, когда базовая структура уже установлена.

Видео:Программирование станков с ЧПУ. Урок 35. Круговая интерполяция на фрезерных станках.Скачать

Спиральная интерполяция

Спираль — это дуга, которая непрерывно движется в третьем измерении, как винтовая резьба. При винтовой интерполяции мы указываем такую дугу с помощью G02 / G03, чтобы резец перемещался по спирали. Это может быть сделано для фрезерования резьбы , интерполяции отверстия или для множества других целей. Вот диаграмма из программы резьбы 1/4 ″ NPT:

Вот пример кода программы фрезерования резьбы:

G01 G91 Z-0.6533 F100.
G01 G42 D08 X0.0235 Y-0.0939 F10.
G03 X0.0939 Y0.0939 Z0.0179 R0.0939
G03 X-0.1179 Y0.1179 Z0.0179 R0.1179
G03 X-0.1185 Y-0.1185 Z0.0179 R0.1185
G03 X0.1191 Y-0.1191 Z0.0179 R0 .1191 F16.
G03 X0.1196 Y0.1196 Z0.0179 R0.1196
G03 X-0.1202 Y0.1202 Z0.0179 R0.1202 F26.
G03 X-0.1207 Y-0.1207 Z0.0179 R0.1207
G03 X0.1213 Y-0.1213 Z0.0179 R0.1213
G03 X0.1218 Y0.1218 Z0.0179 R0.1218
G03 X-0.0975 Y0.0975 Z0.0179 R0 0,0975

Это формат «R» (радиус) для дуг, и обратите внимание, что есть координата Z, чтобы указать изменение глубины для конечной точки каждой дуги. В этом коде используется относительное движение (G91), поэтому каждый «Z0.0179» перемещает фрезу на 0,0179 дюйма глубже.

Мы вернемся к резьбофрезерованию более подробно в следующей главе, полностью посвященной этой теме. А пока мы просто хотели, чтобы вы познакомились с идеей создания спиралей, а также плоских двумерных дуг.

Создание траекторий движения инструмента понравится вашей машине

Каждый раз, когда резак меняет направление, он добавляет определенное напряжение. Резак будет врезаться в материал больше или меньше, чем был, в зависимости от того, меняется ли направление на заготовку (или неразрезанный материал) или от нее. Ваша машина будет намного счастливее, если вы запрограммируете дугу, а не резкое изменение направления по прямой. Даже дуга с очень маленьким радиусом позволит контроллеру избежать мгновенного изменения направления, что может оставить след на поверхности в лучшем случае и вызвать вибрацию или другие проблемы в худшем случае. Для небольших изменений направления это может не иметь смысла. Но чем резче изменение, тем больше вероятность, что вам следует использовать дугу для облегчения поворота.

Видео:Круговая интерполяцияСкачать

Круговая интерполяция (G02, G03, CIP)

Дата добавления: 2015-06-12 ; просмотров: 13450 ; Нарушение авторских прав

Круговая интерполяция — это согласованное движение механизмов по круговой траектории относительно двух осей. Она возможна в любой из трех координатных плоскостей XY, YZ, XZ. Для задания направления перемещения инструмента служат подготовительные функции – G02 движение по часовой стрелке или G03 движение против часовой стрелки. Для реализации круговой интерполяции СЧПУ требуется указание рабочей плоскости (G17-G19). Функции G02, G03 действует модально. Они отменяются друг другом или функциями G00 иG01

При круговой интерполяции, кроме задания координат конечной точки дуги окружности под адресами X, Y, Z, необходимо под адресами I, J, K задать координаты положения центра окружности по соответствующим осям.

Для плоскости XY — задаются адреса X, Y, I, J

Для плоскости XZ — задаются адреса X, Z, I, K

Для плоскости YZ — задаются адреса Y, Z, J, K.

Предварительные установки G90/G91 абсолютного или составного размера действуют только для конечной точки окружности. Координаты центра I, J, K стандартно вводятся в составном размере относительно начальной точки окружности. Абсолютное указание центра относительно нулевой точки детали программируется покадрово с помощью адресов: I=AC(…), J=AC(…), K=AC(…).

Если дуга программируется с центром, но без конечной точки, то получается полный круг.

Возможно несколько способов программирования обработки окружности или дуги.

Ø Программирование дуги окружности с центром и конечной точкой

Круговое движение описывается через:

— конечную точку в декартовых координатах X, Y, Z и

—

центр окружности по адресам I, J, K.

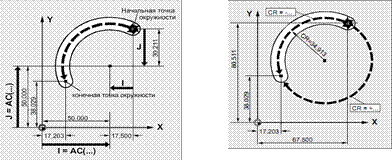
Рисунок 18 — Программирование круговой интерполяции (фрезерование)

Пример программирования фрезерной обработки (рис.18):

N10 G00 G17 G90 X67.5 Y80.211

N20 G03 X17.203 Y38.029 I–17.5 J–30.211 F500 (Координаты центра заданы относительно начальной точки)

N10 G00 X67.5 Y80.211

N20 G03 X17.203 Y38.029 I=AC(50) J=AC(50) (Координаты центра заданы относительно нуля детали в абсолютной системе координат)

Пример программирования токарной обработки (рис.13):

Рисунок 19 —

Программирование круговой интерполяции (точение)

N120 G00 X12 Z0

N125 G01 X40 Z-25 F0.2

N130 G03 X70 Z-75 I-3.335 K-29.25 (Координаты центра заданы относительно начальной точки)

N120 G00 X12 Z0

N125 G01 X40 Z-25 F0.2

N130 G03 X70 Z-75 I=AC(33.33) K=AC(-54.25) (Координаты центра заданы нуля детали в абсолютной системе координат)

Ø Программирование окружности с радиусом и конечной точкой

При этом способе программирования координаты центра не указывается. Наряду с радиусом окружности посредством знака + или – необходимо указать, должен ли угол перемещения быть больше или меньше 180°. Положительный знак не нужен. Круговое движение описывается через:

— радиус окружности CR=-…: угол меньше или равен 180°

— радиус окружности CR=…: угол больше 180°

— конечную точку в декартовых координатах X, Y, Z.

Пример программирования фрезерной обработки (рис.18,б):

N10 G00 G17 X67.5 Y80.511

N20 G03 X17.203 Y38.029 CR=-34.913

N40 M30 Конец программы

Пример программирования токарной обработки (рис.19):

N125 G1 X40 Z-25 F0.2

N130 G3 X70 Z-75 CR=-30

Полные круги (угол перемещения 360°) программируются не с помощью CR=, а через конечную точку окружности и параметры интерполяции.

Пример фрезерования кругового паза (рис.20).

Рисунок 20 — Фрезерование кругового паза

N10 G90 G00 X45 Y60 Z2 T1 S2000 M3 (Ввод абсолютного размера, перемещение на ускоренном ходу на позицию XYZ, выбор инструмента, задание скорости вращения шпинделя, вращение вправо)

N20 G01 G 94 Z-5 F500 (Подача инструмента вдоль оси Z с подачей 500 мм/мин)

N30 G02 X20 Y35 I=AC(45) J=AC(35) (Фрезерование паза по часовой стрелке с заданием центра окружности в абсолютном размере)

N30 G02 X20 Y35 I0 J-25 (Центр окружности в составном размере)

N40 G00 Z2 (Отвод инструмента на ускоренном ходу)

N50 M02 (Конец программы )

Примертокарной обработки с круговой интерполяцией (рис.21)

Рисунок 21 — Токарная обработки детали

N5 T1 S2000 M3 D1 (Инструмент, шпиндель включен вправо)

N10 G00 G90 X11 Z1 (Ввод абсолютного размера, ускоренным ходом на позицию XZ)

N20 G01 Z-15 F0.2 (Обработка цилиндрического участка)

N30 G03 X11 Z-27 I=AC(-5) K=AC(-21) (Обработка сферического участка. Центр окружности в абсолютном размере)

N30 G03 X11 Z-27 I-6 K-6 (Центр окружности в составном размере)

N40 G01 Z-40 (Обработка цилиндрического участка)

N50 M02 (Конец программы)

\|	следующая лекция ==>
Линейная интерполяция (G01)	\|	Винтовая интерполяция

Не нашли то, что искали? Google вам в помощь!

Видео:Генерирование программы (G-code) для ЧПУ для сверления отверстий, расположенных на окружностиСкачать

Круговая и винтовая интерполяция ЧПУ Siemens Sinumerik

Цель: изучить основы создания круговых перемещений в системе числового программного управления Siemens Sinumerik.

Видео:ПРОГРАММИРОВАНИЕ ТОКАРНОГО СТАНКА С ЧПУ ЗА 10 МИНУТ.Скачать

Круговая интерполяция

Круговая интерполяция задается с помощью операторов G2 и G3.

Инструмент движется от начальной точки к конечной по круговой траектории.

Направление определяется G-функцией (рисунок 3.1):

— G2 — по часовой стрелке;
— G3 — против часовой стрелки.

Рисунок 3.1 — Определение направления вращения окружности G2/G3 в 3-х

Описание необходимой окружности может задаваться различными способами (рисунок 3.2). Операторы G2/G3 действуют модально до повторного вызова через другой оператор из группы G (GO, G1. ). В таблице 3.1 приведены примеры задания окружности разными способами.

Другими возможностями программирования окружности является:

— СТ — окружность с тангенциальным примыканием;
— СТР — окружность через промежуточную точку.

Таблица 3.1 — Примеры задания окружности разными способами

Через центр и конечную точку

Через радиус окружности и конечную точку

Через аппертурный угол и центр

Через аппертурный угол и конечную точку

Через полярные координаты, окружность вокруг полюса

G2/G3 и указание радиуса (^конечная точкаЗ

G2/G3 и указание центра (+конечная точка) :

Начальная точка X. Y

G2/G3 и указание аппертурного угла Оконечная точка!-

G2/G3 и указание аппертурного угла (+цетрЗ

Начальная точка X. Y

Рисунок 3.2 — Варианты программирования окружности с G2/G3 на

примере осей X/Y

3.1.1 Допуски ввода для окружности

Окружности принимаются СЧПУ только с определенным допуском размеров. При этом сравнивается радиус окружности в начальной и конечной точке. Если разница не превышает допуска, то происходит внутренняя точная установка центра. В ином случае сигнализируется ошибка. Значение допуска может быть установлено через машинные данные.

Полные окружности в одном кадре возможны только при указании центра и конечной точки!

Для окружностей с указанием радиуса знак у CR=. служит для правильного выбора окружности. С одной и той же начальной, конечной точкой, радиусом и тем же направлением возможно 2 окружности. Отрицательный знак у CR—. определяет окружность, круговой сегмент которой больше полукруга, иначе определена окружность с круговым сегментом, меньшим или равным полукругу (рисунок 3.3).

Окружность дольше полукруга

МР1- центр окружности 1

МР2-ценпр окружности 2

Окружность меньше или радна полукругу

Рисунок 3.3 — Выбор окружности из двух возможных окружностей при указании радиуса через знак CR=

3.1.2 Примеры программирования круговой интерполяции

Рассмотрим подробно способы задания круговой интерполяции. На рисунке 3.4 приведен пример программирования через указание центра и конечной точки. На данном рисунке параметр I задает расстояние до центра окружности по оси X, а параметр J — по Y. Если направление от начальной точки к центру окружности совпадает с направлением соответствующей оси, то знак у этих параметров будет положительный, в противном случае параметры I и J имеют отрицательное значение (параметр J на рисунке 3.4).