Окружности радиусов 28 и 36 касаются внешним образом

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Сборник И.В. Ященко. Решение заданий №26..pptx

Описание презентации по отдельным слайдам:

Выбранный для просмотра документ Сборник И.В. Ященко. Тексты заданий №26..docx

Боковые стороны АВ и С D трапеции АВС D равны соответственно 36 и 39 , а основание ВС = 12. Биссектриса угла А D С проходит через середину стороны АВ. Найдите площадь трапеции.

На стороне ВС остроугольного треугольника АВС (АВ ВС) как на диаметре построена полуокружность, пересекающая высоту А D в точке М , А D = 32 , М D = 8, Н – точка пересечения высот треугольника АВС. Найдите АН.

Две касающиеся внешним образом в точке К окружности, радиусы которых равны 22 и 33, касаются сторон угла с вершиной А . Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С. Найдите радиус окружности, описанной около треугольника АВС.

В треугольнике АВС известны длины сторон АВ = 40, АС = 64, точка О – центр окружности, описанной около треугольника АВС. Прямая В D , перпендикулярная прямой АО, пересекает сторону АС в точке D . Найдите С D .

В треугольнике АВС биссектриса угла А делит высоту, проведённую из вершины В в отношении 13:12, считая от вершины В . Найдите радиус окружности, описанной около треугольника АВС , если ВС = 10 .

Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности , вписанной в треугольник ВСР , равен 96 , тангенс угла ВАС равен . Найдите радиус окружности , вписанной в треугольник АВС.

Биссектрисы углов А и В при боковой стороне АВ трапеции АВС D пересекаются в точке F . Найдите АВ , если А F = 24 , В F = 10 .

Биссектрисы углов С и D при боковой стороне С D трапеции АВС D пересекаются в точке G . Найдите С D , если С G = 24 , DG = 18 .

Биссектрисы углов А и В при боковой стороне АВ трапеции АВС D пересекаются в точке F . Биссектрисы углов С и D при боковой стороне С D пересекаются в точке G . Найдите FG , если основания равны 16 и 30 , боковые стороны – 13 и 15 .

Биссектрисы углов А и В при боковой стороне АВ трапеции АВС D пересекаются в точке F . Биссектрисы углов С и D при боковой стороне С D пересекаются в точке G . Найдите FG , если средняя линия трапеции равна 21, боковые стороны – 13 и 15 .

Биссектрисы углов А и В при боковой стороне АВ трапеции АВС D пересекаются в точке F . Биссектрисы углов С и D при боковой стороне С D пересекаются в точке G . Найдите FG , если средняя линия трапеции равна 19, боковые стороны – 13 и 15 .

В треугольнике АВС биссектриса ВЕ и медиана А D перпендикулярны и имеют одинаковую длину , равную 28. Найдите стороны треугольника АВС .

В треугольнике АВС биссектриса ВЕ и медиана А D перпендикулярны и имеют одинаковую длину , равную 64 . Найдите стороны треугольника АВС .

В выпуклом четырёхугольнике АВС D отмечены точки K , L , M и N — середины сторон А D , АВ , ВС и С D соответственно . Расстояние между точками К и L равно 6 , между точками К и N — 12 . Найдите периметр четырёхугольника KLMN .

В выпуклом четырёхугольнике АВС D отмечены точки K , L , M и N — середины сторон А D , АВ , ВС и С D соответственно . Расстояние между точками К и L равно 8 , между точками К и N — 14 . Найдите площадь четырёхугольника KLMN , если диагонали АС и В D образуют угол 30° .

В выпуклом четырёхугольнике АВС D отмечены точки K , L , M и N — середины сторон А D , АВ , ВС и С D соответственно . Найдите отношение площади четырёхугольника АВС D к площади четырёхугольника KLMN .

Окружности радиусов 12 и 52 касаются внешним образом. Точки А и В лежат на первой окружности , точки С и D — на второй . При этом АС и В D — общие касательные окружностей . Найдите расстояние между прямыми АВ и С D .

Окружности радиусов 15 и 21 касаются внешним образом. Точки А и В лежат на первой окружности , точки С и D — на второй . При этом АС и В D — общие касательные окружностей . Найдите расстояние между прямыми АВ и С D .

Окружности радиусов 36 и 45 касаются внешним образом. Точки А и В лежат на первой окружности , точки С и D — на второй . При этом АС и В D — общие касательные окружностей . Найдите расстояние между прямыми АВ и С D .

Две касающиеся внешним образом в точке К окружности , радиусы которых равны 39 и 42 , касаются сторон угла с вершиной А . Общая касательная к этим окружностям , проходящая через точку К , пересекает стороны угла в точках В и С . Найдите радиус окружности , описанной около треугольника АВС .

Две касающиеся внешним образом в точке К окружности , радиусы которых равны 36 и 39 , касаются сторон угла с вершиной А . Общая касательная к этим окружностям , проходящая через точку К , пересекает стороны угла в точках В и С . Найдите радиус окружности , описанной около треугольника АВС .

Найдите площадь трапеции , диагонали которой равны 15 и 9 , а средняя линия равна 6 .

Найдите площадь трапеции , диагонали которой равны 15 и 7 , а средняя линия равна 10 .

Найдите площадь трапеции , диагонали которой равны 10 и 8 , а средняя линия равна 3 .

Площадь треугольника АВС равна 80 . Биссектриса А D пересекает медиану ВК в точке Е , при этом В D : С D = 1 : 3 . Найдите площадь четырёхугольника ED СК .

Площадь треугольника АВС равна 60 . Биссектриса А D пересекает медиану ВК в точке Е , при этом В D : С D = 1 : 2 . Найдите площадь четырёхугольника ED СК .

В трапеции АВС D боковая сторона АВ перпендикулярна основанию ВС . Окружность проходит через точки С и D и касается прямой АВ в точке Е . Найдите расстояние от точки Е до прямой С D , если А D = 15 , ВС = 12 .

В трапеции АВС D боковая сторона АВ перпендикулярна основанию ВС . Окружность проходит через точки С и D и касается прямой АВ в точке Е . Найдите расстояние от точки Е до прямой С D , если А D = 6 , ВС = 5 .

Боковые стороны АВ и С D трапеции АВС D равны соответственно 20 и 25 , а основание ВС равно 5 . Биссектриса угла А D С проходит через середину стороны АВ. Найдите площадь трапеции .

Боковые стороны АВ и С D трапеции АВС D равны соответственно 18 и 30 , а основание ВС равно 3 . Биссектриса угла А D С проходит через середину стороны АВ. Найдите площадь трапеции .

Боковые стороны АВ и С D трапеции АВС D равны соответственно 40 и 41 , а основание ВС равно 16 . Биссектриса угла А D С проходит через середину стороны АВ. Найдите площадь трапеции .

Биссектриса угла А треугольника АВС делит медиану , проведённую из вершины В , в отношении 5 : 4 , считая от вершины В . В каком отношении , считая от вершины С , эта биссектриса делит медиану , проведённую из вершины С ?

Биссектриса угла В треугольника АВС делит медиану , проведённую из вершины С , в отношении 7 : 2 , считая от вершины С . В каком отношении , считая от вершины А , эта биссектриса делит медиану , проведённую из вершины А ?

Углы при одном из оснований трапеции равны 56° и 34° , а отрезки , соединяющие середины противоположных сторон трапеции , равны 16 и 13 . Найдите основания трапеции .

Углы при одном из оснований трапеции равны 27° и 63° , а отрезки , соединяющие середины противоположных сторон трапеции , равны 13 и 10 . Найдите основания трапеции .

Углы при одном из оснований трапеции равны 53° и 37° , а отрезки , соединяющие середины противоположных сторон трапеции , равны 6 и 2 . Найдите основания трапеции .

Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?

Геометрия | 5 — 9 классы

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Расстояние между центрами О1 и О2 окружностей равно 36 + 45 = 81.

Из центра меньшей окружности проведём отрезок параллельно касательной до радиуса в точку касания большей окружности.

Синус угла между этим отрезком и линией О1О2 равен(45 — 36) / 81 = 9 / 81 = 1 / 9.

Этот угол равен углам между АВ и СД и радиусами в точки касания.

Тогда искомое расстояние L между АВ и СД равно :

L = 81 — 45 * (1 / 9) + 36 * (1 / 9) = 81 — 5 + 4 = 80.

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Окружности радиусов 12 и 20 касаются внешним образом?

Окружности радиусов 12 и 20 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и D — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Видео:ОГЭ 2024 Ященко 14 вариант ФИПИ школе полный разбор!Скачать

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C?

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C.

Прямая AB касается окружности меньшего радиуса в точке A, а другой — точке B.

Через точку C проведена касательная, которая пересекает прямую AB в точке D.

А) Докажите, что вокруг четырёхугольника AOCD можно описать окружность

б) Найдите радиус этой окружности.

Видео:Две окружности разных радиусов касаются внешним образом в точке КСкачать

Окружности радиусов 45 и 90 касаются внешним образом?

Окружности радиусов 45 и 90 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D на второй .

При этом AC и BD – общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:ОГЭ 2024 Ященко 13 вариант ФИПИ школе полный разбор!Скачать

Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К?

Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К.

Найдите расстояние от точки А до ближайшей к ней точки окружности, если АК = 4.

Видео:ОГЭ по математике. 9 класс. Задача 26. Вариант 5.Скачать

Решите пожалуйста?

Две окружности разных радиусов касаются друг друга внешним образом.

Две их общие касательные, которые не проходят через точку касания окружностей, касаются окружности меньшего радиуса в точках A и B, а окружности большего радиуса — в точках C и D.

При этом точки A и C лежат на одной касательной, а B и D на другой касательной.

Найдите расстояние между прямыми AB и CD, если радиусы окружностей равны 1, 5 и 6.

Видео:Разбор 3 варианта из сборника Ященко. Зонты | Математика ОГЭ 2023 | УмскулСкачать

Справедливы ли данные суждения?

Справедливы ли данные суждения?

1. Если прямая касательная окружности, то она имеет две общие точки с окружностью.

Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

Прямая и окружность могут иметь только две общие точки.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

О₁ и О₂ — центры двух касающихся внешнем образом окружностей?

О₁ и О₂ — центры двух касающихся внешнем образом окружностей.

Прямая О₁О₂ пересекает первую окружность (с центром в точке О₁) в точке А.

Определите диаметр второй окружности, если радиус первой равен 5 см, а касательная, проведенная из точки А ко второй окружности, образует с прямой О₁О₂ угол в 30ᵒ.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А?

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.

Найдите расстояние от точки В до окружности, если длина касательной равна 12 см.

С рисунком, пожалуйста.

Видео:Две касающиеся внешним образом в точке А окружности, радиусы которых равны 4 и 8Скачать

Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью?

Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью.

Построить окружность, которая касается прямой l и касается окружности в точке А.

Видео:ОГЭ 2023 Ященко 2 вариант ФИПИ школе полный разбор!Скачать

Окружности с радиусами, равными 4 см и 1 см, внутренне касаются?

Окружности с радиусами, равными 4 см и 1 см, внутренне касаются.

Хорда АВ большей окружности касается меньшей окружности, и прямая АВ образует с общей касательной в окружности угол 60°.

Вы зашли на страницу вопроса Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Видео:Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

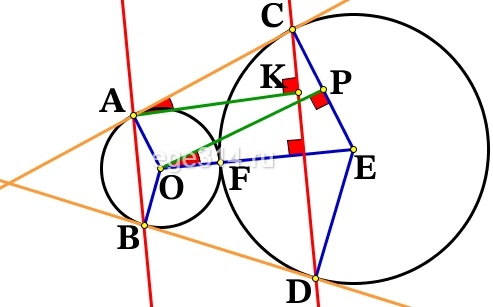
Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :

💥 Видео

две окружности касаются внешним образом в точке КСкачать

ОГЭ 2023 Ященко 4 вариант ФИПИ школе полный разбор!Скачать

Математика ЕГЭ-2024. Вариант 32 из сборника И.В. Ященко "36 вариантов заданий". Профильный уровень.Скачать

Разбор ОГЭ по математике 2023. Вариант 4 Ященко. Онлайн школа EXAMhackСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Разбор ОГЭ по математике 2023. Вариант 3 Ященко. Онлайн школа EXAMhackСкачать

Касающиеся внешним образом окружности и две общие касательные к нимСкачать