Окружности радиусов 22 и 99 точки а и в

Геометрия | 5 — 9 классы

26 Окружности радиусов 22 и 99 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и В — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Касательные АС и ВД образуют угол, биссектриса которого проходит через центры окружностей О1О2.

Половина этого углаα равна углу между радиусами R1и R2, проведенными в точку касания и прямыми АВ и СД.

Проведём отрезок из точки касания меньшей окружностипараллельно О1О2 до прямой СД.

Sinα = (R2 — R1) / (R2 + R1) = (99 — 22) / (99 + 22) = 7 / 11≈0, 636364.

Расстояние от середины АВ до R1 равно 22 * (7 / 11) = 14.

Расстояние от середины СД до R2 равно 99 * (7 / 11) = 63.

Ответ : расстояние между прямыми АВ и CD равно (22 + 99) + 14 — 63 = 72.

Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Под прямым углом из точки А к окружности проведены две касательные ?

Под прямым углом из точки А к окружности проведены две касательные .

Расстояние от точки А до цента окружности равно 2 см.

Найдите длину окружности.

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Нужен чертеж?

Решение не обязательно.

Окружности ω1 и ω2 с центрами O1 и O2 соответственно касаются внешним

L – их общая внешняя касательная.

Окружность ω касается ω1 и ω2,

а также прямой l в точке A.

Найдите площадь треугольника AO1O2, если

радиус ω1 равен 4, а радиус ω2 равен 9.

Видео:ОГЭ по математике. 9 класс. Задача 26. Вариант 5.Скачать

Окружности радиусов 12 и 20 касаются внешним образом?

Окружности радиусов 12 и 20 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и D — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Видео:16 задание ОГЭ математика 2023 | УмскулСкачать

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Из точки А проведены две касательные к окружности с центром в точке О?

Из точки А проведены две касательные к окружности с центром в точке О.

Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C?

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C.

Прямая AB касается окружности меньшего радиуса в точке A, а другой — точке B.

Через точку C проведена касательная, которая пересекает прямую AB в точке D.

А) Докажите, что вокруг четырёхугольника AOCD можно описать окружность

б) Найдите радиус этой окружности.

Видео:22 урок. ОГЭ | Окружности (практика) - часть 1Скачать

Окружности радиусов 45 и 90 касаются внешним образом?

Окружности радиусов 45 и 90 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D на второй .

При этом AC и BD – общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Решите пожалуйста?

Две окружности разных радиусов касаются друг друга внешним образом.

Две их общие касательные, которые не проходят через точку касания окружностей, касаются окружности меньшего радиуса в точках A и B, а окружности большего радиуса — в точках C и D.

При этом точки A и C лежат на одной касательной, а B и D на другой касательной.

Найдите расстояние между прямыми AB и CD, если радиусы окружностей равны 1, 5 и 6.

Видео:ОГЭ 2022 Демоверсия. 16 заданиеСкачать

Справедливы ли данные суждения?

Справедливы ли данные суждения?

1. Если прямая касательная окружности, то она имеет две общие точки с окружностью.

Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

Прямая и окружность могут иметь только две общие точки.

Видео:Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

Расстояние между центрами двух окружностей касающихся внешним образом равно 40 дм?

Расстояние между центрами двух окружностей касающихся внешним образом равно 40 дм.

Найдите радиусы окружностей, если один из них в 4 раза больше второго.

Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А?

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.

Найдите расстояние от точки В до окружности, если длина касательной равна 12 см.

С рисунком, пожалуйста.

На этой странице находится ответ на вопрос 26 Окружности радиусов 22 и 99 касаются внешним образом?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Видео:Длина окружности. Математика 6 класс.Скачать

Окружности радиусов 22 и 99 касается внешним образом

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

26 Окружности радиусов 22 и 99 касаются внешним образом?

Геометрия | 5 — 9 классы

26 Окружности радиусов 22 и 99 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и В — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Касательные АС и ВД образуют угол, биссектриса которого проходит через центры окружностей О1О2.

Половина этого углаα равна углу между радиусами R1и R2, проведенными в точку касания и прямыми АВ и СД.

Проведём отрезок из точки касания меньшей окружностипараллельно О1О2 до прямой СД.

Sinα = (R2 — R1) / (R2 + R1) = (99 — 22) / (99 + 22) = 7 / 11≈0, 636364.

Расстояние от середины АВ до R1 равно 22 * (7 / 11) = 14.

Расстояние от середины СД до R2 равно 99 * (7 / 11) = 63.

Ответ : расстояние между прямыми АВ и CD равно (22 + 99) + 14 — 63 = 72.

Видео:Разбор 3 варианта из сборника Ященко. Зонты | Математика ОГЭ 2023 | УмскулСкачать

Под прямым углом из точки А к окружности проведены две касательные ?

Под прямым углом из точки А к окружности проведены две касательные .

Расстояние от точки А до цента окружности равно 2 см.

Найдите длину окружности.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Нужен чертеж?

Решение не обязательно.

Окружности ω1 и ω2 с центрами O1 и O2 соответственно касаются внешним

L – их общая внешняя касательная.

Окружность ω касается ω1 и ω2,

а также прямой l в точке A.

Найдите площадь треугольника AO1O2, если

радиус ω1 равен 4, а радиус ω2 равен 9.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Окружности радиусов 12 и 20 касаются внешним образом?

Окружности радиусов 12 и 20 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и D — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:ОГЭ 2023 по математике. Геометрия. Окружность, свойства. Решение №16, 23, 24Скачать

Из точки А проведены две касательные к окружности с центром в точке О?

Из точки А проведены две касательные к окружности с центром в точке О.

Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.

Видео:Задание 26 из Варианта Ларина №230 обычная версия ОГЭ-2020.Скачать

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C?

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C.

Прямая AB касается окружности меньшего радиуса в точке A, а другой — точке B.

Через точку C проведена касательная, которая пересекает прямую AB в точке D.

А) Докажите, что вокруг четырёхугольника AOCD можно описать окружность

б) Найдите радиус этой окружности.

Окружности радиусов 45 и 90 касаются внешним образом?

Окружности радиусов 45 и 90 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D на второй .

При этом AC и BD – общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Решите пожалуйста?

Две окружности разных радиусов касаются друг друга внешним образом.

Две их общие касательные, которые не проходят через точку касания окружностей, касаются окружности меньшего радиуса в точках A и B, а окружности большего радиуса — в точках C и D.

При этом точки A и C лежат на одной касательной, а B и D на другой касательной.

Найдите расстояние между прямыми AB и CD, если радиусы окружностей равны 1, 5 и 6.

Справедливы ли данные суждения?

Справедливы ли данные суждения?

1. Если прямая касательная окружности, то она имеет две общие точки с окружностью.

Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

Прямая и окружность могут иметь только две общие точки.

Расстояние между центрами двух окружностей касающихся внешним образом равно 40 дм?

Расстояние между центрами двух окружностей касающихся внешним образом равно 40 дм.

Найдите радиусы окружностей, если один из них в 4 раза больше второго.

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А?

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.

Найдите расстояние от точки В до окружности, если длина касательной равна 12 см.

С рисунком, пожалуйста.

На этой странице находится ответ на вопрос 26 Окружности радиусов 22 и 99 касаются внешним образом?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Расстояние от точки пересечения диагоналей до большей стороны обозначим за х, соответственно 2х — это будет длина меньшей сторона прямоугольника. Из условия задачи расстояние от точки пересечения до меньшей стороны будет х + а, значит длина большей ..

Всё подробно написала в решении.

Формула : F = nr ^ 2 F = 80 кв. М n = 3, 14 r = ? — — — — — — — — — 80 = 3, 14 * r ^ 2 r ^ 2 = 80 : 3, 14 r ^ 2 ≈ 25, 48 r≈ 5, 048 Ответ : радиус≈ 5, 048м.

Площадь круга высчитывается по формуле s = n, n — это «пи». Введём известные данные : 80 = 3, 14 ; ; r = .

R = 19 a = 2R = 38 S = a(В квадрате) = 36(В квадрате) = 1296. Вроде так.

1. Угол K 2. Сторона NK.

А это правильно если это правильно спасибо большое.

Предположим, , что условие задачи такое : Отрезок МК, равный 35см, разделен точкой Р на два отрезка, причем отрезок МР в 6 раз больше отрезка КР. Найти длину отрезка КР. Решение : если КР = х, то МР = 6х и в сумме они равны 7х = 35см. Тогда х = 5с..

1. Найдём чистое время, которое теплоход находится в пути туда и обратно : 14 — 8 — 1 = 5 часов 2. Обозначим расстояние между городами за х. Время которое теплоход тратит на путь, когда он плывет по течению : х / (20 + 4) = х / 24 Время, которое те..

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

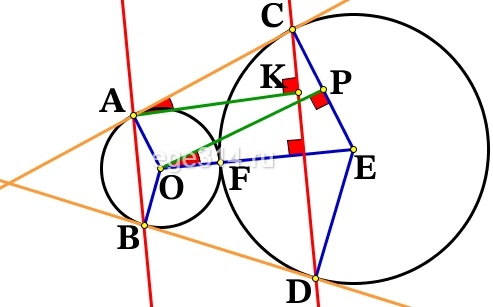
Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :