Видео:Задание 16 из реального ЕГЭ по математикеСкачать
Ваш ответ
Видео:Геометрия Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хордыСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,937
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать
Окружность высекает на сторонах четырехугольника равные хорды
Задание 16. Окружность с центром в точке О пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону АВ в точках K и L так, что АК = 13, KL = 6, LB = 1.
а) ABCD – трапеция, BL – биссектриса, следовательно, 
. Так как AD параллельна BC, то 
и 
, следовательно, угол ALB=90° и BL перпендикуляра AC.
Аналогично доказывается, что CL перпендикулярна BD. Получаем, что диагонали BD и AC перпендикулярны и в то же время являются биссектрисами углов. Следовательно, трапеция ABCD – это ромб, а у ромба биссектрисы всех углов пересекаются в одной точке.
б) Задача сводится к нахождению высоты ромба. Рассмотрим равнобедренный треугольник OLK, т.к. OL=OK как радиусы одной окружности.
Далее, 
, следовательно, OH – медиана и LH=KH:
Так как OH – высота прямоугольного треугольника OAB, то
Видео:#58. Олимпиадная задача о четырехугольникеСкачать
Равные хорды
Выясним, какими свойствами обладают равные хорды и равные дуги.
Равные хорды равноудалены от центра окружности.
Дано : окр. (O;R), AB и CD — хорды,
Соединим центр окружности с концами хорд.
I. Рассмотрим треугольники AOB и COD.
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.
II. Рассмотрим прямоугольные треугольники AOF и COK.
2) ∠A=∠C (по доказанному).
Из равенства треугольников следует равенство соответствующих сторон: OF=OK.
Что и требовалось доказать .
Если хорды равноудалены от центра окружности, то они равны.
Дано: окр. (O;R), AB и CD — хорды,
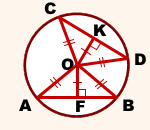
Соединим центр окружности с концами хорд.
I. Рассмотрим прямоугольные треугольники OKD и OFB.
1)OF=OK (по условию)
2)OD=OB (как радиусы).
Из равенства треугольников следует равенство соответствующих сторон:
II. Рассмотрим треугольники AOB и COD.
Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.
По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.
Что и требовалось доказать.
Равные хорды стягивают равные дуги.
Дано : окр. (O;R), AB и CD — хорды, AB=CD,
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.
Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD
Что и требовалось доказать .
Хорды, стягивающие равны дуги, равны.
Дано: окр. (O;R), AB и CD — хорды,
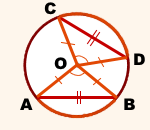
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.
Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.
Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
📺 Видео
Вписанные четырехугольники. 9 класс.Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Четырехугольники, вписанные в окружность. 9 класс.Скачать
3 правила для вписанного четырехугольника #shortsСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
ЕГЭ Задание 16 Первый признак подобия треугольниковСкачать
Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать
Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать
Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать
Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать
№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать
Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать
