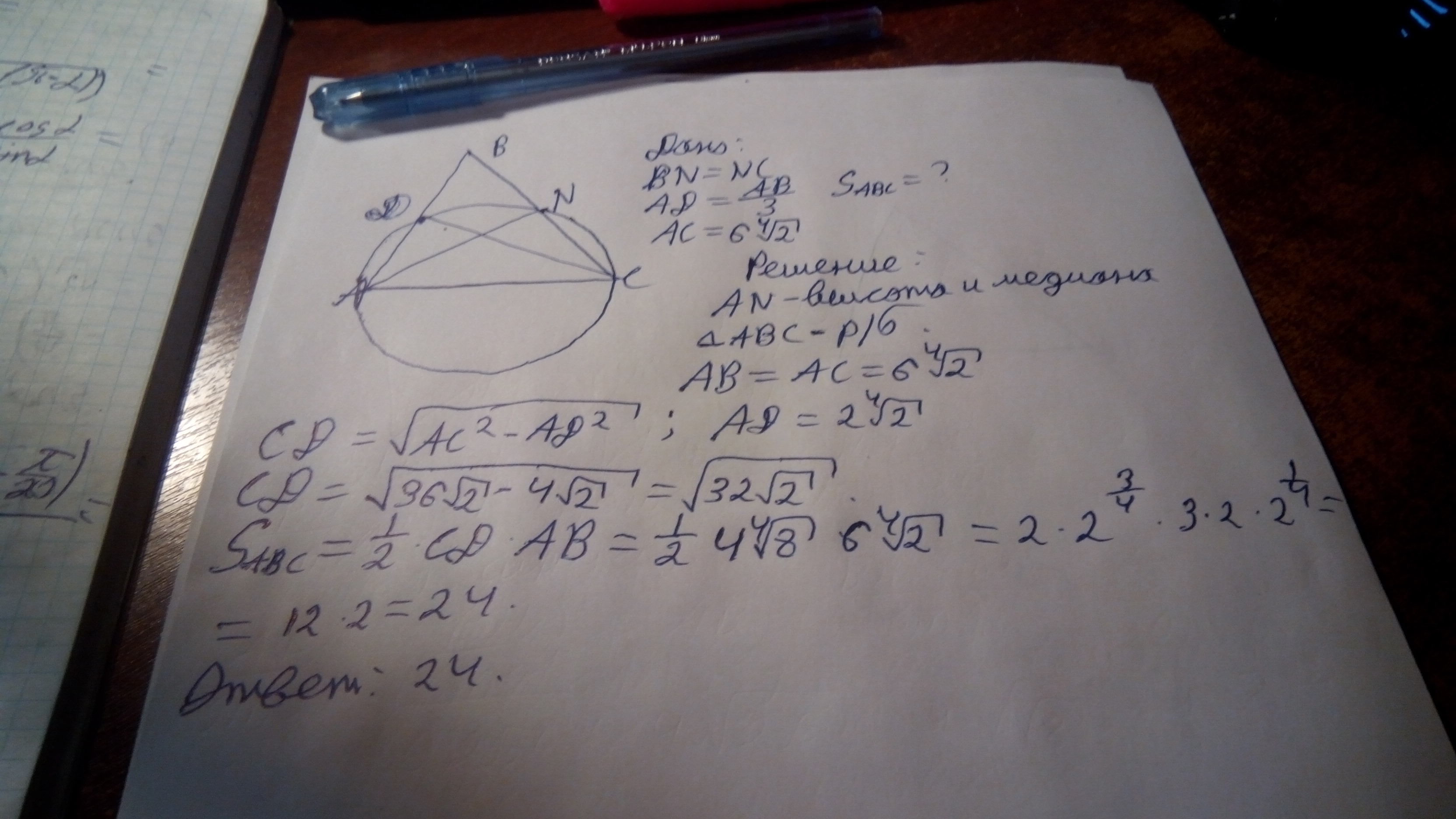Окружности построенные на сторонах ab и bc треугольника abc

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Видео:На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC Точка M — сереСкачать

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Видео:№28. На сторонах АВ и АС треугольника ABC взяты соответственноСкачать

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность, построенная на стороне AC треугольника ABC как на диаметре, проходит через середину стороны BC и пересекает сторону АВ в точке D так, что AD = AB / 3?

Геометрия | 5 — 9 классы

Окружность, построенная на стороне AC треугольника ABC как на диаметре, проходит через середину стороны BC и пересекает сторону АВ в точке D так, что AD = AB / 3.

Найдите площадь треугольника ABC, если AC = 6[tex] sqrt[4] [ / tex] .

Решение на фотографии.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

СРОЧНО?

Серединный перпендикуляр стороны AB треугольника ABC пересекает сторону BC в точке M.

Найдите длину стороны AC треугольника ABC, если BC = 16 см, а периметр треугольника AMC равен 26 см.

Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

Серединный перпендикуляр стороны AB треугольника ABC пересекает сторону в точке M найдите длину отрезка AC треугольника ABC если BC = 16см а периметр треугольника AMC = 26 см?

Серединный перпендикуляр стороны AB треугольника ABC пересекает сторону в точке M найдите длину отрезка AC треугольника ABC если BC = 16см а периметр треугольника AMC = 26 см.

Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

Чему равен радиус окружности, описанной около равностороннего треугольника со стороной [tex] sqrt[ / tex] помогите плииииз?

Чему равен радиус окружности, описанной около равностороннего треугольника со стороной [tex] sqrt[ / tex] помогите плииииз!

Видео:✓ Спидран: Красивая олимпиадная планиметрия за 5 минут | Осторожно, спойлер! | Борис ТрушинСкачать

На стороне AB треугольника ABC, как на диаметре, построена окружность ?

На стороне AB треугольника ABC, как на диаметре, построена окружность .

Она пересекает стороны AC и BC в точках M и N.

Как через точку С провести прямую перпендикулярную AB?

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Сторона правильного треугольника равна 2[tex] sqrt [ / tex] см?

Сторона правильного треугольника равна 2[tex] sqrt [ / tex] см.

Найдите радиус вписанной в треугольник окружности.

А) [tex] sqrt [ / tex] см.

В) 2 [tex] sqrt [ / tex] см.

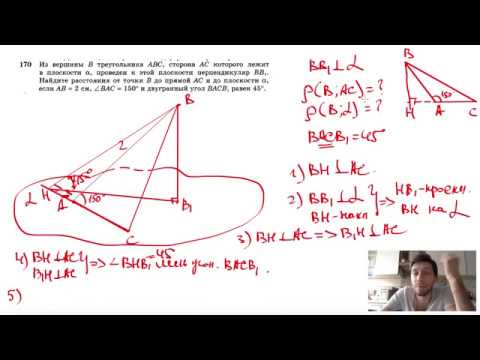
Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

На стороне ВС треугольника ABC взята точка D так, что [tex] frac [ / tex] = [tex] frac [ / tex]?

На стороне ВС треугольника ABC взята точка D так, что [tex] frac [ / tex] = [tex] frac [ / tex].

Докажите, что AD — биссектриса треугольника ABC.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Вычисли радиус окружности, описанной около равностороннего треугольника, если его сторона равна 9[tex] sqrt [ / tex]?

Вычисли радиус окружности, описанной около равностороннего треугольника, если его сторона равна 9[tex] sqrt [ / tex].

Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

В треугольнике ABC со сторонами AB = 12, BC = 15, AC = 9 проведена биссектриса [tex]BB_1[ / tex]?

В треугольнике ABC со сторонами AB = 12, BC = 15, AC = 9 проведена биссектриса [tex]BB_1[ / tex].

Пусть [tex]C_1[ / tex] — точка касания AB с вписанной в треугольник окружностью, отрезки [tex]BB_1[ / tex] и [tex]CC_1[ / tex] пересекаются в точке P, продолжение AP пересекает BC в точке [tex]A_1[ / tex].

Видео:ЕГЭ задание 16 Пять треугольниковСкачать

Найдите сторону правильного треугольника, если радиус вписанной в него окружности равен [tex] sqrt [ / tex]?

Найдите сторону правильного треугольника, если радиус вписанной в него окружности равен [tex] sqrt [ / tex].

Видео:Разбор Задачи №16 из Варианта Ларина №273Скачать

Найдите диаметр окружности, описанной ВОКРУГ правильного треугольника со стороной 7[tex] sqrt [ / tex]?

Найдите диаметр окружности, описанной ВОКРУГ правильного треугольника со стороной 7[tex] sqrt [ / tex].

Если вам необходимо получить ответ на вопрос Окружность, построенная на стороне AC треугольника ABC как на диаметре, проходит через середину стороны BC и пересекает сторону АВ в точке D так, что AD = AB / 3?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

1. задание : найти АС. Что это значит? ЭТО значит, что 6 см + 9 см = 15 см , так как АВ = 6 см , а ВС = 9 см, задание НАЙТИ АС. 2. ЗАДАНИЕ : найти МК всё точно также складываем 12см + 3 см = 15 см 3. Найти ошибку там ты написала правильно что 6, ..

Дано : AM = MN = NB и МК||NP||BC. Проведем МЕ и ND параллельно АС. Теорема ФалесаЕсли на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второ..

24 — 8 = 16см — это ВС АС = 8см.

Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций ..

Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона.

Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8.

1) вектор а = 2i — j 2) координаты вектора c .

Вот, пожалуйста✩ ^ _ ^ Все очень просто решается по теореме Пифагора.

Решение задания приложено.

ВС = MB — MC = 18, 2 — 9, 4 = 8, 8 Ответ : 1.

Видео:Геометрия На сторонах AB, BC и AC треугольника ABC отметили соответственно точки M, K и D такСкачать

Окружности построенные на сторонах ab и bc треугольника abc

И.М. Смирнова, В.А. Смирнов

ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ И ЛИНИИ ТРЕУГОЛЬНИКА

В новых стандартах профильного уровня обучения для старших классов предусмотрено изучение раздела « Геометрия на плоскости», в который включены следующие вопросы.

Свойство биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей. Формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей.

Вычисление углов с вершиной внутри и вне круга, угла между хордой и касательной.

Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма

Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников.

Геометрические места точек.

Решение задач с помощью геометрических преобразований и геометрических мест.

Теорема Чевы и теорема Менелая.

Эллипс, гипербола, парабола как геометрические места точек.

Неразрешимость классических задач на построение.

Здесь мы рассмотрим свойства биссектрис, медиан и высот треугольника, расширим число замечательных точек и линий треугольника, сформулируем и докажем теоремы Чевы, Менелая, Ван-Обеля, Стюарта и др., решим ряд задач на применение этих теорем, предложим задачи для самостоятельного решения и укажем дополнительную литературу.

Представленный материал может быть использован как на основных уроках, так и при проведении элективных курсов, написании рефератов и проектов, подготовки школьников к турнирам, конкурсам и олимпиадам по математике.

Начнем с задач, относящихся к расположению биссектрис, медиан и высот треугольника. Их решение, с одной стороны, позволяет вспомнить пройденный ранее материал, а с другой стороны, развивает необходимые геометрические представления учащихся, подготавливает их к решению более сложных задач.

Задача 1. По углам A и B треугольника ABC ( Ð A Ð B ) определите угол между высотой и биссектрисой, проведенными из вершины C .

Решение. Пусть CD – высота, CE – биссектриса, тогда Ð BCD = 90 ° — Ð B , Ð BCE = (180 ° — Ð A — Ð B ):2. Следовательно, Ð DCE = .

Задача 2. К какой из вершин треугольника ближе расположена точка пересечения биссектрис?

Решение. Пусть O – точка пересечения биссектрис треугольника ABC (рис. 1) . Воспользуемся тем, что против большей стороны треугольника лежит больший угол. Если AB > BC , то Ð A Ð C и, следовательно, Ð OAD Ð OCD . Поэтому OC OA , т.е. центр O вписанной окружности лежит ближе к вершине, расположенной против большей стороны.

Задача 3. Какая из высот треугольника наименьшая?

Решение. Пусть O – точка пересечения высот треугольника ABC (рис. 2). Если AC AB , то Ð C > Ð B . Окружность с диаметром BC пройдет через точки F и G . Учитывая, что из двух хорд меньше та, на которую опирается меньший вписанный угол, получаем, что CG BF , т.е. меньше та высота, которая опущена на большую сторону.

Задача 4. Пусть в остроугольном треугольнике ABC (рис. 3) точки A ₁ , B ₁ , C ₁ обозначают основания высот. Докажите, что точка H пересечения высот треугольника ABC является точкой пересечения биссектрис треугольника A ₁ B ₁ C ₁ .

Доказательство. На сторонах AC и BC треугольника ABC , как на диаметрах, построим окружности. Точки A ₁ , B ₁ , C ₁ принадлежат этим окружностям. Поэтому Ð B ₁ C ₁ C = Ð B ₁ BC , как углы, опирающиеся на одну и ту же дугу окружности. Ð B ₁ BC = Ð CAA ₁ , как углы с взаимно перпендикулярными сторонами. Ð CAA ₁ = Ð CC ₁ A ₁ , как углы, опирающиеся на одну и ту же дугу окружности. Следовательно, Ð B ₁ C ₁ C = Ð CC ₁ A ₁ , т.е. CC ₁ является биссектрисой угла B ₁ C ₁ A ₁ . Аналогичным образом показывается, что AA ₁ и BB ₁ являются биссектрисами углов B ₁ A ₁ C ₁ и A ₁ B ₁ C ₁ .

Самостоятельно исследуйте случаи прямоугольного и тупоугольного треугольника.

Рассмотренный треугольник, вершинами которого являются основания высот данного остроугольного треугольника, дает ответ на одну из классических экстремальных задач.

Задача 5 (задача Фаньяно). В данный остроугольный треугольник вписать треугольник наименьшего периметра.

Решение. Пусть ABC – данный остроугольный треугольник. На его сторонах требуется найти такие точки A ₁ , B ₁ , C ₁ , для которых периметр треугольника A ₁ B ₁ C ₁ был бы наименьшим (рис. 4).

Зафиксируем сначала точку C ₁ и будем искать точки A ₁ и B ₁ , для которых периметр треугольника A ₁ B ₁ C ₁ наименьший (при данном положении точки C ₁ ).

Для этого рассмотрим точки D и E симметричные точке C ₁ относительно прямых AC и BC . Тогда B ₁ C ₁ = B ₁ D , A ₁ C ₁ = A ₁ E и, следовательно, периметр треугольника A ₁ B ₁ C ₁ будет равен длине ломаной DB ₁ A ₁ E . Ясно, что длина этой ломаной наименьшая, если точки B ₁ , A ₁ лежат на прямой DE .

Будем теперь менять положение точки C ₁ , и искать такое положение, при котором периметр соответствующего треугольника A ₁ B ₁ C ₁ наименьший.

Так как точка D симметрична C ₁ относительно AC , то CD = CC ₁ и ACD = ACC ₁ . Аналогично, CE = CC ₁ и BCE = BCC ₁ . Следовательно, треугольник CDE равнобедренный. Его боковая сторона равна CC ₁ . Основание DE равно периметру p треугольника A ₁ B ₁ C ₁ . Угол DCE равен удвоенному углу ACB треугольника ABC и, значит, не зависит от положения точки C ₁ .

В равнобедренном треугольнике с данным углом при вершине основание тем меньше, чем меньше боковая сторона. Поэтому наименьшее значение периметра p достигается в случае наименьшего значения CC ₁ . Это значение принимается в случае, если CC ₁ является высотой треугольника ABC . Таким образом, искомой точкой C ₁ на стороне AB является основание высоты, проведенной из вершины C .

Заметим, что мы могли бы фиксировать сначала не точку C ₁ , а точку A ₁ или точку B ₁ и получили бы, что A ₁ и B ₁ являются основаниями соответствующих высот треугольника ABC .

Из этого следует, что искомым треугольником, наименьшего периметра, вписанным в данный остроугольный треугольник ABC является треугольник, вершинами которого служат основания высот треугольника ABC .

Рассмотрим теперь замечательные точки и линии треугольника. К числу таких точек, изучаемых в школьном курсе геометрии, относятся:

а) точка пересечения биссектрис (центр вписанной окружности);

б) точка пересечения серединных перпендикуляров (центр описанной окружности);

в) точка пересечения высот (ортоцентр);

г) точка пересечения медиан (центроид).

Добавим к ним некоторые другие замечательные точки и линии.

Точка Торричелли. Путь дан треугольник ABC. Точкой Торричелли этого треугольника называется такая точка O, из которой стороны данного треугольника видны под углом 120 ° (рис. 5), т.е. углы AOB, AOC и BOC равны 120 ° .

Докажем, что в случае, если все углы треугольника меньше 120 ° , то точка Торричелли существует.

На стороне AB треугольника ABC построим равносторонний треугольник ABC ‘ (рис. 6, а), и опишем около него окружность. Отрезок AB стягивает дугу этой окружности величиной 120 ° . Следовательно, точки этой дуги, отличные от A и B , обладают тем свойством, что отрезок AB виден из них под углом 120 ° . Аналогичным образом, на стороне AC треугольника ABC построим равносторонний треугольник ACB ‘ (рис. 6, а), и опишем около него окружность. Точки соответствующей дуги, отличные A и C , обладают тем свойством, что отрезок AC виден из них под углом 120 ° . В случае, когда углы треугольника меньше 120 ° , эти дуги пересекаются в некоторой внутренней точке O . В этом случае Ð AOB = 120 ° , Ð AOC = 120 ° . Следовательно, и Ð BOC = 120 ° . Поэтому точка O является искомой.

В случае, когда один из углов треугольника, например ABC , равен 120 ° , точкой пересечения дуг окружностей будет точка B (рис. 6, б). В этом случае точки Торричелли не существует, так как нельзя говорить об углах, под которыми видны из этой точки стороны AB и BC .

В случае, когда один из углов треугольника, например ABC , больше 120 ° (рис. 6, в), соответствующие дуги окружностей не пересекаются, и точки Торричелли также не существует.

С точкой Торричелли связана задача Ферма о нахождении точки, сумма расстояний от которой до трех данных точек наименьшая.

Задача 6 (задача Ферма). Для данного треугольника найдите точку, сумма расстояний от которой до вершин треугольника принимает наименьшее значение.

Решение. Докажем, что в случае, если углы треугольника меньше 120 ° , то искомой точкой в задаче Штейнера является точка Торричелли.

Повернем треугольник ABC вокруг вершины C на угол 60 ° , рис. 7. Получим треугольник A ’ B ’ C . Возьмем произвольную точку O в треугольнике ABC . При повороте она перейдет в какую-то точку O ’ . Треугольник OO ’ C равносторонний, так как CO = CO ’ и Ð OCO ’ = 60 ° , следовательно, OC = OO ’ . Поэтому сумма длин O A + OB + OC будет равна длине ломаной A O + OO ’ + O ’ B ’ . Ясно, что наименьшее значение длина этой ломаной принимает в случае, если точки A , O , O ’ , B ’ лежат на одной прямой. Если O – точка Торричелли, то это так. Действительно, Ð AOC = 120 ° , Ð COO’ = 60 ° . Следовательно, точки A , O , O ’ лежат на одной прямой. Аналогично, Ð CO ’ O = 60 ° , Ð CO’B’ = 120 ° . Следовательно, точки O , O ’ , B ’ лежат на одной прямой. Значит, все точки A , O , O ’ , B ’ лежат на одной прямой.

Самостоятельно докажите, что в случае, если один из углов треугольника больше или равен 120 ° , то решением задачи Ферма является вершина этого угла.

Окружность девяти точек. Пусть в треугольнике ABC (рис. 8), H – точка пересечения высот треугольника; точки A₁, B₁, C₁ обозначают основания высот; A₂, B₂, C₂ – середины соответствующих сторон; A₃, B₃, C₃ – середины отрезков AA₁, BB₁ и CC₁. Тогда точки A₁, B₁, C₁, A₂, B₂, C₂, A₃, B₃, C₃ лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера.

Действительно, A ₃ B ₂ – средняя линия треугольника AHC и, следовательно, A ₃ B ₂ || CC ₁ . B ₂ A ₂ – средняя линия треугольника ABC и, следовательно, B ₂ A ₂ || AB . Так как CC ₁ ^ AB , то A ₃ B ₂ A ₂ = 90 ° . Аналогично, A ₃ C ₂ A ₂ = 90 ° . Поэтому точки A ₂ , B ₂ , C ₂ , A ₃ лежат на одной окружности с диаметром A ₂ A ₃ . Так как AA ₁ ^ BC , то точка A ₁ также принадлежит этой окружности. Таким образом, точки A ₁ и A ₃ лежат на окружности, описанной около треугольника A ₂ B ₂ C ₂ . Аналогичным образом показывается, что точки B ₁ и B ₃ , C ₁ и C ₃ лежат на этой окружности. Значит, все девять точек лежат на одной окружности.

Прямая Эйлера. В треугольнике центр описанной окружности, точка пересечения медиан, точка пересечения высот и центр окружности девяти точек лежат на одной прямой, называемой прямой Эйлера. При этом центр окружности девяти точек лежит посередине между центром пересечения высот и центром описанной окружности.

Действительно, пусть в треугольнике ABC (рис. 9), точка O – центр описанной окружности; G – точка пересечения медиан. H точка пересечения высот . Требуется доказать, что точки O , G , H лежат на одной прямой и центр окружности девяти точек N делит отрезок OH пополам.

Рассмотрим гомотетию с центром в точке G и коэффициентом -0,5. Вершины A , B , C треугольника ABC перейдут, соответственно в точки A ₂ , B ₂ , C ₂ . Высоты треугольника ABC перейдут в высоты треугольника A ₂ B ₂ C ₂ и, следовательно, точка H перейдет в точку O . Поэтому точки O , G , H будут лежать на одной прямой.

Покажем, что середина N отрезка OH является центром окружности девяти точек. Действительно, C ₁ C ₂ – хорда окружности девяти точек. Поэтому серединный перпендикуляр к этой хорде является диаметром и пересекает OH в середине N . Аналогично, серединный перпендикуляр к хорде B ₁ B ₂ является диаметром и пересекает OH в той же точке N . Значит N – центр окружности девяти точек. Что и требовалось доказать.

Прямая Симсона. Для произвольного треугольника основания перпендикуляров, опущенных из любой точки описанной около него окружности на его стороны или их продолжения, лежат на одной прямой, называемой прямой Симсона.

Действительно, пусть P – произвольная точка, лежащая на окружности, описанной около треугольника ABC ; D , E , F – основания перпендикуляров, опущенных из точки P на стороны треугольника (рис. 10). Покажем, что точки D , E , F лежат на одной прямой.

Заметим, что в случае, если AP проходит через центр окружности, то точки D и E совпадают с вершинами B и C . В противном случае, один из углов ABP или ACP острый, а другой – тупой. Из этого следует, что точки D и E будут расположены по разные стороны от прямой BC и для того, чтобы доказать, что точки D , E и F лежат на одной прямой, достаточно проверить, что Ð C EF = Ð BED .

Опишем окружность с диаметром CP . Так как Ð CFP = Ð CEP = 90 ° , то точки E и F лежат на этой окружности. Поэтому Ð C EF = Ð CPF как вписанные углы, опирающиеся на одну дугу окружности. Далее, Ð CPF = 90 ° — Ð PCF = 90 ° — Ð DBP = Ð BPD . Опишем окружность с диаметром BP . Так как Ð BEP = Ð BDP = 90 ° , то точки F и D лежат на этой окружности. Поэтому Ð BPD = Ð BED . Следовательно, окончательно получаем, что Ð C EF = Ð BED . Значит точки D , E , F лежат на одной прямой.

Задачи для самостоятельного решения

1. По углам A и B прямоугольного треугольника ABC ( Ð A Ð B ) определите угол между высотой и медианой, проведенными из вершины C прямого угла.

2. Может ли точка пересечения биссектрис треугольника находится вне этого треугольника?

3. Может ли точка пересечения медиан треугольника находиться вне этого треугольника?

4. Может ли точка пересечения высот или их продолжений находится вне этого треугольника?

5. Где находится точка пересечения серединных перпендикуляров к сторонам: а) прямоугольного треугольника; б) остроугольного треугольника; в) тупоугольного треугольника?

Ответ: а) в середине гипотенузы; б) внутри треугольника; в) вне треугольника.

6. К какой из вершин треугольника ближе расположен ортоцентр?

Ответ: К вершине большего угла.

7. К какой из сторон треугольника ближе расположен ортоцентр?

Ответ: К меньшей.

8. К какой из сторон треугольника ближе расположена точка пересечения медиан?

Ответ: К большей.

9. Может ли одна биссектриса треугольника проходить через середину другой?

10. Углы В и С треугольника АВС равны соответственно 10 ° и 100 ° . Найдите углы ВОС и СОА, где О — центр описанной окружности.

Ответ: 140 ° и 20 ° .

11. Докажите, что из четырех точек, одна из которых есть ортоцентр треугольника, с вершинами в трех остальных точках, каждая является центроидом треугольника с вершинами в трех остальных точках.

12. Пусть АВС D — параллелограмм. Докажите, что точки пересечения медиан треугольников АВС и DCA лежат на диагонали BD и делят ее на три равные части.

13. Разделите данный отрезок на три равные части, не пользуясь построением параллельных прямых.

14. Пусть Н — точка пересечения высот треугольника АВС. Докажите, что радиусы окружностей, описанных около треугольников АВС, АНВ, ВНС, СНА равны между собой.

15. Докажите, что если какие-нибудь из замечательных точек треу­гольника совпадают, то этот треугольник — равносторонний.

Рассмотрим теперь теоремы, позволяющие устанавливать, в каком случае три точки, лежащие на сторонах треугольника или их продолжениях, принадлежат одной прямой (теорема Менелая), а также, в каком случае три прямые, проходящие через вершины треугольника и противоположные им стороны треугольника, пересекаются в одной точке (теорема Чевы).

Начнем с теоремы Менелая, доказанной древнегреческим математиком и астрономом Менелаем Александрийским, жившим в I веке до нашей эры.

Теорема (Менелая). Пусть на сторонах AB , BC и продолжении стороны AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ . Точки A ₁ , B ₁ , C ₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство

(*)

Доказательство. Предположим, что точки A ₁ , B ₁ , C ₁ принадлежат одной прямой a (рис. 11). Через вершину C треугольника ABC проведем прямую, параллельную a и обозначим через D точку ее пересечения с AB . Из подобия треугольников ADC и AC ₁ B следует выполнимость равенства

(1)

Аналогично, из подобия треугольников BDC и BC ₁ A ₁ следует выполнимость равенства

(2)

Перемножая эти равенства, получим равенство

из которого следует требуемое равенство (*)

Докажем обратное. Пусть на сторонах AB , BC и продолжении стороны AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ , для которых выполняется равенство (*). Предположим, что прямая A ₁ B ₁ пересекает прямую AB в некоторой точке C ‘ . По доказанному, выполняется равенство

Учитывая равенство (*), получаем равенство из которого следует совпадение точек C ‘ и C ₁ и, значит, точки A ₁ , B ₁ , C ₁ принадлежат одной прямой.

Предложим еще один способ доказательства теоремы Менелая.

Пусть точки A ₁ , B ₁ , C ₁ принадлежат одной прямой a (рис. 12). Опустим из вершин треугольника ABC перпендикуляры AA ’ , BB ’ , CC ’ на эту прямую.

Аналогичным образом показывается, что

и

Перемножая полученные равенства, будем иметь

Задача 7 . Точка C ₁ делит сторону AB треугольника ABC в отношении 2:1. Точка B ₁ лежит на продолжении стороны AC и AC = CB ₁ . В каком отношении делит прямая B ₁ C ₁ сторону BC ?

Решение. По условию, Используя теорему Менелая, находим

Задача 8. Используя теорему Менелая, доказать, что отрезки, соединяющие вершины тетраэдра с центроидами противоположных граней, пересекаются в одной точке, называемой центроидом тетраэдра, и делятся в ней в отношении 3:1, считая от вершин.

Доказательство. Действительно, пусть ABCD – тетраэдр, A ₂ , D ₂ – центроиды соответствующих граней, A ₁ – середина BC , O – точка пересечения AA ₂ и DD ₂ (рис. 13). Применим теорему Менелая к треугольнику A ₁ DD ₂ и прямой AA ₂ . Имеем

Так как A ₂ – точка пересечения медиан треугольника BCD , то Так как D ₂ – точка пересечения медиан треугольника ABC , то Поэтому

Заметим, что в таком же отношении делят отрезок DD ₂ прямые BB ₂ и CC ₂ . Следовательно, они также проходят через точку O и делятся в ней в отношении 3:1, считая от вершин.

Рассмотрим теперь теорему, опубликованную в 1678 году итальянским математиком и инженером Джованни Чевой.

Теорема (Чевы). Пусть на сторонах AB , BC и AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ . Прямые AA ₁ , BB ₁ , CC ₁ пересекаются в одной точке тогда и только тогда, когда

(*)

Доказательство. Предположим, что прямые AA ₁ , BB ₁ , CC ₁ пересекаются в точке O (рис. 14) . Через вершину C треугольника ABC проведем прямую, параллельную AB , и ее точки пересечения с прямыми AA ₁ , BB ₁ обозначим соответственно A ₂ , B ₂ . Из подобия треугольников CB ₂ B ₁ и ABB ₁ имеем равенство

(1)

Аналогично, подобия треугольников BAA ₁ и CA ₂ A ₁ имеем равенство

(2)

Далее, из подобия треугольников BC ₁ O и B ₂ CO , AC ₁ O и A ₂ CO имеем Следовательно, имеет место равенство

(3)

Перемножая равенства (1), (2) и (3), получим требуемое равенство (*).

Докажем обратное. Пусть для точек A ₁ , B ₁ , C ₁ , взятых на соответствующих сторонах треугольника ABC выполняется равенство (*). Обозначим точку пересечения прямых AA ₁ и BB ₁ через O и точку пересечения прямых CO и AB через C ‘ . Тогда, на основании доказанного, имеет место равенство

Учитывая равенство (*), получим равенство из которого следует совпадение точек C ‘ и C ₁ и, значит, прямые AA ₁ , BB ₁ , CC ₁ пересекаются в одной точке.

Предложим еще один способ доказательства теоремы Чевы, использующий понятие площади.

Предположим, что прямые AA ₁ , BB ₁ , CC ₁ пересекаются в точке O (рис. 15) . Опустим из вершин A и B треугольника ABC перпендикуляры AA ’ , BB ’ на прямую CC ₁ . Треугольники AC ₁ A ’ и BC ₁ B ’ подобны и, следовательно,

Аналогичным образом показывается, что

и

Перемножая полученные равенства, будем иметь

Заметим, что из теоремы Чевы непосредственно следует, что медианы треугольника пересекаются в одной точке.

Задача 9 . Используя теорему Чевы, доказать, что биссектрисы треугольника пересекаются в одной точке.

Доказательство. Пусть AA ’ , BB ’ , CC ’ – биссектрисы треугольника ABC . Тогда

Следовательно, и, значит, AA ’ , BB ’ , CC ’ пересекаются в одной точке.

Задача 10 . Точки C ₁ и A ₁ делят стороны AB и BC треугольника ABC в отношении 1:2. Прямые CC ₁ и AA ₁ пересекаются в точке O . Найдите отношение, в котором прямая BO делит сторону AC .

Решение. По условию, Используя теорему Чевы, имеем

Воспользуемся теоремой Чевы для установления еще одной замечательной точки треугольника.

Точка Жергона. Прямые, проходящие через вершины треугольника и точки касания вписанной окружности пересекаются в одной точке, называемой точкой Жергона.

Действительно, пусть окружность касается сторон треугольника ABC соответственно в точках A ₁ , B₁, C₁ (рис. 16). Тогда AB₁ = AC₁, BC₁ = BA₁, CA₁ = CB₁. Следовательно, и, значит, прямые AA₁, BB₁, CC₁ пересекаются в одной точке.

Теорема Ван-Обеля. Пусть на сторонах AB , BC и AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ . Если прямые AA ₁ , BB ₁ , CC ₁ пересекаются в точке O , то имеет место равенство

Доказательство. Через вершину C треугольника ABC проведем прямую, параллельную AB (рис. 17). Продолжим AA ₁ и BB ₁ до пересечения с этой прямой в точках A ’ и B ’ соответственно. Из подобия треугольников AOB и A ’ OB ’ имеем

Следовательно,

Из доказанной теоремы непосредственно следует, что медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.

Задача 1 1 . В каком отношении делятся биссектрисы треугольника точкой их пересечения.

Поэтому

Доказательство. Пусть С E – высота треугольника ABC (рис. 18). По теореме косинусов, примененной к треугольникам ADC и BDC , имеем

Умножим первое равенство на c ” , второе – на c ’ и сложим. Получим b 2 c ” + a 2 c ’ = ( c ’+ c ” ) c ’ c ” + d 2 ( c ’+ c ” ), из которого и следует требуемое равенство.

Задача 12. Используя теорему Стюарта, вычислить биссектрису CC ₁ = треугольника по его сторонам AB = c , AC = b , BC = a .

Решение. Воспользуемся тем, что биссектриса делит сторону треугольника на части, пропорциональные прилежащим сторонам. Обозначим AC ₁ = c ’ , BC ₁ = c ” . Тогда c ’ + c ” = c и ac ’ = bc ” . Из этих двух уравнений находим c ’ и c ” .

, .

Подставляя теперь эти выражения в равенство теоремы Стюарта, получим ( ) 2 c = a 2 + b 2 — c . Откуда

Задачи для самостоятельного решения

1. На продолжениях сторон AB , BC и CA треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ так, что AB = BC ₁ , BC = CA ₁ , CA = AB ₁ . Найдите отношение, в котором прямая AB ₁ делит сторону A ₁ C ₁ треугольника A ₁ B ₁ C ₁ .

2. Точки A ₁ и B ₁ делят стороны BC и AC треугольника ABC в отношениях 2:1 и 1:2. Прямые AA ₁ и BB ₁ пересекаются в точке O . Площадь треугольника ABC равна 1. Найдите площадь треугольника OBC .

3. На медиане CC ₁ треугольника ABC взята точка M . Прямые AM и BM пересекают стороны треугольника соответственно в точках A ₁ и B ₁ . Докажите, что прямые AB и A ₁ B ₁ параллельны.

4. Отрезок MN , соединяющий середины сторон AD и BC четырехугольника ABCD , делится диагоналями на три равные части. Докажите, что ABCD – трапеция, одно из оснований AB или CD которой вдвое больше другого.

5. Пусть на продолжении сторон AB , BC и AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ . Докажите, что точки A ₁ , B ₁ , C ₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство

6. Пусть на стороне AB и продолжении сторон BC и AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ . Докажите, что прямые A A ₁ , B B ₁ , C C ₁ пересекаются в одной точке, или параллельны тогда и только тогда, когда выполняется равенство

7. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке.

8. Д окажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон.)

9. Пусть на сторонах AB , BC и AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ так, что прямые AA ₁ , BB ₁ , CC ₁ пересекаются в точке O . Докажите, что выполняется равенство

10. Пусть на сторонах AB , BC и AC треугольника ABC взяты соответственно точки C ₁ , A ₁ и B ₁ так, что прямые AA ₁ , BB ₁ , CC ₁ пересекаются в точке O . Докажите, что выполняется равенство

11. Пусть на ребрах AB , BC , CD и AD тетраэдра ABCD взяты соответственно точки A ₁ , B ₁ , C ₁ и D ₁ . Докажите, что точки A ₁ , B ₁ , C ₁ , D ₁ лежат на одной плоскости тогда и только тогда, когда выполняется равенство

1. Адамар Ж. Элементарная геометрия, ч. I , Планиметрия. –М.: Учпедгиз, 1936

2. Ефремов Д. Новая геометрия треугольника. Одесса, 1902.

3. Зетель С.И. Новая геометрия треугольника. –М.: Учпедгиз, 1962.

4. Коксетер Г.С.М. Введение в геометрию. –М.: Наука, 1966.

5. Коксетер Г.С.М., Грейтцер С.Л. Новые встречи с геометрией. –М.: Наука, 1978.

6. Перепелкин Д.И. Курс элементарной геометрии, ч. I , Геометрия на плоскости. –М.: Учпедгиз, 1949.

7. Понарин Я.П. Элементарная геометрия, т. 1. –М.: МЦНМО, 2004.

🎬 Видео

Геометрия На сторонах AB и AC треугольника ABC отметили соответственно D и E так, что AD:DB = AE:ECСкачать

Геометрия Окружность, построена на стороне AB треугольника ABC как на диаметре, пересекает стороныСкачать

№164. На сторонах равностороннего треугольника ABC отложены равные отрезки AD, BE и CF, как показаноСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

На катете ML прямоугольного треугольника KLM как на диаметре построена окружностьСкачать

✓ Планиметрия от ЕГЭ до Всероса | #ТрушинLive #032 | Борис ТрушинСкачать