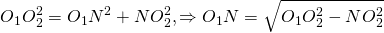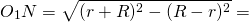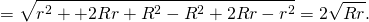Окружности касаются внешним образом найти расстояние между прямыми (2 видео)

Окружности касаются внешним образом

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

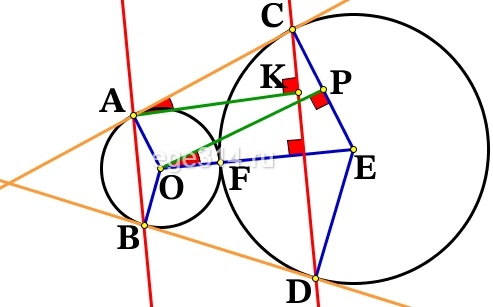
Соединим центры окружностей — точки O₁ и O₂ — с точками A и C соответственно.

Обозначим O₁A=r, O₂C=R.

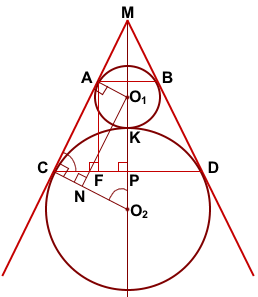
Проведём перпендикуляр AF к прямой CD и перпендикуляр O₁N к прямой CO₂.

AF — искомое расстояние между прямыми AB и CD.

Четырёхугольник AO₁NC — прямоугольник (так как у него три угла прямые).

Рассмотрим прямоугольный треугольник O₁O₂N.

Продлим касательные AC и BD до пересечения в точке M. Проведём луч MO₂.

Окружности с центрами в точках O₁ и O₂ вписаны в угол CMD, значит MP — биссектриса угла CMD.

MC=MD (как отрезки касательных, проведённых из одной точки). Значит треугольник CMD — равнобедренный с основанием CD. Следовательно, биссектриса MP является также его высотой.

В прямоугольном треугольнике CMP ∠MCP=90°-∠CMP.

В прямоугольном треугольнике CMO₂ ∠CO₂M=90°-∠CMP.

Отсюда ∠MCP=∠CO₂M. Следовательно, прямоугольные треугольники AFC и O₁NO₂ подобны (по острому углу).

Содержание

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …
Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?
Окружности радиусов 12 и 20 касаются внешним образом?
Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C?
Окружности радиусов 45 и 90 касаются внешним образом?
Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К?
Решите пожалуйста?
Справедливы ли данные суждения?
О₁ и О₂ — центры двух касающихся внешнем образом окружностей?
Прямая АВ касается окружности с центром О и радиусом 5 см в точке А?
Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью?
Окружности с радиусами, равными 4 см и 1 см, внутренне касаются?
🎦 Видео

Видео:ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :

Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?

Геометрия | 5 — 9 классы

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Расстояние между центрами О1 и О2 окружностей равно 36 + 45 = 81.

Из центра меньшей окружности проведём отрезок параллельно касательной до радиуса в точку касания большей окружности.

Синус угла между этим отрезком и линией О1О2 равен(45 — 36) / 81 = 9 / 81 = 1 / 9.

Этот угол равен углам между АВ и СД и радиусами в точки касания.

Тогда искомое расстояние L между АВ и СД равно :

L = 81 — 45 * (1 / 9) + 36 * (1 / 9) = 81 — 5 + 4 = 80.

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Окружности радиусов 12 и 20 касаются внешним образом?

Окружности радиусов 12 и 20 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и D — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Видео:Три окружности касаются прямой и друг друга внешним образомСкачать

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C?

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C.

Прямая AB касается окружности меньшего радиуса в точке A, а другой — точке B.

Через точку C проведена касательная, которая пересекает прямую AB в точке D.

А) Докажите, что вокруг четырёхугольника AOCD можно описать окружность

б) Найдите радиус этой окружности.

Видео:Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

Окружности радиусов 45 и 90 касаются внешним образом?

Окружности радиусов 45 и 90 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D на второй .

При этом AC и BD – общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:ОГЭ по математике. 9 класс. Задача 26. Вариант 5.Скачать

Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К?

Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К.

Найдите расстояние от точки А до ближайшей к ней точки окружности, если АК = 4.

Видео:Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

Решите пожалуйста?

Две окружности разных радиусов касаются друг друга внешним образом.

Две их общие касательные, которые не проходят через точку касания окружностей, касаются окружности меньшего радиуса в точках A и B, а окружности большего радиуса — в точках C и D.

При этом точки A и C лежат на одной касательной, а B и D на другой касательной.

Найдите расстояние между прямыми AB и CD, если радиусы окружностей равны 1, 5 и 6.

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Справедливы ли данные суждения?

1. Если прямая касательная окружности, то она имеет две общие точки с окружностью.

Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

Прямая и окружность могут иметь только две общие точки.

Видео:Расстояние между прямыми. Задание 14 (40)Скачать

О₁ и О₂ — центры двух касающихся внешнем образом окружностей?

О₁ и О₂ — центры двух касающихся внешнем образом окружностей.

Прямая О₁О₂ пересекает первую окружность (с центром в точке О₁) в точке А.

Определите диаметр второй окружности, если радиус первой равен 5 см, а касательная, проведенная из точки А ко второй окружности, образует с прямой О₁О₂ угол в 30ᵒ.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А?

Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.

Найдите расстояние от точки В до окружности, если длина касательной равна 12 см.

С рисунком, пожалуйста.

Видео:Расстояние между скрещивающимися прямымиСкачать

Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью?

Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью.

Построить окружность, которая касается прямой l и касается окружности в точке А.

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Окружности с радиусами, равными 4 см и 1 см, внутренне касаются?

Окружности с радиусами, равными 4 см и 1 см, внутренне касаются.

Хорда АВ большей окружности касается меньшей окружности, и прямая АВ образует с общей касательной в окружности угол 60°.

Вы зашли на страницу вопроса Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Надеюсь что понятно.

R = a / корень из 2 — формула нахождения радиуса описанной окружности. А — сторона квадрата R = 8 * корень из 2 / корень из 2 = 8 (сокращаем корни).

А)Около четырехугольника можно описать окружность, если суммы углов равны 180°. По теореме косинусов из треугольника АВС : АC2 = AB2 + CB2–2·AB·CB·cos∠B 49 = 9 + 25–30·cos∠B cos∠B = 15 / (–30) = –1 / 2 По теореме косинусов из треугольника АDС : АC2 ..

Решение : A = B 180 — (56 + 56) = 68.

Квадратный корень из 3 * 3 + 5 * 5 9 + 25 = 34 корень из 34 (клеток).

S = (8×11) / 2 = 44 Площадь равна полупроизведению двух катетов.

Трапеция прямоугольная, Углы А и В по 90 градДиагональ ВД является основанием равнобедренного тре — ка ВДС (по усл)Углы при основании будут равныПоскольку в трап основания параллельны, то диагональ ВД — секущая, углы СВД и ВДА противолежащие и равные..

АВС — рівнобедрений трикутник, у якого АВ = ВС = 50 ; ВК⊥АС. За умовою ВК = х ; АС = 1, 5х ; АК = 0, 75х. ΔАВК. АК² + ВК² = АВ² ; (0, 75х)² + х² = 2500 ; х² = 1600 ; х = 40 ; ВК = 40 см ; АС = 1, 5·40 = 60 см. S(АВС) = 0, 5ВК·АС = 0, 5·40·60 = 12..

В четырехугольнике ABCD диагонали пересекаются в точке О. DO = BO, DM — медиана треугольника ADO, BN — медиана треугольника CBO ; MO = NO. Доказать, что треугольник AMD = треугольнику CNB * * * В ∆ ВОN и ∆ MOD стороны МО = ОN ; ВО = ОD (дано), ∠ВОN..

ВЕ — биссектриса угла АВD ромба ( дано на рисунке). Угол ВЕD = 150° Примем угол DBE равным х. Угол ВDЕ = ∠ABD, поэтому угол ВDE = 2х В треугольнике ВЕD сумма∠ВЕD + ∠DBE + EDB = 180° 150° + х + 2х = 180°⇒ 3х = 30 х = 10 Диагонали ромба являются бисс..