Окружность вписанная в треугольник abc касается стороны ab

Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать

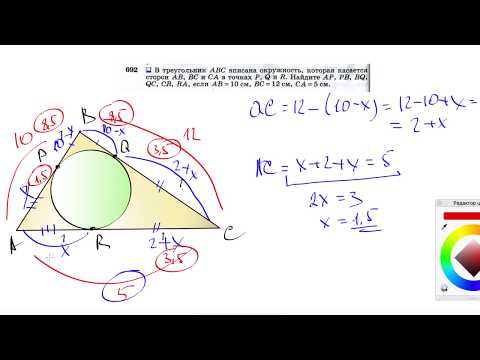
Ваш ответ

Видео:Геометрия Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. НайдитеСкачать

решение вопроса

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,997
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать

Окружность вписанная в треугольник abc касается стороны ab

Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB и AC соответственно. Прямые MN и EF пересекаются в точке D.

а) Докажите, что треугольник DFN равнобедренный.

б) Найдите площадь треугольника BED, если AB = 28 и ∠ABC = 60°.

а) Поскольку CM = CN, треугольник MCN равнобедренный. Прямые EF и BC параллельны, поэтому треугольник DFN подобен треугольнику MCN, следовательно, треугольник DFN также равнобедренный: DF = NF.

б) Обозначим BC = a, AC = b, AB = c. Пусть p — полупериметр треугольника ABC. Предположим, что a > c. Тогда

Значит, то есть треугольник BED равнобедренный.

Аналогично для a ≤ c.

Поскольку прямые ED и BC параллельны,

Следовательно,

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен , то угол KLM равен Пусть Р – центр вписанной окружности треугольника АВС. В четырехугольнике АМРК углы К и М – прямые (как углы между касательной и радиусом). Сумма углов четырехугольника АМРК равна 360 градусов. Угол KLM – вписанный, и его величина равна половине угла КРМ, то есть . Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать Это полезно В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня. Наш онлайн-курс по Физике Все темы ЕГЭ с нуля Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале! Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали. Мы обязательно ответим! Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике. Результат будет выше, если готовиться по отработанной методике. У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей. 🎬 Видео Геометрия Вписанная окружность треугольника ABC касается сторон AB BC и AC в точках M N и KСкачать Задание 16 ЕГЭ по математике #10Скачать Геометрия В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касаетсяСкачать 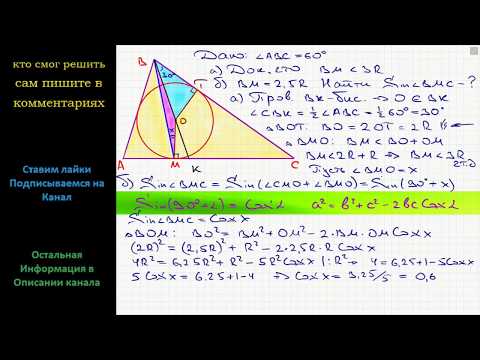Разбор Задачи №16 из Работы СтатГрад от 17 мая 2019Скачать Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать 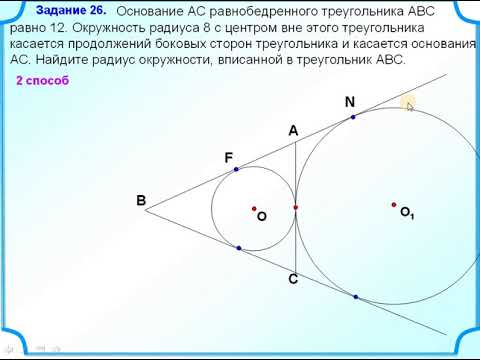Вписанные и описанные окружности. Вебинар | МатематикаСкачать 14.36.1. Планиметрия. Гордин Р.К.Скачать №17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать 13.47.1. Планиметрия. Гордин Р.К.Скачать 8 класс, 38 урок, Вписанная окружностьСкачать 9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать 8.30.1. Планиметрия. Гордин Р.К.Скачать 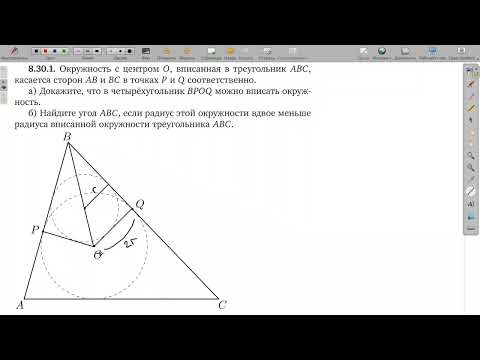Окружность, вписанная в треугольникСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности