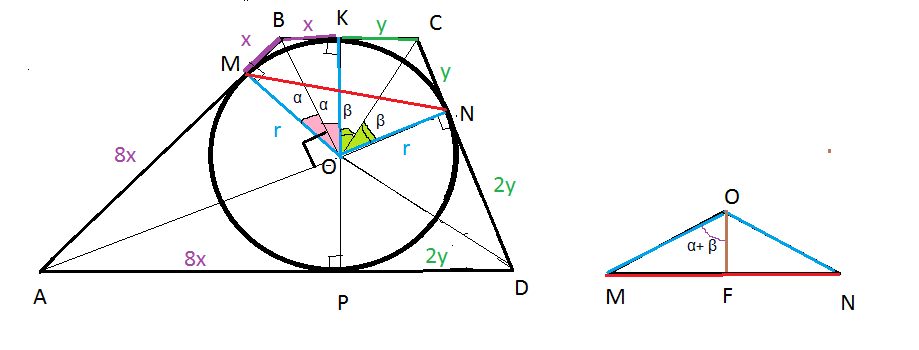
Окружность вписанная в трапецию abcd касается ее боковых сторон (3 видео)

Окружность вписанная в трапецию abcd касается ее боковых сторон

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.

а) Докажите, что AD = 4BC.

б) Найдите длину отрезка MN, если радиус окружности равен

а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.

Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому

то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 8x, DN = 2y.

б) Заметим, что поэтому

Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 4BP, AB = 3BP, BP = 3x, PN = PM = 4x. Прямая PO является серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:

Значит,

Приведем другое решение пункта а)

Пусть окружность касается оснований BC и AD в точках K и L соответственно, ее центр находится в точке O, а BM = x, CN = y, тогда AM = 8x, DN = 2y. Поскольку точки M, K, N и L — точки касания, и Опустим высоты BH и CQ:

тогда по теореме Пифагора Поскольку имеем откуда

Содержание

Задача 16865 Окружность, вписанная в трапецию ABCD.
Условие
Решение
Окружность, вписанная в трапецию ABCD с основаниями AD и ВС, касается боковых сторон АВ и CD в точках F и Т соответственно. Докажите, что AF * FB = СТ * TD.
Ваш ответ
решение вопроса
Похожие вопросы
🌟 Видео

Видео:Трапеция и вписанная окружностьСкачать

Задача 16865 Окружность, вписанная в трапецию ABCD.

Условие

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон АВ и CD в точках М и N соответственно. Известно, что АМ=8МВ и DN=2CN.

а) Докажите, что AD=4BC.

б) Найдите длину отрезка MN, если радиус окружности равен sqrt(6)

Решение

а)
Пусть ВМ=х, тогда АМ=8х
СN=y, тогда DN=2y
По свойству касательной, проведенной к окружности из одной точки, отрезки касательных равны.
Поэтому
ВМ=ВК=x
СN=CK=y
AM=AP=8x
DN=DP=2y

Сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусов.
Биссектрисы АО и ВО делят углы А и В пополам, значит сумма острых углов треугольника АОВ равна 90 градусов.
Треугольник АОВ- прямоугольный.
Высота ОM прямоугольного треугольника АОВ есть среднее пропорциональное между отрезками АМ и ВМ.
ОM^2=AM*BM
OM=r
r^2=8x*x
r^2=8x^2
Аналогично, Δ СOD — прямоугольный и
ON^2=CN*ND
r^2=y*2y
r^2=2y^2

AD=AP+DP=8x+2y=8x+2*2x=12x
BC=BK+CK=x+y=x+2x=3x/(sqrt(x^2+r^2
AD=12x=4*(3x)=4BC

б)
r=sqrt(6)
Обозначим
∠ МОВ= ∠ ВОК= альфа
∠ KOC= ∠ CON= бета
sin альфа =MB/BO=x/sqrt(x^2+r^2)
cos альфа =MO/BO=r/sqrt(x^2+r^2)
sin бета=CN/CO=y/sqrt(y^2+r^2)
cos бета =ON/CO=r/sqrt(y^2+r^2)

sin( альфа + бета )=
=sin альфа*cos бета +cos альфа *sin бета =
=r*(x+y)/(sqrt(x^2+r^2)*sqrt(y^2+r^2))

Треугольник MON — равнобедренный,
МО=ОN=r
∠ MON=2*( альфа + бета )
Высота ОF делит основание MN пополам и сторону MN пополам.
MF=(1/2)MN=OM*sin( альфа + бета )=
MN=2*r*r*(x+y)//(sqrt(x^2+r^2)*sqrt(y^2+r^2))
Так как у=2х и r^2=6 и r^2=8x^2; r^2=2y^2, то
MN=
=2*r^2*((r/sqrt(8))+(r/sqrt(2)))/(r*sqrt((1/8)+1)*r*sqrt((1/2)+1))=
=(2*r*3/(2sqrt(2)))/(sqrt(9/8)*sqrt(3/2))=4

О т в е т. MN=4