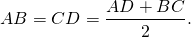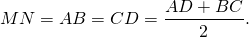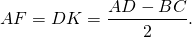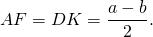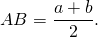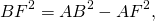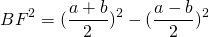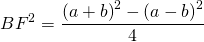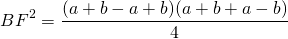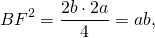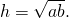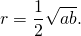Окружность вписанная в равнобокую трапецию делит точкой

Геометрия | 5 — 9 классы

Окружность вписанная в равнобокую трапецию делит точкой касания боковую сторону на отрезки длиной 2 см и 32 см.

Отрезки касательных, проведённые из одной точки, равны, значит, одна боковая сторона равна 2 + 32 = 34, вторая равна ей, меньшее основание равно 2 + 2 = 4, большее равно 32 + 32 = 64.

Проводим две высоты к большему основанию, а также диаметр, перпендикулярный к основанию.

Высоты и перпендикуляр параллельны, кроме того, отрезки высот отсекают на большем основании три отрезка, два из которых соответственно равны, а третий равен меньшему основанию, т.

Значит, равные отрезки, на которые делят высоты большее основание равны 1 / 2 * (64 — 4) = 30.

Далее по теореме Пифагора находим высоту, т.

Е. катет прямоугольного треугольника, который равен √(34² — 30²) = √(1156 — 900) = √256 = 16.

Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее большее основаниеСкачать

Окружность, вписанная в прямоугольную трапецию, делит точкой большую боковую сторону на отрезки длиной 4 см и 25 см?

Окружность, вписанная в прямоугольную трапецию, делит точкой большую боковую сторону на отрезки длиной 4 см и 25 см.

Найдите высоту трапеции.

Видео:Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать

Окружность, вписанная в прямоугольную трапецию, делит точкой касания большую боковую сторону на отрезки длиной 4 см и 25 см?

Окружность, вписанная в прямоугольную трапецию, делит точкой касания большую боковую сторону на отрезки длиной 4 см и 25 см.

Найдите высоту трапеции!

Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее меньшее основаниеСкачать

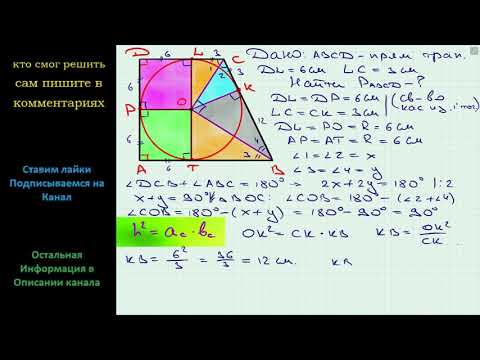
Около окружности описана равнобокая трапеция у которой боковая сторона точкой касания делится на отрезки 3 см и 8 см?

Около окружности описана равнобокая трапеция у которой боковая сторона точкой касания делится на отрезки 3 см и 8 см.

Найдите площадь трапеции.

И если можно с обяснением.

Видео:Трапеция и вписанная окружностьСкачать

Окружность вписанная в равнобокую трапецию делит точкой касания боковую сторону на отрезки, меньший из которых = 5см?

Окружность вписанная в равнобокую трапецию делит точкой касания боковую сторону на отрезки, меньший из которых = 5см.

Найти большее основание трапеции, если её Р = 56см.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В прямоугольную трапецию вписана окружность?

В прямоугольную трапецию вписана окружность.

Точка касания делит большую боковую сторону на отрезки длиной 8 см и 18см .

Найдите периметр трапеции.

Видео:Геометрия В равнобокую трапецию вписана окружность. Точка касания делит боковую сторону на отрезкиСкачать

В прямоугольную трапецию вписана окружность?

В прямоугольную трапецию вписана окружность.

Точка касания окружности

с боковой стороной делит эту сторону на отрезки с длинами 4 и 9.

Найти площадь трапеции.

Видео:Окружность, вписанная в трапециюСкачать

Окружность, вписанная в равнобокую трапецию, делит точки касания боковую сторону на отрезки, длина большого из которых равна 8 см?

Окружность, вписанная в равнобокую трапецию, делит точки касания боковую сторону на отрезки, длина большого из которых равна 8 см.

Найдите меньшее основание трапеции, если её периметр равен 60 см.

Видео:ЕГЭ Математика Задание 6#27935Скачать

Около окружности описана равнобокая трапеция у которой боковая сторона точкой касания делится на отрезки 2 см и 8 см?

Около окружности описана равнобокая трапеция у которой боковая сторона точкой касания делится на отрезки 2 см и 8 см.

Найдите площадь трапеции.

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

100 БАЛЛОВ?

В РАВНОБОКУЮ ТРАПЕЦИЮ С БОКОВОЙ СТОРОНОЙ, РАВНОЙ 18, ВПИСАНА ОКРУЖНОСТЬ.

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ КАСАНИЯ ОКРУЖНОСТИ С БОКОВЫМИ СТОРОНАМИ РАВНО 8.

НАЙДИТЕ РАДИУС ОКРУЖНОСТИ.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

В равнобедренную трапецию вписана окружность?

В равнобедренную трапецию вписана окружность.

Найдите среднюю линию трапеции, если точка касания окружности делит боковую сторону трапеции на отрезки, равные 2 и 4.

На этой странице находится ответ на вопрос Окружность вписанная в равнобокую трапецию делит точкой касания боковую сторону на отрезки длиной 2 см и 32 см?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Сумма углов треугольника равна 180°. Величина тупого угла больше 90°, но меньше 180°. Значит на два других угла остается меньше 90°. Значит эти два угла могут быть только острыми.

Прости за качество ) Решение на фотографии.

Представьте, что это ровные круги) если совсем непонятно : один круг с радиусом в 4 клетки, второй — 3 клетки. Поставьте циркуль и отведите второй конец на 4 клетки, потом уменьшите на одну клетку, не убирая циркуль, и проведите второй круг.

Пусть ВС = х см, тогда АВ = (х + 6) см. Р = 2 * (АВ + ВС) 2 * (х + 6 + х) = 48 2х + 6 = 48 : 2 2х + 6 = 24 2х = 24 — 6 2х = 18 х = 18 : 2 х = 9 ВС = 9 см АВ = 9 + 6 = 15см Противоположные стороны параллелограмма равны Ответ : АВ = СД = 15см, ВС = АД..

Пусть х одна сторона. Тогда х + 2 вторая сторона. Зная, что Р = 36, составим уравнение : 2х + 2х + 4 = 364х = 32Х = 8 см. Одна сторона 8 см, значит другая 8 + 2 = 10 см. S = 3×10 = 30см ^ 2Ответ 30.

Условия задач даны на фото.

В этом треугольнике 6² = 3² + (3√3)² то есть 36 = 9 + 27 36 = 36 Значит треугольник ABC — прямоугольный, а радиус окружности описанной около прямоугольного треугольника равен половине гипотенузы. Гипотенуза в этом треугольнике AC = 6, значит R = 1 /..

Вот посмотри если в первом что то не понятно мне все равно я свое дело сделал.

Значит так, у нас есть смежные и верти кальные углы смежные в сумме дают 180 градусов, а вертикальные равны если ты нарисуешь крестик , то верхние углы смежные значит 180 — 94 ты получаешь 2 угол вертикальные углы это 1. 2 + 3. 4. Углы 3 и 2 , и4 и..

Сумма двух углов по одной стороне параллелограмма = 180° 1) если один угол = х°, то другой = 2х (по условию) х + 2х = 180 3х = 180 х = 60 2х = 120 Противолежащие углы параллелограмма равны, ⇒ углы параллелограмма = 60° ; 120° ; 60° ; 120° — — — — — -..

Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

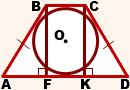
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Задача про трапецию, описанную около окружностиСкачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Окружность, вписанная в трапецию.A circle inscribed in a trapezoid.Скачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

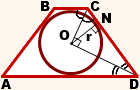
Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Планиметрия 3 | mathus.ru | трапеция и окружностьСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

📽️ Видео

Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Планиметрия 38 | mathus.ru | окружность вписана в равнобедрунную трапецию | отношение площадейСкачать

Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать