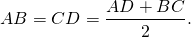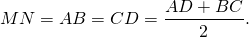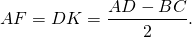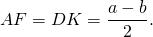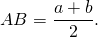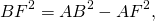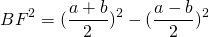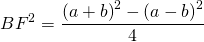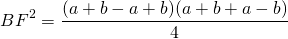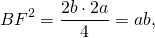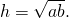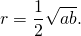Окружность вписанная в равнобедренную трапецию касается боковых сторон

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.

а) Докажите, что AD = 4BC.

б) Найдите длину отрезка MN, если радиус окружности равен

а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.

Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому

то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 8x, DN = 2y.

б) Заметим, что поэтому

Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 4BP, AB = 3BP, BP = 3x, PN = PM = 4x. Прямая PO является серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:

Значит,

Приведем другое решение пункта а)

Пусть окружность касается оснований BC и AD в точках K и L соответственно, ее центр находится в точке O, а BM = x, CN = y, тогда AM = 8x, DN = 2y. Поскольку точки M, K, N и L — точки касания, и Опустим высоты BH и CQ:

тогда по теореме Пифагора Поскольку имеем откуда

Видео:14.43.1. Планиметрия. Гордин Р.К.Скачать

Окружность, вписанная в равнобедренную трапецию ABCD, касается боковых сторон АВ и CD в точках M и N соответственно?

Геометрия | 10 — 11 классы

Окружность, вписанная в равнобедренную трапецию ABCD, касается боковых сторон АВ и CD в точках M и N соответственно.

Отрезок AN пересекает окружность в точке K, а луч MK пересекает основание AD в точке L.

А) Докажите, что треугольники AKL и МAL подобны.

Б) Найдите отношение AL : LD.

A) Из симметрии всей этой «конструкции» MN II AD ; поэтому ∠KAL = ∠MNK ; но ∠MNK = ∠AMK ; (поскольку эти углы «измеряются» половиной дуги MK) ;

то есть у треугольников AKL и MAL ∠ALM общий, а ∠AML = ∠KAL ; следовательно эти треугольники подобны по двум углам.

Б) Из той же симметрии следует ∠KAL = ∠MDA ; = &gt ; ∠MDA = ∠AML ; то есть получается, что есть еще один треугольник, подобный AKL и MAL — это треугольник AMD ;

то есть AL / AM = AM / AD ;

Если обозначить P — точка касания AD с окружностью, то AM = AP ; и (опять таки — из симетрии : ) ) AP = AD / 2 ;

получилось AM = AD / 2 ;

AL = AM ^ 2 / AD = AD / 4 ; AL / AD = 1 / 4 ;

довольно странный результат — получается L — середина AP ;

Видео:Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать

Продолжения равных хорд АВ и СD окружности соответственно за точки В и С пересекаются в точке Р?

Продолжения равных хорд АВ и СD окружности соответственно за точки В и С пересекаются в точке Р.

Докажите, что треугольник АРD равнобедренный.

Видео:ЕГЭ Математика Задание 6#27935Скачать

Диагонали равнобедренной трапеции ABCD с боковой стороной AB пересекаются в точке P?

Диагонали равнобедренной трапеции ABCD с боковой стороной AB пересекаются в точке P.

Докажите , что центр описанной около неё окружности лежит на окружности , описанной около треугольника APB.

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Окружность радиуса 12 вписана в равнобедренную трапецию?

Окружность радиуса 12 вписана в равнобедренную трапецию.

Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4.

Найдите периметр трапеции.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

ABCD — Равнобедренная трапеция с основаниями AD и BC, диагонали которой пересекаются в точке О?

ABCD — Равнобедренная трапеция с основаниями AD и BC, диагонали которой пересекаются в точке О.

Докажите, что треугольники AOD и BOC подобны.

Видео:ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать

Окружность, вписанная в равнобедренный треугольник АВС, касается основания АС в точке М и боковой стороны в точке N?

Окружность, вписанная в равнобедренный треугольник АВС, касается основания АС в точке М и боковой стороны в точке N.

Отрезки ВМ и СN пересекаются в точке К.

Найти радиус окружности, вписанной в треугольник АВС, если известно, что АВ = 5 и СК : КN = 5 : 1.

Видео:Трапеция и вписанная окружностьСкачать

Окружность вписанная в равнобедренный треугольник касается боковых сторон в точках m и k?

Окружность вписанная в равнобедренный треугольник касается боковых сторон в точках m и k.

Найдите длину отрезка MK если основание треугольник равно 16 а боковая сторона 10.

Видео:Окружность, вписанная в трапециюСкачать

В равнобедренно треугольнике ABC с основанием АС вписана окружность с центром О?

В равнобедренно треугольнике ABC с основанием АС вписана окружность с центром О.

Луч СО пересекает сторону АВ в точке К, причем АК = 6, ВК = 12.

Найдите периметр треугольника .

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

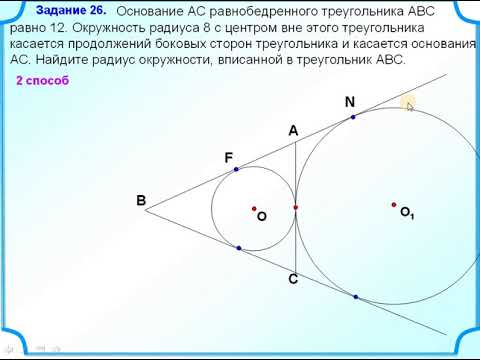
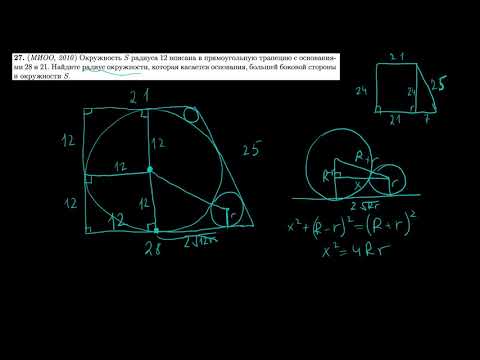
Внутри равнобедренной трапеции ABCD с основаниями BC = 12, AD = 28 и боковой стороной CD = 10 выбрана точко О так, что окружность с центром в точке О касается оснований трапеции и стороны CD ?

Внутри равнобедренной трапеции ABCD с основаниями BC = 12, AD = 28 и боковой стороной CD = 10 выбрана точко О так, что окружность с центром в точке О касается оснований трапеции и стороны CD .

Найдите площадь треугольника ABO.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Равнобедренная трапеция ABCD с основаниями AD и BC описана около окружности?

Равнобедренная трапеция ABCD с основаниями AD и BC описана около окружности.

Сторона CD касается этой окружности в точке Q, a отрезок AQ пересекает окружность в точке P.

Найти радиус окружности, если известно, что AP = 2, PQ = 7.

Видео:ЭКЗАМЕН КАНАДА. Покажи, как нужно решать!Скачать

Две прямые, касающиеся данной окружности в точках А и В, пересекаются в точке С?

Две прямые, касающиеся данной окружности в точках А и В, пересекаются в точке С.

Докажите, что центр окружности, вписанной в треугольник АВС, лежит на данной окружности.

Вы зашли на страницу вопроса Окружность, вписанная в равнобедренную трапецию ABCD, касается боковых сторон АВ и CD в точках M и N соответственно?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Периметр прямоугольника рассчитывается по формуле : P = 2(a + b) Подставим значения a и b в формулу и получим : P = 2(10 + 8) = 36 см Ответ : 36 см.

Три прямые пересекаются в одной точке и образуют шесть углов. Найдите сумму трёх из этих углов, которые попарно не имеют общих точек.

Известно : биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (в нашем случае — катетам), т. Е. дано отношение катетов 15 : 20 = 3 : 4 отношение катетов — — это тангенс острого угла в прямоугольном треугольнике и..

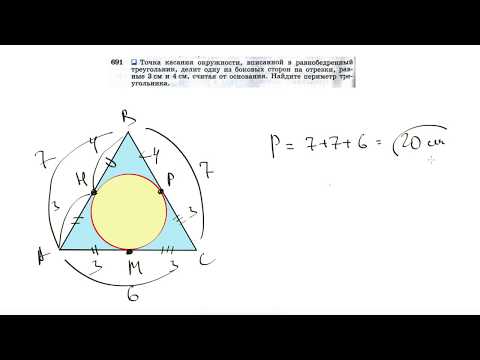
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

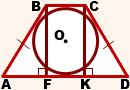
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

🌟 Видео

9.56.1. Планиметрия. Гордин Р.К.Скачать

Задание 16 ЕГЭ по математике #6Скачать

Задание 26 Трапеция ОкружностьСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

ЕГЭ Задание 16 Равнобедренная трапеция Вписанные окружностиСкачать

Задача об эллипсе, вписанном в равнобедренную трапециюСкачать

Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать

Геометрия Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром OСкачать