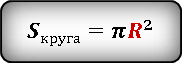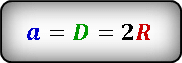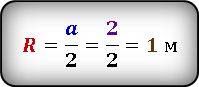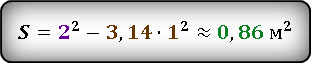
Окружность в квадрате задача (2 видео) | Курс школьной геометрии

Квадратура круга

Несомненно, циркуль и линейка — весьма полезные и эффективные инструменты, с помощью которых можно «построить», пожалуй, все, что угодно. Однако есть задачи, которые им не под силу. Одна из них — задача о квадратуре круга, которая вместе с трисекцией угла и удвоением куба, считается не только самой сложной, но и наиболее древней задачей, не имеющей решения.

Круг и квадрат одинаковой площади.

Жившие около двух тысяч лет назад египетские и вавилонские математики пытались с помощью циркуля и линейки построить квадрат, площадь которого была бы равна площади данного круга, и, судя по древнему папирусу, им это удалось (сторона квадрата должна быть равна 8/9 диаметра круга). В Древней Греции не только геометры, но и философы уделяли много времени задаче, получившей название квадратуры круга, и даже, по свидетельству Плутарха — древнегреческого историка, одному из них — Антифонту — удалось найти решение. Перед тем, как заниматься кругом, философ решил построить квадрат, равновеликий по площади многоугольнику: Антифонт последовательно удваивал стороны многоугольника до тех пор, пока не получилось такое число сторон, что они совпали с дугами окружности. Добившись успеха с многоугольником, философ научно обосновал возможность построить квадрат и для круга, однако никаких доступных свидетельств этого не сохранилось.

Следующим человеком, совершившим существенный переворот в решении задачи о квадратуре круга, был Гиппократ Хиосский, обнаруживший пропорциональность площади круга квадрату его диаметра. Несмотря на то, что это предположение так и осталось гипотезой, именно благодаря ему Гиппократ открыл квадратируемые фигуры (их площади выражались в рациональных числах), которые ограничены пересекающимися окружностями. Ученому удалось получить общий для всех кругов коэффициент пропорциональности, названный позже «гиппократовыми луночками», который мог бы помочь в решении задачи в том случае, если бы круг можно было бы разбить на квадраты.

Некоторые математики пытались использовать для построения квадрата не только циркуль и линейку, но и другие — не только существующие, но и специально изобретенные для этой задачи инструменты, а также специальные кривые, самая известная из которых — квадратриса Динострата, придуманная Гиппием из Элиды. Однако, невзирая на все уловки, задача о квадратуре круга, которая в результате была сведена к поискам точного отношения длины окружности к ее диаметру, не поддалась ни одному пытливому уму. Единственное, что было найдено, так это весьма приблизительное решение задачи: диаметр окружности, в которую вписан квадрат, утраивается и складывается с 1/5 части стороны квадрата.

Немало линеек и циркулей было сломано неутомимыми математиками в поисках решения задачи о квадратуре круга, и только в конце XIX века немецким математиком Ф. Линдеманом было получено доказательство того, что эта знаменитая задача может быть решена только лишь (и никак иначе!) с привлечением дополнительных инструментов. Возможно, именно с этого времени словосочетание «квадратура круга» приобрела метафорическое значение неразрешимой задачи или безнадежного дела.

Содержание

Квадратура круга: наглядное доказательство
Задача: окружность вписана в квадрат , определить площадь закрашенной области
Условие задачи:
Найти площадь закрашенной области: S
Ответ:
💡 Видео

Видео:Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Квадратура круга: наглядное доказательство

Словесные доказательства с трудом даются тем, кто привык мыслить визуально. Поэтому в математике так важна визуальная интуиция. Доказательства из таких пособий, как и «Евклид Начала: первые 6 книг» и «Доказательства без слов: учебник по визуальному мышлению» даются пониманию при взгляде на их страницы. Я рекомендую эти книги к прочтению каждому, кто интересуется доказательствами других математических проблем.

К примеру, мы помним из школьного курса, что площадь круга вычисляется по формуле π x r², но можем ли мы доказать, что эта формула справедлива для каждой возможной окружности?

Величайший из математиков Евклид нашёл доказательства этой формулы настолько простое, что теперь студенты изучают начала интегрального исчисления по нему. Евклид рассуждал так: круг можно поделить на четыре, шесть, шестнадцать, или бесконечно много равных частей, а потом расставить их так, чтобы получился прямоугольник.

Первое что нам нужно сделать — начертить окружность. Затем, мы разделим круг на 8 равных частей и расставим их в похожую на прямоугольник форму. Мы почти получили прямоугольник.

Повторим процесс, на этот раз с 32 равными частями. Если расставить их таким же образом как в предыдущем примере, то мы получим что-то ещё более похожее на прямоугольник.

Это значит, что если разделить круг на ещё больше равных частей — происходит удивительное, форма начинает приближаться к идеальному прямоугольнику.

Насколько много должно быть частей чтобы получить идеальный прямоугольник? Для этого его части должны быть бесконечно малыми — такими, что невозможно различить толщину, и стороны становятся почти вертикальными.

Мы знаем, что площадь прямоугольника это его ширина x высота . Высота прямоугольника будет равна радиусу окружности. Чтобы найти ширину, нужно знать длину окружности. Если сравнить ширину прямоугольника и окружность, видно, что ширина это половина от длины окружности. Для длины окружности равной 2πr следует, что ширина должна быть πr.

Выражение ширина x высота означает тоже самое что π x r x r . Иными словами — квадрат радиуса, умноженный на π, то есть πr². Это и есть искомый прямоугольник, площадь которого равна площади круга.

Таким образом, πr² может использоваться для вычисления площади любой из существующих окружностей.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

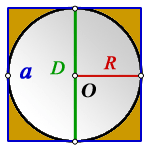
Задача: окружность вписана в квадрат , определить площадь закрашенной области

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Условие задачи:

Окружность вписана в квадрат. Найти площадь закрашенной области, если сторона квадрата равна 2 м.

Дано:
Сторона квадрата, a = 2 м

Пояснение к рисунку:
O — центр окружности
R — радиус окружности
D — диаметр окружности

Видео:Площадь круга. Математика 6 класс.Скачать

Найти площадь закрашенной области: S

Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга

Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу

Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.

Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.

Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Ответ:

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Если в уже полученное выражение подставить формулу площади круга выраженную через сторону квадрата и преобразовав, получим следующую формулу, в которой площадь закрашенной области, будет сразу выражена через сторону квадрата.