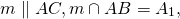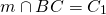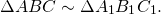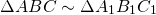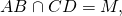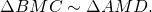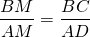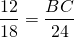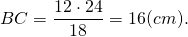Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него треугольник, подобный данному.


1) ∠BAC=∠BA1C1 (как соответственные при AC ∥ A1C1 и секущей AB)
Следовательно, треугольники подобны:
Что и требовалось доказать .
Продолжения боковых сторон AB и CD трапеции пересекаются в точке M. Большее основание трапеции AD равно 24 см, МС=5 см, CD=7см. Найдите меньшее основание трапеции.

AD=24 см, BM=12 см, AB=6 см
В треугольнике AMD BC — прямая, параллельная стороне AD и пересекающая две другие его стороны AM и DM. Следовательно, она отсекает от него подобный треугольник:
Из подобия треугольников следует пропорциональность их соответствующих сторон:
Если бы в задаче вместо AD и BC была задействована зависимость между MC и MD, достаточно было бы применить обобщенную теорему Фалеса для угла AMD:
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подобные треугольники
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Подобные треугольники
Подобные треугольники — это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.
Сходственные стороны — это стороны двух треугольников, лежащие против равных углов.
Рассмотрим два треугольника 

Стороны AB и A1B1, BC и B1C1, CA и C1A1, лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:
| AB | = | BC | = | AC | = k, |
| A1B1 | B1C1 | A1C1 |
k — это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если k = 1, то треугольники равны, то есть равенство треугольников – это частный случай подобия.
Подобие треугольников обозначается знаком
: 

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S1, то:
| S | = k 2 . |
| S1 |
Видео:Треугольники. 7 класс.Скачать

Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам другого, то треугольники подобны.
то 

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.
| Если | AB | = | AC | , ∠A = ∠A1, |
| A1B1 | A1C1 | |||
то  ABC ABC
| ||||
Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.
📽️ Видео
Параллельные прямые (задачи).Скачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

№52. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторонаСкачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать

№794. Сторона АВ треугольника ABC разделена на четыре равные части и через точки деления проведеныСкачать

Признаки равенства треугольников. 7 класс.Скачать

Задача, которую боятсяСкачать

Параллельные прямые. 6 класс.Скачать