Окружность с центром в точке о пересекает луч ок

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Ваш ответ

Видео:2184 касательная в точках A и B к окружности с центром О пересекаютсяСкачать

решение вопроса

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Круг. Окружность (центр, радиус, диаметр)Скачать

29.09.2020 Геометрия 9 класс математическая вертикаль ответы и задания

ПОДЕЛИТЬСЯ

Ответы и задания для итоговой диагностической работы по геометрии 9 класс за 8 класс проект математическая вертикаль 2 варианта. Официальная дата проведения работы: 29.09.2020 (29 сентября 2020 год).

Ссылка для скачивания вариантов: скачать задания

Ссылка для скачивания ответов для вариантов: скачать ответы

Решать варианты математической вертикали по геометрии 9 класс:

1)Укажите про каждое из утверждений верное оно или нет.

• а) (1 балл) Если в тупоугольном треугольнике ABC (∠B — тупой) проведена высота AH; AH = 6, BC = 10, то его площадь равна 30.
• б) (1 балл) Отрезок, соединяющий середины противоположных сторон ромба, равен полусумме этих сторон.
• в) (1 балл) Если в параллелограмм можно вписать окружность, то он является квадратом.
• г) (1 балл) Если градусная мера дуги окружности больше 200°, то эта дуга больше половины этой окружности.

2)Дан ромб ABCD, ∠ABC + ∠BCD + ∠ВAD = 235°. Найдите угол BAD.

3)Окружность с центром в точке О пересекает луч OK в точке M. Дуга MN равна 134°. Найдите угол NMK.

4)На расстоянии 15 метров расположены 2 столба высотой 12 метров и 20 метров. Найдите расстояние между вершинами столбов.

5)На стороне AB параллелограмма ABCD отмечена такая точка K, что AK : KB = 1 : 2. Найдите площадь четырехугольника AKCD, если площадь параллелограмма ABCD равна 24.

6)На стороне AC треугольника ABC отмечена точка D; CD = 4, AD = 5, 6∠A = 3∠ABD = 2∠ABC. Найдите BC.

7)В окружности проведен диаметр AC. Через точку B (отличную от A и С), лежащую на окружности, провели касательную, AT — перпендикуляр, опущенный на эту касательную. Докажите, что AB — биссектриса угла TAC.

8)Укажите про каждое из утверждений верное оно или нет. а) (1 балл) Если в прямоугольном треугольнике ABC (∠B — прямой) AB = 8, AC = 12, то его площадь равна 48. б) (1 балл) Средняя линия трапеции равна полусумме сторон, которые она соединяет. в) (1 балл) Если трапеция равнобокая, то ее можно вписать в окружность. г) (1 балл) Если градусная мера дуги окружности меньше 180°, то на неё опирается острый центральный угол.

9)Дан ромб ABCD, ∠DAB + ∠ABC + ∠BCD = 248°. Найдите угол BСD.

10)Окружность с центром в точке О пересекает луч ОК в точке М. Дуга MN равна 138°. Найдите угол NMK.

11)На расстоянии 12 метров расположены 2 столба высотой 15 метров и 20 метров. Найдите расстояние между вершинами столбов.

12)На стороне CD параллелограмма ABCD отмечена такая точка K, что CK : KD = 1 : 2. Найдите площадь четырехугольника ABCK, если площадь параллелограмма ABCD равна 18.

13)На стороне AB треугольника ABC отмечена точка D; BD = 5, AD = 15, 12∠A = 4∠ACD = 3∠ACB. Найдите BC

14)В окружности проведен диаметр AC. Через точку B (отличную от A и С), лежащую на окружности, провели касательную; AT — перпендикуляр, опущенный на эту касательную. Докажите, что AB — биссектриса угла TAC.

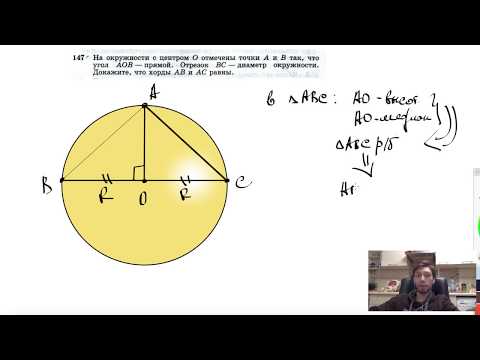
Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

Презентация по геометрии » ПЛАНИМЕТРИЯ НА ЕДИНОМ ГОСУДАРСТВЕННОМ ЭКЗАМЕНЕ ПО МАТЕМАТИКЕ»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

ПЛАНИМЕТРИЯ НА ЕДИНОМ ГОСУДАРСТВЕННОМ ЭКЗАМЕНЕ Презентация выполнена по материалам статьи И.К. Варшавского, М.Я.Гаиашвили, Ю.А.Глазкова в журнале « Математика в школе» №2, 2001г.

Во многих задачах встречается окружность, касающаяся сторон угла. Напомним, что в этом случае Центр окружности лежит на биссектрисе угла (О ϵ b). Отрезки, соединяющие точки качания с центром окружности, являются ее радиусами и перпендикулярны к сторонам угла (ОА = ОС = r, ОА ﬩ ВА, ОС ﬩ ВС). Равны расстояния от вершины угла до точек касания (ВА=ВС). ∠АВС + ∠АОС = 180˚. Даже этот краткий перечень свойств позволяет решать большое количество разнообразных задач.

Пример 1 Так как ОА ﬩ ВА, то в треугольнике АВО АВ= =24. Тогда ВА = 24. В треугольнике АВС отрезок ВН – биссектриса и ВА = ВС, следовательно, ВН ﬩ АС и АН = СН. Найдем высоту АН прямоугольного треугольника АВО: АН · ВО = ВА · ОА, значит, = 6,72. Тогда АС = 2АН = 13,44. Ответ: 13,44. Окружность с центром О касается сторон угла В в точках А и С. Радиус окружности равен 7, ВО = 25. Найдите АС. Решение

Пример 2 Окружность с центром О касается сторон угла В в точках А и С. Радиус окружности равен 6, ВО = 2АО. Найдите площадь треугольника АОС. Решение Прежде всего отметим, что на чертеже к данной задаче совсем необязательно изображать окружность, поскольку важно представить лишь взаимное расположение отрезков и точек. В прямоугольнике АВО ВО = 2АО, следовательно, ∠АВО = 30˚. Отсюда получаем: ∠АВС=2∠АВО=60˚ и ∠АОС = 180˚- 60˚ = 120˚. SАОС = АО · СО · = · 36 · = 9 . Ответ: 9 .

Пример 3 Отрезок ВО – биссектриса треугольника АВМ, следовательно, ВА : АО = ВМ : МО = 18 : 9 = 2 : 1. Пусть АО = x, тогда АВ = 2х, и в прямоугольном треугольнике АВМ: 182 = (х + 9)2 + (2х)2. Далее получаем: 5х2 + 18х — 243 = 0. Положительный корень уравнения равен 5,4. Следовательно, АО = 5,4, ВА = 10,8. SВОМ = ВА · ОМ = · 10,8 · 9 = 48,6. Ответ: 48,6. Окружность с центром О касается сторон угла В в точках А и С. Лучи АО и ВС пересекаются в точке М, ОМ = 9, ВМ = 18. Найдите площадь ВОМ. Решение

Пример 4 Окружность с центром О касается сторон угла В в точках А и С. Отрезок ВО пересекает окружность в точке К. Найдите периметр четырехугольника АКСО, если ∠В = 60˚, ВК = 12. Решение Пусть КО = r. В прямоугольном треугольнике АВО ∠АВО= АВС=30˚, следовательно, ВК + КО = 2АО, т.е. ВК + r = 2r. Отсюда получаем: r = ВК = 12. В прямоугольном треугольнике АВО ∠АОВ = 90˚ — ∠АВО = 60˚. Так как в треугольнике АОК ∠О = 60˚ и АО = ОК, то треугольник равносторонний. Значит, АК = r = 12. Аналогично получаем, что СК = r = 12.Итак, периметр четырехугольника АКСО равен 48. Ответ: 48.

Если окружность вписана в треугольник или четырехугольник, то она касается сторон всех его углов, поэтому на основе перечисленных выше свойств окружности, вписанной в угол, получаем: Центр окружности является точкой пересечения биссектрис углов треугольника (четырехугольника). Радиусы, проведенные в точки касания, перпендикулярны к сторонам треугольника (четырехугольника). Равны расстояния от вершины угла до точек касания.

Пример 5 Данная Окружность касается сторон угла А в точках Т и М, следовательно, АТ = АМ. Тогда ВТ = АВ – АТ = АС – АМ = МС. Пусть окружность касается стороны ВС в точке Н. Тогда ВТ = ВН и СМ = СН. Следовательно, ВН = ВТ = СМ = СН = 14 : 2 = 7 и АТ = АМ = 25 – 7 = 18. Так как равнобедренные треугольники АТМ и АВС подобны (почему?), имеем: = . Следовательно, ТМ = = = 10,08. Решение Окружность, вписанная в равнобедренный треугольник АВС, касается его боковых сторон АВ и АС в точках Т и М соответственно. Найдите ТМ, если АВ = 25, ВС = 14. Ответ: 10,08.

Пример 6 Луч ВМ = биссектриса угла В, значит, АМ : СМ = АВ : СВ = 5 : 3. Пусть АМ = 5х, тогда СМ = 3х и АС = 8х. Треугольники АТМ и АВС подобны (почему?), следовательно = , т.е. ТМ = = 3,75. Ответ: 3,75. В треугольник АВС вписана окружность с центром О. Лучи ВО и СО пересекают стороны АС и АВ в точках М и Т соответственно. Найдите МТ, если АВ = АС = 10, ВС = 6. Решение

Пример 7 Пусть луч АО пересекает сторону ВС в точке Н, тогда отрезок АН — биссектриса треугольника АВС. По условию АВ = АС, следовательно, ВН = НС = 8 и АН ﬩ ВС. В прямоугольном треугольнике АВН АН = = 6. Луч ВО – биссектриса угла В, а, значит, отрезок ВО – биссектриса треугольника АВН, поэтому АО : ОН = АВ : ВН = 5 : 4. Пусть АО = 5х, тогда ОН = 4х и АН = 9х. Треугольники АТО и АВН подобны (почему?), следовательно, = . Отсюда получаем: ТО = = = . Значит, ТМ = = 8 . Ответ: 8 . В треугольник АВС вписана окружность с центром О. Прямая, проходящая через точку О параллельно прямой ВС, пересекает стороны АС и АВ в точках М и Т соответственно. Найдите МТ, если АВ = АС = 10, ВС = 16. Решение

. Пример задачи № 7, как и многие геометрические задачи, можно решить несколькими способами. Например, для вычисления отрезка ОН можно использовать формулы S = pr и S = , где S — площадь треугольника, r – радиус вписанной окружности, h — высота треугольника, а – сторона, к которой проведена высота h. Замечание. Возвращаясь к чертежам задач 5, 6 и 7, отметим, что на каждом из них точка М располагается иначе, чем в других задачах (рис. 9). Особенно важно помнить, что в общем случае точка пересечения стороны с биссектрисой треугольника (M1) и точка касания стороны с вписанной окружностью (М2) не совпадают. Их совпадение возможно только на основании равнобедренного треугольника (точка Н). Еще одно интересное соотношение для радиуса окружности, вписанной в равнобедренный треугольник, легко получить, применяя подобие. Рассмотрим равнобедренный треугольник АВС с основанием ВС. Центр окружности лежит на биссектрисе АН, являющейся также высотой и медианой треугольника. Прямоугольные треугольники АОТ и АВН подобны (почему?), следовательно, ТО : ВН = АТ : АН. Из пропорции получаем r = . Аналогично получается формула r = .

Задачи для самостоятельного решения Задача 1. Окружность касается одной стороны прямого угла с вершиной А в точке О и пересекает его вторую сторону в точке С. Найдите радиус окружности, если АВ = 4, АС = 8. Задача 2. Из точки М к окружности с центром О проведены прямая МО и касательная МА (А – точка касания). Из точки А к прямой МО проведен перпендикуляр АВ. Найдите расстояние от точки М до центра, если АМ = 40 и АВ = 24. Задача 3. Через точку внутри круга радиуса 10 проведены две взаимно перпендикулярные хорды длиной 16 и 12. Найдите расстояние между серединами хорд. Задача 4. Две параллельные хорды окружности отсекают от нее дуги в 90˚. Длина одной из хорд равна 8. Найдите расстояние между хордами. Задача 5. Через середину радиуса окружности проведена перпендикулярная ему хорда. Найдите градусную меру меньшей из дуг, на которые окружность делится проведенной хордой. Задача 6. Основание равнобедренного треугольника вдвое меньше его боковой стороны, а высота, проведенная к основанию, равна 10. Найдите радиус вписанной в треугольник окружности. Задача 7. Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках M и N. Точка М делит сторону на отрезки 18 и 12, считая от основания треугольника. Найдите MN.

Опыт работы показывает, что методика, предложенная авторами, очень помогает при подготовке к ЕГЭ по математике. Учитель: Гудкова В.Д.

📺 Видео

5 класс, 22 урок, Окружность и кругСкачать

ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать

Окружность. 7 класс.Скачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Длина окружности. Математика 6 класс.Скачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Окружность. Круг. 5 класс.Скачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

Геометрия В трапеции ABCD (ABllCD) угол ABC равен 130. Окружность с центром в точке B проходит черезСкачать

Окружность описана около равнобедренного треугольника. Найти центральный уголСкачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

Найти центр и радиус окружностиСкачать