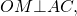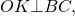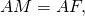Окружность с центром о вписанная в треугольник касается стороны (8 видео)

Окружность с центром о вписанная в треугольник касается стороны

Окружность с центром O, вписанная в треугольник ABC, касается стороны BC в точке P и пересекает отрезок BO в точке Q. При этом отрезки OC и QP параллельны.

а) Докажите, что треугольник ABC ― равнобедренный.

б) Найдите площадь треугольника BQP, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2a.

Пусть луч BO пересекает сторону AC в точке D. Введем следующие обозначения: ∠BCO = ∠DCO = α, ∠COP = x. Прямые OC и QP параллельны, а углы COP и OPQ ― накрест лежащие при пересечении прямых PQ и OC секущей OP, следовательно, ∠OPQ = x. Далее, из прямоугольного треугольника OPC находим а из равнобедренного треугольника OPQ находим ∠POQ = π − 2x = 2α. Таким образом, треугольники BOP и BCD подобны, и, значит, биссектриса BD треугольника ABC является его высотой, откуда следует, что треугольник ABC ― равнобедренный треугольник, что и требовалось доказать.

б) Отрезок CO ― биссектриса треугольника BCD, следовательно:

Далее CP = DC = a, значит, BP = 2a и, следовательно, Откуда

следовательно

По формуле Герона находим: Значит,

Ответ :

Приведем решение пункта б) Данила Касьяненко.

По условию тогда так как Проведем через точку Q прямую, параллельную прямой АС, пусть она пересечет сторону ВС в точке N. Тогда QN — средняя линия треугольника BDC, поэтому а По свойству касательных и тогда

Из прямоугольного треугольника BQN найдем BQ:

Проведем QT перпендикулярно CB. Из прямоугольного треугольника BQN найдем QT:

Найдем площадь треугольника BQP:

Критерии оценивания выполнения задания

Баллы

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)

Получен обоснованный ответ в пункте б)

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

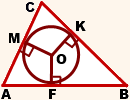
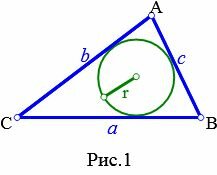
Имеется верное доказательство утверждения пункта а)

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Содержание

Окружность, вписанная в треугольник
Окружность, вписанная в треугольник
Определение окружности, вписанной в треугольник
Теорема об окружности, вписанной в треугольник
🌟 Видео

Видео:Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать

Окружность, вписанная в треугольник

Что такое окружность, вписанная в треугольник? Какие у вписанной окружности свойства?

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Общие точки окружности и треугольника называются точками касания.

Запись окр. (O; r) читают: «Окружность с центром в точке O и радиусом r».

На рисунке окр. (O; r) — вписанная в треугольник ABC.

M, K, F- точки касания.

Свойства вписанной в треугольник окружности.

1) Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.

2) Отрезки соединяющие центр вписанной окружности с точками касания, перпендикулярны сторонам треугольника (как радиусы, проведенные в точку касания):

3) Вписанная в треугольник окружность делит стороны треугольника на 3 пары равных отрезков.

(как отрезки касательных, проведенные из одной точки).

Видео:Окружность с центром O вписанная в прямоугольный треугольник ЕГЭСкачать

Окружность, вписанная в треугольник

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Определение окружности, вписанной в треугольник

Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).

Окружность с центром о вписанная в треугольник касается стороны

Можно дать и другое определение окружности, вписанной в треугольник.

Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.

При этом треугольник называется треугольником описанным около окружности . Центр вписанной в треугольник окружности явлется точка пересечения биссектрис треугольника. Центр окружности вписанной в треугольник называется инцентром треугольника.

Видео:Геометрия Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВСкачать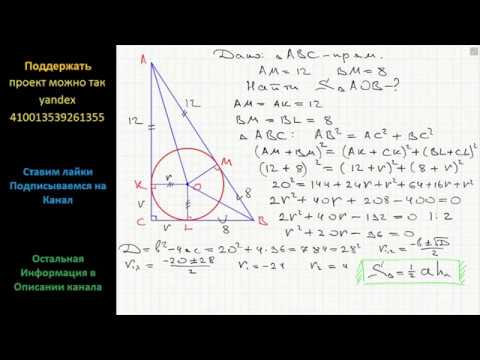

Теорема об окружности, вписанной в треугольник

Теорема 1. В любой треугольник можно вписать окружность.

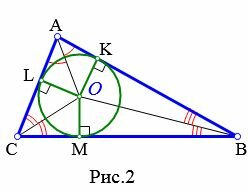
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.

Замечание 1. В любой треугольник можно вписать только одну окружность.

Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.