Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,044
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Окружность с центром о вписана в равнобедренную трапецию abcd
Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC = 1.
а) Треугольник AOH равнобедренный и трапеция ABCD равнобедренная, поэтому ∠AHO = ∠OAH = ∠CDA. Значит, прямые OH и CD параллельны, а так как OQ — средняя линия трапеции, то параллельны прямые OQ и AD. Противоположные стороны четырёхугольника DQOH попарно параллельны, следовательно, DQOH — параллелограмм.
б) Пусть окружность с центром в точке O радиуса R касается стороны CD в точке P. В прямоугольных треугольниках OPQ и AHB имеем
Пусть AH = x. Поскольку трапеция ABCD равнобедренная, AD = 2AH + BC; DH = AH + BC = x + 1. Тогда
откуда x = 1. Значит, AD = 2x + 1 = 3.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Вписанная в равнобедренную трапецию окружностьКакими свойствами обладает вписанная в равнобедренную трапецию окружность? 1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность. Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
|
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
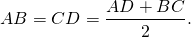
Если MN —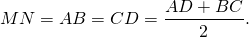
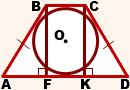По свойству равнобедренной трапеции,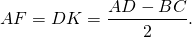
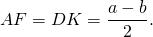
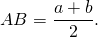
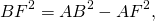
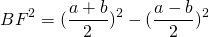
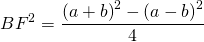
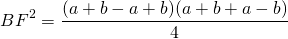
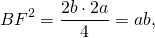
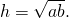
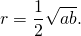
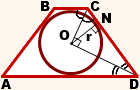Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,