Окружность с центром о касается сторон ab bc ac

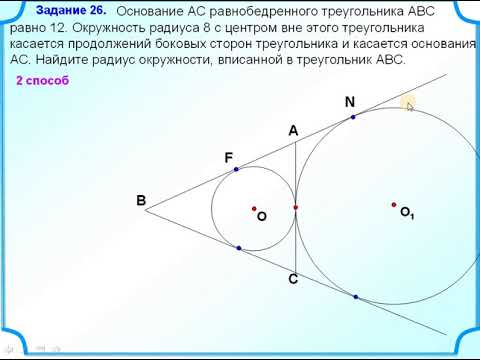
Задание 16. Окружность с центром О, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках С1, В1 и А1 соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника АВ1С1.

а) Докажите, что C1Q — биссектриса угла AC1B1.

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник AB1C1 если известно что ВС = 7, АВ = 15, АС = 20.

а) В треугольник ABC вписана окружность с центром в точке O. Стороны AB и AC – касательные к окружности и по теореме об отрезках касательных AC1=AB1 и, следовательно, треугольник AC1B1 – равнобедренный. AQ – биссектриса угла A по условию и в равнобедренном треугольнике AC1B1 биссектриса AA2 (продолжение AQ) является медианой и высотой. Следовательно, QA2 в треугольнике C1QB1 является также медианой и высотой, а сам треугольник C1QB1 – равнобедренный, так как .

По теореме об угле между касательной (AC1) и хордой (C1B1), имеем:

,

следовательно, C1Q – биссектриса угла AC1B1.

б) Рассмотрим треугольник AC1B1. Известно, что центр вписанной окружности находится в точке пересечения биссектрис углов, поэтому для AC1B1 центр вписанной окружности соответствует точке Q.

Найдем расстояние от точки O до точки Q, равный радиусу r вписанной окружности в треугольник ABC. Используя формулу площади треугольника ABC, можно записать

,

где p – полупериметр треугольника ABC. То есть, радиус r, равен:

Площадь треугольника ABC также можно найти по формуле Герона:

,

где a, b, c – стороны треугольника ABC.

Делаем вычисления. Полупериметр треугольника ABC, равен:

,

площадь треугольника ABC, равна:

и радиус вписанной окружности

,

Видео:🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно?

Геометрия | 5 — 9 классы

Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно.

Найдите дугу MK, дугу MN, дугу NK, если угол АВС = 62 градусам, угол АСВ = 68 градусам.

В ΔАВС ∠А = 180° — (62° + 68°) = 180° — 130° = 50°.

Радиус проведенный в точку касания, перпендикулярен касательной.

Сумма углов четырехугольника равна 360°.

В четырехугольнике АМОК :

∠М + ∠К = 90° + 90° = 180°, значит

∠МОК = 180° — 50° = 130°,

этот угол центральный, значит и градусная мера дуги МК равна 130° :

∠MON = 180° — ∠B = 180° — 62° = 118°, ⇒

∠NOK = 180° — ∠C = 180° — 68° = 112°, ⇒

Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

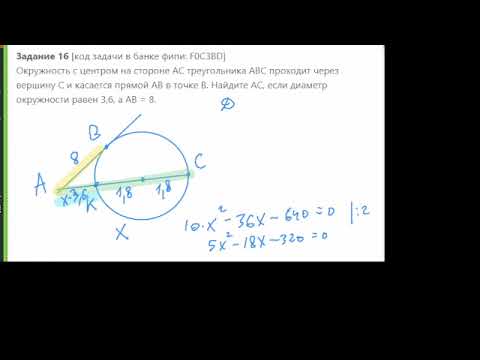
Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2?

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2.

Найди углы треугольника ОАВ.

Видео:Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2?

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2.

Найди углы треугольника ОАВ.

Видео:№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

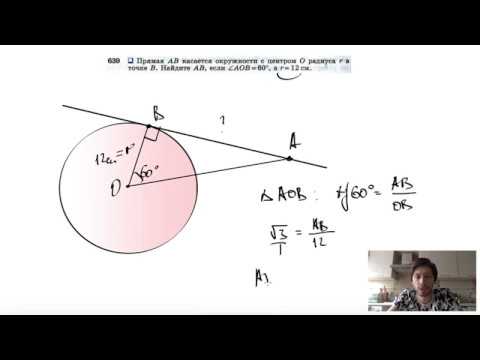
Окружность с центром в точке О касается сторон АВ, ВС и АС треугольника АВС в точках Р, К, Т соотв?

Окружность с центром в точке О касается сторон АВ, ВС и АС треугольника АВС в точках Р, К, Т соотв.

Нужно найти градусные меры дуг РК, КТ, ТР и угол РКТ, если угол АВС = 57, и если угол ВАС = 95.

Видео:Окружность с центром в точке O описана ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Окружность в центре О касается сторон АВ, ВС, АС ΔАВС, в точках M, N, K соответственно?

Окружность в центре О касается сторон АВ, ВС, АС ΔАВС, в точках M, N, K соответственно.

Угол АВС = 62, угол АСВ = 68 Найти : дугу MN.

Дугу MK, дугу NK, углы треугольника MNK.

Видео:2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

Точки а, b?

C лежат на окружности с центром О , угол АОС = 120 градусов , дуги АВ : ВС = 3 : 5 .

Найдите углы треугольника АВС.

Видео:Окружность касается боковых сторон АВ и ВС остроугольного треугольника АВС в точкахА и С соответствеСкачать

Окружность с центром о касается сторон ав, вс, ас треугольника авс в точках м, n, k найти дугу nm, mk, nk, если угол авс равен 62, а угол асв 68?

Окружность с центром о касается сторон ав, вс, ас треугольника авс в точках м, n, k найти дугу nm, mk, nk, если угол авс равен 62, а угол асв 68.

Видео:2184 касательная в точках A и B к окружности с центром О пересекаютсяСкачать

Точки А В С лежат на окружности угол В = 60′ дуга АВ относиться к дуге ВС также как 7 : 5 Найти углы треугольника АВС?

Точки А В С лежат на окружности угол В = 60′ дуга АВ относиться к дуге ВС также как 7 : 5 Найти углы треугольника АВС.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Точки А, В, С лежат на окружности с центром О?

Точки А, В, С лежат на окружности с центром О.

Угол АОВ = 80 градусов, дуга АС : на дугу ВС — 2 : 3.

Найдите углы треугольника АВС.

Видео:Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Точки А, В, С лежат на окружности с центром О, угол АОВ равен 80 градусов, дуга АВ относится к дуге ВС, как 2 относится к 3, Найдите углы треугольника АВС?

Точки А, В, С лежат на окружности с центром О, угол АОВ равен 80 градусов, дуга АВ относится к дуге ВС, как 2 относится к 3, Найдите углы треугольника АВС.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Треугольник АВС вписан в окружность, угол АВС равен 60 градусов?

Треугольник АВС вписан в окружность, угол АВС равен 60 градусов.

Найдите величину дуги АВ, если дуга АВ равна двум дугам ВС.

На этой странице сайта вы найдете ответы на вопрос Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций ..

Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона.

Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8.

1) вектор а = 2i — j 2) координаты вектора c .

Вот, пожалуйста✩ ^ _ ^ Все очень просто решается по теореме Пифагора.

Решение задания приложено.

ВС = MB — MC = 18, 2 — 9, 4 = 8, 8 Ответ : 1.

1). треугольники КВА = КАD по 2 — ум сторонам и углу между ними, т. К. АD = АВ (ABCD ромб), КА — общая, углы КАВ = КАD. 2) Из равенства треугольников следует что КВ = КD.

3 и 4 не могут существовать, т. К у треугольника сумма любых двух сторон должна быть больше третьей.

Примем коэффициент подобия стороны треугольника за — х, значит : ▪одна сторона — 4х ▪ вторая сторона — 6х ▪ третья сторона — 7х ▪периметр треугольника это сумма всех его сторон, а т. К. тругольники подобные, значит стороны одного треуг. Соответстве..

Видео:В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задание 16. Математика ЕГЭ. Окружность с центром О, вписанная в треугольник АВС, касается его сторон АВ, АС и ВС в точках С1, В1 и А1 соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника АВ1С1.

Задание. Окружность с центром О, вписанная в треугольник АВС, касается его сторон АВ, АС и ВС в точках С₁, В₁ и А₁ соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника АВ₁С₁.

а) Докажите, что С₁Q – биссектриса угла АС₁В₁.

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник АС₁В₁, если известно, что ВС = 15, АВ = 13, АС = 14.

Решение:

Угол ∠QB₁C₁ – вписанный в окружность угол, он равен половине дуги, на которую он опирается, т. е.

Так как АВ – касательная к окружности и QC₁ – хорда окружности, то угол между хордой и касательной окружности, проведенной через конец хорды, равен половине дуги, лежащей внутри этого угла, т. е.

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник АС₁В₁, если известно, что ВС = 15, АВ = 13, АС = 14.

Так как AQ и C₁Q – биссектрисы треугольника ∆AB₁C₁, тогда точка пересечения биссектрис Q – центр вписанной в треугольник ∆AB₁C₁ окружности. Точка Q – точка пересечения биссектрисы AQ и окружности с центром О, то расстоянием от точки О до точки Q – центра окружности, вписанной в треугольник ∆AB₁C₁ является OQ – радиус окружности с центром О, вписанный в треугольник ∆АВС.

P = 13 + 15 + 14 = 42

Площадь треугольника ∆АВС найдем по формуле Герона:

📹 Видео

№643. Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, еслиСкачать

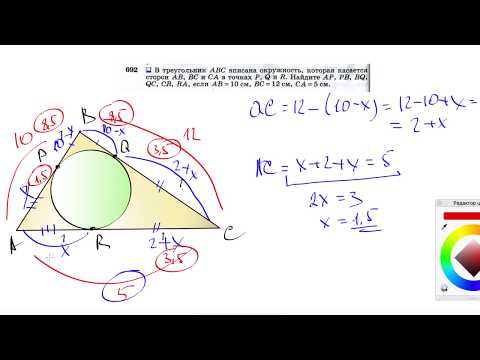
№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

🔴 В угол C, равный 79°, вписана окружность ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°.ОГЭ МатематикаСкачать

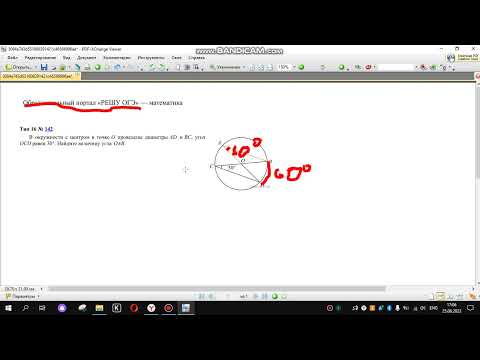
ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать