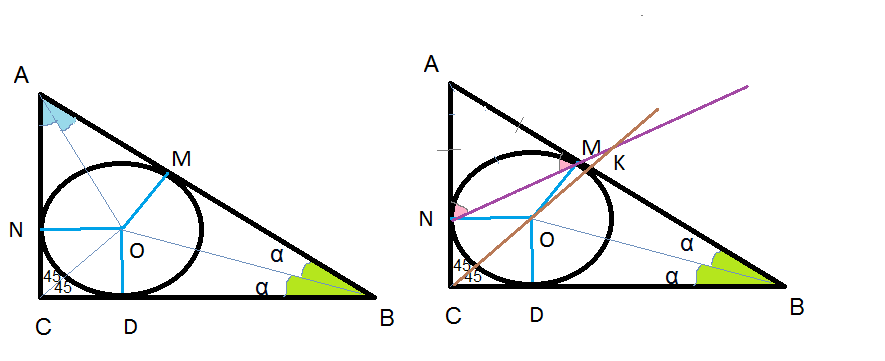
Условие
окружность с центром о, вписанная в прямоугольный треугольник АВС, касается гипотенузы АВ в точке М, а катета АС — в точке N, АС
Решение
O- точка пересечения биссектрис СО; ВО и АО.
∠ NCO=∠ DCO=45^(o);
∠ NBO=∠ DBO;
Обозначим α =∠ NBO=∠ DBO
В треугольнике АВС
∠ B=2*α ; ∠ A=90^(o)-2*α
По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны.
Значит, AN=AM
Δ AMN — равнобедренный
∠ CNM — смежный с углом ∠ ANM
∠ СNM= 180^(o) — ∠ ANM= 180^(o)-(45^(o)+α )=135^(o)- α
В Δ NKC:
∠ СNM=135^(o)- α
∠ NCO=45^(o);
Значит ∠ СKN= 180^(o) — ∠ СNM — ∠ NCO= 180^(o) — (135^(o)- α )-45^(o)= α
∠ СKN= α =(1/2) ∠ АВС
Видео:Геометрия Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВСкачать
Окружность с центром 0 вписанная в прямоугольный треугольник авс
Окружность с центром О, вписанная в прямоугольный треугольник АВС, касается гипотенузы АВ в точке М, а катета АС — в точке N, AC
Мы использовали теорему о внешнем угле и то факт, что центр вписанной окружности лежит на точке пересечения биссектрис. Что и требовалось доказать.
б) Из пункта а) заключаем, что углы OBM и OKM равны, следовательно, точки O, B, K, M лежат на одной окружности. Углы OMB и OKВ — прямые, поскольку центр вписанной окружности лежит на биссектрисе угла. Тогда треугольник CKB является равнобедренным с прямым углом CKB, откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | 3 |
| Получен обоснованный ответ в пункте б имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:№16 Профильный ЕГЭ. Окружность с центром О, вписанная в прямоугольный треугольник ABC касаетсяСкачать  Окружность с центром 0 вписанная в прямоугольный треугольник авсЗадание 16. Окружность с центром О, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках С1, В1 и А1 соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника АВ1С1. а) Докажите, что C1Q — биссектриса угла AC1B1. б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник AB1C1 если известно что ВС = 7, АВ = 15, АС = 20. а) В треугольник ABC вписана окружность с центром в точке O. Стороны AB и AC – касательные к окружности и по теореме об отрезках касательных AC1=AB1 и, следовательно, треугольник AC1B1 – равнобедренный. AQ – биссектриса угла A по условию и в равнобедренном треугольнике AC1B1 биссектриса AA2 (продолжение AQ) является медианой и высотой. Следовательно, QA2 в треугольнике C1QB1 является также медианой и высотой, а сам треугольник C1QB1 – равнобедренный, так как По теореме об угле между касательной (AC1) и хордой (C1B1), имеем:
следовательно, C1Q – биссектриса угла AC1B1. б) Рассмотрим треугольник AC1B1. Известно, что центр вписанной окружности находится в точке пересечения биссектрис углов, поэтому для AC1B1 центр вписанной окружности соответствует точке Q. Найдем расстояние от точки O до точки Q, равный радиусу r вписанной окружности в треугольник ABC. Используя формулу площади треугольника ABC, можно записать
где p – полупериметр треугольника ABC. То есть, радиус r, равен: Площадь треугольника ABC также можно найти по формуле Герона:
где a, b, c – стороны треугольника ABC. Делаем вычисления. Полупериметр треугольника ABC, равен:
площадь треугольника ABC, равна: и радиус вписанной окружности
📹 ВидеоОкружность вписанная в треугольник и описанная около треугольника.Скачать  №694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать  №705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать  ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать  Окружность с центром O вписанная в прямоугольный треугольник ЕГЭСкачать  Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать  Окружность, вписанная в прямоугольный треугольник | Геометрия 8-9 классыСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать  Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать  ЕГЭ Задание 16 Вписанная окружность Теорема косинусовСкачать  Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать  Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать  Треугольник и окружность #shortsСкачать  ВПИСАННАЯ ОКРУЖНОСТЬ + ПРАВИЛА ОФОРМЛЕНИЯ!Скачать  Геометрия Центр окружности, вписанной в прямоугольный треугольник удален от концов гипотенузы на aСкачать  ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать  Задание 24 Описанный прямоугольный треугольникСкачать  |
 .
.
 ,
, ,
,
 ,
, ,
,
 ,
,