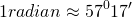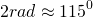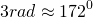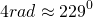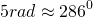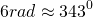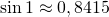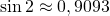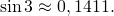Лучший способ запомнить новую информацию в математике – это понять логику. Поэтому в этой статье я расскажу вам логику тригонометрического круга.
На нем есть (16) стандартных точек. В них можно отметить числа с пи , можно градусы (имеется в виду градусные меры углов).

На круге каждой точке соответствует бесконечное множество чисел и градусов, поэтому запомнить их все невозможно. Гораздо лучше понять как расположены числа и градусы (для этого вы можете прочесть статьи здесь и здесь ).
Дальше я сосредоточусь на том, как запомнить расположение чисел на осях синуса, косинуса, тангенса и котангенса.
- Как запомнить какой точке какой синус и косинус соответствует?
- — косинус равен абсциссе точки на числовой окружности — синус равен ординате точки на числовой окружности.
- Синусы углов и как их сравнивать: описание формул, примеры и решение
- Содержание:
- Как сравнивать синусы углов – sin острого угла и пример расчета
- Синус произвольного угла – определение, пример
- Как сравнить синусы углов – анализ значений
- Узнать ещё
- Синус 1, sin 2, sin 3
- 📺 Видео
Видео:ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Как запомнить какой точке какой синус и косинус соответствует?
Шаг 1. Прежде всего, вспомните, что обычно горизонтальную ось называют осью косинусов, а вертикальную — осью синусов, так как:
— косинус равен абсциссе точки на числовой окружности
— синус равен ординате точки на числовой окружности.
Поэтому положительные значения косинусов и синусов расположены там же, где соответственно «иксы» и «игреки» положительны. Аналогично с отрицательными (на картинке ниже: оранжевые – плюс, синие – минус).
Шаг 2. Вспомните, что радиус тригонометрического круга равен (1), а это значит, что единицы и минус единицы на осях будут там, где круг пересечет оси.
Шаг 3. Так как ось котангенсов — это скопированная ось косинусов сдвинутая на 1 вверх, то и положительные отрицательные части осей там же где и на оси косинусов. Аналогично с осью тангенсов и синусов.
Шаг 4. Значение «(1)» на оси тангенсов и котангенсов находятся на одном уровне с единицей на оси косинусов и синусов. Аналогично, (-1) находятся на одном уровне с (-1) на оси синусов и косинусов.
Шаг 5. Дальше стоит понять, что (±frac<sqrt>) находится ближе к (0), чем (±sqrt).
Шаг 6. (±sqrt) – это самые крайние точки, которые мы ставим на осях.
Опять же, подписывать все значения на тригонометрическом круге, и расставлять все числа на осях ни к чему. Достаточно нанести лишь те значения, которые надо найти.
Пример (ЕГЭ). Найдите значение выражения (36sqrt, tg,frac sin,frac).
Решение:
Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Синусы углов и как их сравнивать: описание формул, примеры и решение
Содержание:
Одним из видов тригонометрических функций является синус. Данная функция рассчитывается для любых углов, находящихся в окружности. Прямоугольный треугольник применяется для определения значения sin острых углов. Если угол имеет обозначение Х, алгебра предполагает использование выражения sinХ. Перед тем, как сравнивать синусы, необходимо определить тип угла, создать окружность, установить четверть этой окружности.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Как сравнивать синусы углов – sin острого угла и пример расчета
Острый угол – угол меньше 90 градусов. Для расчета синуса необходимо рассчитать соотношение противолежащих сторон. Сравнивается катет с гипотенузой.
Катет представляет собой одну из сторон в прямоугольном треугольнике. Обязательное условие – прямой угол относительно противоположенному ребру фигуры. Данный предмет называется гипотенузой. Если фигура не относится к прямоугольным треугольникам, катеты отсутствуют. Рассмотрим на примере расчет синуса острых углов:
Задание: В прямоугольном треугольнике длина гипотенузы составляет 5 сантиметров. Длина катета – 3 см. Необходимо рассчитать значение синуса угла, противоположенного катету.
Как решить: Теория указывает, что для выявления синуса рассчитывается отношение противоположенной стороны и гипотенузы, следовательно:
sin propto = 35 sin f_0 ^ propto = 35
Итог: sin propto = 35
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Синус произвольного угла – определение, пример
Произвольный угол определяется ∝ ∝. Его образует ось ОхОх совместно с произвольным радиусом от вектора ОА. Данный вектор равен (ах; ау) ОА = (ах; ау). Это соотношение проекционного значения данной векторной величины между осью ОуОу, длиной а=ОА. Рассмотрим пример расчета sin произвольного угла:
Задача: Угол образует ось абсцисс а = (-1; 2) и вектор а = (-1; 2).
Для решения задачи используется установленное тригонометрическое уравнение:
sin sin propto = 2 (-1)_2 + 2_2 sqrt = 25 sqrt = 25 sqrt = 2 ( — 1 ) 2 + 22 = 25 = 255
Итог: sin = 25 sqrt 5
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Как сравнить синусы углов – анализ значений
Синусом называют функцию угла. Он находится в окружности, разделенной на 4 четверти. Для сравнения sin используется следующая таблица:
| Угол | Значение |
| 0 0 | Всегда = 0 |
| 30 0 | 0,5 |
| 60 0 | sqrt /2 approx 1, 7/2 approx 0,9 |
| 90 0 | 1 |
Важно запомнить: если угол находится в первой четверти, его sin будет возрастать до 90 градусов. Убывание значения отмечается во второй части окружности. Он стремится от 1 к 0. В третьей и четвертой четверти значение sin отрицательное. Для третьей части характерно стремление от нуля к -1, для 4 четверти – от -1 к 0.
Рассмотрим сравнение синусов на примерах:
- Нужно установить соотношение между sin 195° и sin 200° . Для этого используется окружность. Местоположение 195, 200 находится на этой окружности. Это свидетельствует о том, что sin 195° >sin 200° , так как расположен ниже.
- Определить отношение между sin 734° и sin -1066° .
Диаметр цельного круга составляет 360 градусов, двух окружностей – 720 градусов. Отсюда следует, что 734° включает два круга и 14 градусов. Если обойти три раза по кругу в обратную сторону, получится -360 х 3 = -1080 градусов. Получается, что точка -1066 – это три окружности и еще 14 градусов. Синусы точек с одинаковой градусной мерой равные. sin 734°= sin -1066°
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Узнать ещё
Знание — сила. Познавательная информация
Видео:Сравнение значений тригонометрических выраженийСкачать

Синус 1, sin 2, sin 3
Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.
Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.
Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.
Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здес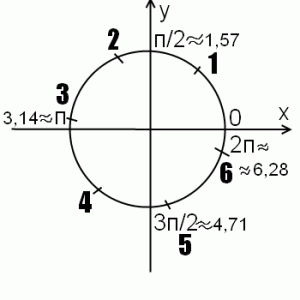
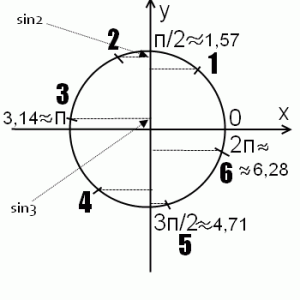
Соответственно внизу синус отрицателен: sin 4 sin4, ведь любое положительное число больше любого отрицательного.
Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.
Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:
Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:
Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.
📺 Видео
Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Вычисление значений тригонометрических функцийСкачать

Как искать точки на тригонометрической окружности.Скачать

18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Что больше ➜ sin4 или sin5 ➜ Супер способСкачать

Тригонометрическая окружность для непонимающихСкачать

Сравнение значений косинусов разных угловСкачать

Сравнение значений синусов разных угловСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Знаки синуса, косинуса, тангенса ЛекцияСкачать
Сравнение тангенсов разных угловСкачать

Формулы приведения - как их легко выучить!Скачать