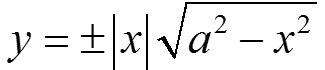Информация о задаче
Задача №2461 параграфа №1 главы №8 «Применения интеграла» книги Г.Н. Бермана «Сборник задач по курсу математического анализа» (22-е издание, 2002 год).
Условие задачи
Окружность [math]x^2+y^2=8[/math] разделена параболой [math]y=frac[/math] на две части. Найти площади обеих частей.
Решение
Найдём точки пересечения заданных линий:
Графики пересекаются в точках [math](-2;2)[/math] и [math](2;2)[/math] . Пусть [math]S_1[/math] – площадь области, расположенной внутри параболы, а [math]S_2[/math] – область вне параболы. Так как и парабола и окружность симметричны относительно оси ординат, то [math]S_1=2S_0[/math] , где [math]S_0[/math] – площадь области, расположенной внутри параболы справа от оси ординат.
Так как радиус окружности [math]R=sqrt[/math] , то:
[dmath] S_2= pi-S_1 =6pi-frac. [/dmath]
Площадь фигуры в декартовой системе координат. Примеры
Уравнение верхней и нижней границы:
Пример 2
В каком отношении парабола y 2 = 2 x делит площадь круга x 2 + y 2 = 8 ?
Точки пересечения: x 2 + 2 x – 8 = 0 → x 1 = –4, x 2 = 2 ( x > 0) .
Задание №4. Начала интегрального исчисления, простейшие дифференциальные уравнения, основы теории числовых и функциональных рядов
Задание №4. Начала интегрального исчисления, простейшие дифференциальные уравнения, основы теории числовых и функциональных рядов.
I. Вычисление неопределенных интегралов
I.1. Применение основной таблицы интегралов. Вычислить интегралы:
1. 
; 2. 
; 3. 
; 4. 
;
5. 
; 6. 
; 7. 
8. 
;
9. 
; 10. 
I.2. Замена переменных в неопределенном интеграле. Вычислить интегралы:
1. 
; 2. 
; 3. 
; 4. 
;
5. 
; 6. 
; 7. 
; 8. 
;
9. 
; 10. 
; 11. 
; 12. 
; 13. 
;
14. 
; 15. 
; 16. 
.
I.3. Интегрирование по частям. Вычислить интегралы:
1. 
; 2. 
; 3. 
; 4. 
; 5. 
;
6. 
; 7. 
; 8. 
; 9. 
; 10. 
I.4. Интегрирование рациональных функций:
1. 
; 2. 
; 3. 
; 4. 
;
5. 
; 6. 
; 7. 
; 8) 
; 9) 
;
10) 
; 11) 
; 12) 
I.5. Интегрирование иррациональных функций:
1. 
; 2) 
; 3) 
; 4) 
;
5) 
; 6) 
I.6. Интегрирование тригонометрических функций:
1. 
; 2) 
; 3) 
; 4) 
; 5) 
;
6) 
; 7) 
; 8) 
; 9) 
;
10) 
I.7. Интегрирование показательных и логарифмических функций:
1) 
; 2) 
; 3) 
; 4) 
; 5) 
6) 
; 7) 
; 8) 
II. Вычисление определенных интегралов.
II.1. Применение формулы Ньютона-Лейбница:
1) 
; 2) 
; 3) 
; 4) 
; 5) 
;
6) 
; 7) 
; 8) 
; 9) 
; 10) 
;
11) 
; 12) 
II.2. Замена переменной в определенном интеграле:
1) 
; 2) 
; 3) 
; 4) 
; 5) 
;
6) 
; 7) 
; 8) 
II.3. Средние значения функций.
Вычислить среднее значение функций в заданном сегменте:
1) 
в сегменте [1;4].
2) 
в сегменте [1;1,5].
3) 
и 
в сегменте [0;π].
4) Найти наибольшее и наименьшее значения функции
в сегменте [-1;1]
II.4. Вычисление площадей плоских фигур.
1). Вычислить площадь фигуры, ограниченной кривыми 
и 
.
2). Окружность 
разделена параболой 
на две части. Найти площади обеих частей.
3). Найти площадь фигуры, ограниченной дугой гиперболы и ее хордой, проведенной из фокуса перпендикулярно к действительной оси.
4). Вычислить площадь криволинейной трапеции с основанием [a;b], ограниченной линией 
.
5) Найти площадь фигуры, ограниченной замкнутой линией 
.
II.5. Вычисление длины дуги кривой.
1) Найти длину дуги линии 
от 
до 
.
2) Найти периметр одного из криволинейных треугольников, ограниченных осью абсцисс и линиями 
и 
.
3) На циклоиде 
найти точку, которая делит первую арку циклоиды по длине в отношении 1:3.
II.6. Вычисление площадей поверхностей и объемов тел вращения.
1) Вычислить площадь поверхности вращения параболы 
вокруг оси абсцисс от вершины до точки с абсциссой 
.
2) Вычислить площадь поверхности, образованной вращением одной арки синусоиды (от 0 до π) вокруг оси абсцисс.
3) Фигура, ограниченная гиперболой 
и прямой 
(h>0), вращается вокруг оси абсцисс. Найти объем тела вращения.
4) Симметричный параболический сегмент с основанием а и высотой h вращается вокруг основания. Вычислить объем тела вращения, которое при этом получается («лимон Кавальери»).
III. Решение простейших дифференциальных уравнений.
III.1. Уравнения с разделяющимися переменными.
Найти общие решения уравнений:
1) 
; 2) 
; 3) 
; 4) 
;
5) 
; 6) 
Найти частные решения уравнений, удовлетворяющие начальным условиям:
7) 
; 8) 
III.2. Однородные уравнения.
Найти общие решения уравнений:
1) 
; 2) 
; 3) 
; 4) 
; 5) 
$
6) 
Найти частные решения уравнений, удовлетворяющие начальным условиям:
7) 
; 8) 
Ш.3. Линейные уравнения 1-го порядка.
Найти общие решения уравнений:
1) 
; 2) 
; 3) 
; 4) 
;
5) 
Найти частные решения уравнений, удовлетворяющие начальным условиям:
6) 
; 7) 
Ш.4. Уравнения 2-го порядка.
Найти общие решения уравнений:
1) 
; 2) 
; 3) 
; 4) 
; 5) 
;
6) 
Найти частные решения уравнений, удовлетворяющие начальным условиям:
7) 
; 8) 
Ш.5. Уравнения 2-го порядка с постоянными коэффициентами.
Найти общие решения уравнений:
1) 
; 2) 
Найти частные решения уравнений, удовлетворяющие начальным условиям:
3) 
; 4) 
IV. Числовые и функциональные ряды
1) 
; 2) 
IV.2. Исследовать на сходимость ряды:
1) 
; 2) 
; 3) 
IV.3. Доказать сходимость рядов с помощью признака Даламбера:
1) 
; 2) 
; 3) 
IV.4. Доказать сходимость рядов с помощью признака Коши:
1) 
; 2) 
IV.5. Абсолютная и условная сходимость рядов. Выяснить, какие из рядов сходятся абсолютно, какие — условно, какие — расходятся:
1) 
; 2) 
; 3) 
; 4) 
IV.6. Определить области сходимости функциональных рядов:
1) 
; 2) 
; 3) 
; 4) 
IV.7. Убедиться, что данные ряды равномерно сходятся на всей оси ОХ:
1) 1+
; 2) 
; 3) 
IV.8. Разложить функции в ряд Тейлора в окрестности указанных точек:
1) 
в окрестности точки х = 1;
2) 
в окрестности точки х = 2;
3) 
в окрестности точки х = 0;
4) 
в окрестности точки х = 0;
5) 
в окрестности точки х = 0;
6) 
в окрестности точки х = 0