Математика | 5 — 9 классы
Постройте окружность радиус равным 4 см проведите касательную к окружности .
Дайте основное свойство касательной .
Основное свойство косательной то , что она имеет только 1 общую точку с окружностью.
- Начертите и обозначьте окружность с центром N и радиусом 2 см?
- Постройте касательную к окружности, проходящую через данную точку вне этой окружности?
- Начертите произвольную окружность и отметьте на ней точку A ?
- К окружности с центром в точке O проведены касательная AB и секущая AO найдите радиус окружности если AB = 14см?
- Найдите радиус окружности, если расстояния от концов диаметра до касательной равны 4 см и 8 см?
- Из точки А проведены две касательные к окружности с центром в точке О?
- К окружности с центром в точке О проведены касательная АБ и секущая АО?
- К окружности проведены две касательные Какие углы образует с ними отрезок, соединяющий точки касания, если угол между касательными равен 85 градусов?
- Длина отрезка касательной , проведенной к окружности из точки а , равна 8, а растояние от точкиа до центра о окружности равно 10, найдите радиус окружности?
- Из точки окружности проведены касательная и хорда, отделяющая от окружности 80 градусов Найди угол между хордой и касательной?
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Практическая работа по теме «Прямая и окружность», 6 класс
- Просмотр содержимого документа «Практическая работа по теме «Прямая и окружность», 6 класс»
- 🎦 Видео
Видео:Школа для родителей. Циркуль, окружность, радиус, диаметр.Скачать

Начертите и обозначьте окружность с центром N и радиусом 2 см?
Начертите и обозначьте окружность с центром N и радиусом 2 см.
Постройте диаметр AB, хорды AC и BC, касательную к окружности в точке A.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Постройте касательную к окружности, проходящую через данную точку вне этой окружности?
Постройте касательную к окружности, проходящую через данную точку вне этой окружности.
Видео:Радиус и диаметрСкачать

Начертите произвольную окружность и отметьте на ней точку A ?
Начертите произвольную окружность и отметьте на ней точку A .
Постройте касательную к окружности в точке A.
Видео:Касательные к окружностиСкачать

К окружности с центром в точке O проведены касательная AB и секущая AO найдите радиус окружности если AB = 14см?
К окружности с центром в точке O проведены касательная AB и секущая AO найдите радиус окружности если AB = 14см.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите радиус окружности, если расстояния от концов диаметра до касательной равны 4 см и 8 см?
Найдите радиус окружности, если расстояния от концов диаметра до касательной равны 4 см и 8 см.
Видео:Геометрия Окружность радиуса 4 касается внешним образом второй окружности в точке B. ОбщаяСкачать

Из точки А проведены две касательные к окружности с центром в точке О?
Из точки А проведены две касательные к окружности с центром в точке О.
Найдите радиус окружности , если угол между касательными равен 60 градусов , а расстояние от точки А до тоски О равно 6.
Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

К окружности с центром в точке О проведены касательная АБ и секущая АО?
К окружности с центром в точке О проведены касательная АБ и секущая АО.
Найдите радиус окружности , если АБ = 65 , АО = 97.
Видео:Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

К окружности проведены две касательные Какие углы образует с ними отрезок, соединяющий точки касания, если угол между касательными равен 85 градусов?
К окружности проведены две касательные Какие углы образует с ними отрезок, соединяющий точки касания, если угол между касательными равен 85 градусов.
Видео:Построение касательной к окружностиСкачать

Длина отрезка касательной , проведенной к окружности из точки а , равна 8, а растояние от точкиа до центра о окружности равно 10, найдите радиус окружности?
Длина отрезка касательной , проведенной к окружности из точки а , равна 8, а растояние от точкиа до центра о окружности равно 10, найдите радиус окружности.
Видео:Что такое круг окружность радиусСкачать

Из точки окружности проведены касательная и хорда, отделяющая от окружности 80 градусов Найди угол между хордой и касательной?
Из точки окружности проведены касательная и хорда, отделяющая от окружности 80 градусов Найди угол между хордой и касательной.
Вы зашли на страницу вопроса Постройте окружность радиус равным 4 см проведите касательную к окружности ?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.
1, 10 ответ В — 3, решение в приложенном файле 1, 11 б — 16п 1, 12 в координата суммы вектора находится сложением координатсоответствующих векторов а( — 2 ; 3) в(3 ; 4) с = ( — 2 + 3 ; 3 + 4) = (1 ; 7).
Видео:5 класс, 22 урок, Окружность и кругСкачать

Касательная к окружности
О чем эта статья:
Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.























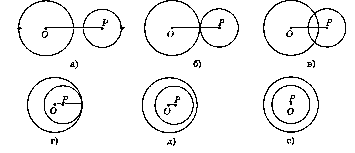 адание 1 (1 б.)
адание 1 (1 б.)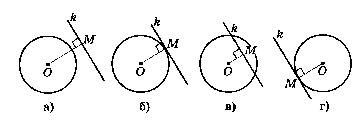 адание 2 (1 б.)
адание 2 (1 б.)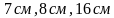 ; б)
; б) 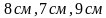 .
.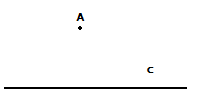 адание 6 (2 б.) Постройте равнобедренный треугольник с вершиной в точке А, основанием ВК, лежащим на прямой с, и боковыми сторонами равными 3 см.
адание 6 (2 б.) Постройте равнобедренный треугольник с вершиной в точке А, основанием ВК, лежащим на прямой с, и боковыми сторонами равными 3 см.