В остроугольном треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны;
б) Найдите отношение ЕН : АС, если угол АВС равен 30°.
Заметим, что отрезок AC виден из точек K и M под углом 90°, поэтому точки М, К, С и А лежат на одной окружности, диаметром которой является отрезок АС. Аналогично, точки M, K, H, E лежат на окружности, диаметром которой является MK.
Пусть Тогда
так как они опираются на одну дугу KC в окружности, описанной вокруг четырёхугольника AMKC. Кроме того,
так как они опираются на одну дугу KH в окружности, описанной вокруг четырёхугольника MKHE. Так как
прямые EH и АС параллельны, поскольку это соответственные углы при пересечении EH и AC секущей OA. Это и требовалось доказать.
б) Используем подобие треугольников:
кроме того,
поэтому
тогда EH =
Тем самым искомое отношение длин сторон равно 3:4.
Приведем другое решение пункта б).
Пусть КС = 2x, тогда из треугольника KHC находим HC = X, из ΔOKC: ∠KOC = 30°, тогда OC = 4x, откуда
В силу подобия ΔOEH и ΔОАС получаем:
Приведем решение Александра Шевкина (Москва).
а) Построим вспомогательную окружность с диаметром MK. Она пройдёт через точки E и H, так как
Построим вспомогательную окружность с диаметром AC. Она пройдёт через точки M и K, т. к.
По свойству вписанных углов а
значит,
А это соответственные углы при прямых ЕН и АС и секущей AE. Из равенства этих углов следует параллельность прямых ЕН и АС, что и требовалось доказать.
б) Прямая MK, проходящая через основания высот треугольника ABC, отсекает треугольник KMB, подобный треугольнику ABC. Коэффициент подобия равен
Рассмотрим треугольники MOK и EOH. Они подобны по двум углам: (свойство вписанных углов),
(вертикальные). Коэффициент подобия равен
Умножив полученные равенства
и
найдём отношение оно равно
Ответ:
Приведем решение Софии Николенко (Москва).
а) Пусть высоты АК и СМ пересекаются в точке О. Рассмотрим треугольник AMO. В нем ME является высотой, проведенной к гипотенузе, поэтому треугольники AME и OME подобны, а углы MAE и OME равны. Пусть эти углы равны α, тогда ∠MOE = 90° − α. Углы KOH и MOE равны 90° − α, тогда угол OKH равен α. Углы EMO и OKH равны так как опираются на одну дугу EH, таким образом, четырехугольник EMKH можно вписать в окружность.
Четырехугольник AMKC также можно вписать в окружность с диаметром AC. Углы KAC и KMC равны, углы KEH и KMC тоже равны, поэтому угол KEH равен углу KAC. Углы KEH и KAC являются соответственными при пересечении прямых EH и AC секущей AO. Таким образом, прямые EH и AC параллельны.
б) Рассмотрим треугольник AMO, пусть ME = x, тогда
Отсюда
Рассмотрим треугольник AME, в нем:
Треугольники AOC и EOH подобны по двум углам. Значит, откуда
Видео:Досрочный ОГЭ Математика. Задание 16.Скачать

Свойства высот треугольника. Ортоцентр
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если 

- Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
- Четырехугольник ВКМН также можно вписать в окружность.
- Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
- ,где R – радиус описанной окружности .
Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам
Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.
2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .
Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.
3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.
5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .
Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что
Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)
2. В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .
— смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).
Видео:Геометрия В треугольнике ABC проведена высота BD угол A = 60 угол C = 45 AB=10см Найдите сторону BCСкачать

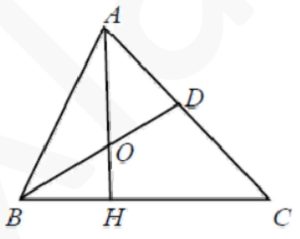
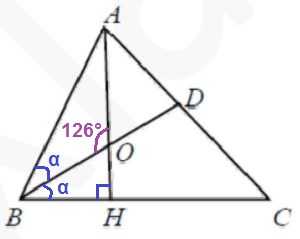
Решение №1391 В треугольнике АВС проведены высота АН и биссектриса BD, которые пересекаются в точке О.
В треугольнике АВС проведены высота АН и биссектриса BD, которые пересекаются в точке О. Найдите угол АВС, если ∠AOB = 126º.
Источник задания: alexlarin.net
Обозначим равные углы, образованные при делении угла В биссектрисой ВD, за α . Угол АНВ = 90°, т.к. АН – высота.
∠АОВ и ∠ВОН смежные их сумма равна 180°. Найдём ∠ВОН:
∠ВОН = 180º – ∠АОВ = 180º – 126º = 54º
Сумма углов ΔОВН равна 180°, найдём α:
α = 180º – (∠АНВ + ∠ВОН) = 180º – (90º + 54º) = 36º
Найдём ∠В:
∠В = α + α = 36 + 36 = 72°
Ответ: 72.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
💥 Видео
№532. В треугольнике ABC проведена высота ВН. Докажите, что если:Скачать

В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 2 и BC = BM. Найдите AHСкачать

16)В остроугольном треугольнике ABC проведена высота BH, угол BAC=48°. Найдите угол ABH. Ответ дайтеСкачать

Геометрия В прямоугольном треугольнике ABC проведена высота CH из вершины прямого углаСкачать

Геометрия Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружностиСкачать

В треугольнике ABC BM – медиана и BH – высота ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Геометрия Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружностиСкачать

№1042. В равностороннем треугольнике ABC со стороной а проведена высота BD. ВычислитеСкачать

ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

ОГЭ Задание 25 Подобные треугольникиСкачать
В остроугольном треугольнике ABC высота AH равна 9√69 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

15 задание ОГЭ по математике 2023 Треугольник Shorts #shorts #огэпоматематике2023 #треугольникСкачать

🔴 В треугольнике ABC проведена биссектриса ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать

#31. Регион ВсОШ 2023, 11.5Скачать

В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать