Вопрос по математике:
В окружности радиуса R=12 вписан правильный n-угольник. Определите его сторону и периметр если a)n=3 b)n=4 c)n=6
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- Как написать хороший ответ?
- Окружность радиуса 12 вписан правильный четырехугольник
- Задание 16. ЕГЭ. Четырёхугольник ABCD вписан в окружность радиуса R = 12.
- В окружность радиуса r вписан правильный
- В окружность радиуса r вписан правильный четырехугольник
- В окружность радиуса R вписан правильный четырехугольник?
- Найдите радиусы вписанной и описанной окружностей для правильного треугольника четырехугольника шестиугольника?
- Радиус окружности равен 6?
- Радиус окружности , описанной около правильного четырехугольника , равен 8 см ?
- 1. Радиус вписанного в треугольник окружности = r, найдите сторону треугольника 2?
- В правильный шестиугольник вписана окружность радиуса r?
- Радиус окружности равен 10см ?
- В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник?
- В окружность вписан правильный восьмиугольник?
- Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 8 см?
- Найдите площадь правильного 12 — тиугольника, вписанного в окружность радиуса 9?
- Правильный многоугольник
- Формулы, признаки и свойства правильного многоугольника
- Признаки правильного многоугольника
- Основные свойства правильного многоугольника
- Формулы правильного n-угольника
- Формулы длины стороны правильного n-угольника
- Формула стороны правильного n-угольника через радиус вписанной окружности
- Формула стороны правильного n-угольника через радиус описанной окружности
- Формулы радиуса вписанной окружности правильного n-угольника
- Формула радиуса вписанной окружности n-угольника через длину стороны
- Формула радиуса описанной окружности правильного n-угольника
- Формула радиуса описанной окружности n-угольника через длину стороны
- Формулы площади правильного n-угольника
- Формула площади n-угольника через длину стороны
- Формула площади n-угольника через радиус вписанной окружности
- Формула площади n-угольника через радиус описанной окружности
- Формула периметра правильного многоугольника
- Формула периметра правильного n-угольника
- Формула определения угла между сторонами правильного многоугольника
- Формула угла между сторонами правильного n-угольника
- Правильный треугольник
- Формулы правильного треугольника
- Формула стороны правильного треугольника через радиус вписанной окружности
- Формула стороны правильного треугольника через радиус описанной окружности
- Формула площади правильного треугольника через длину стороны
- Формула площади правильного треугольника через радиус вписанной окружности
- Формула площади правильного треугольника через радиус описанной окружности
- Углы между сторонами правильного треугольника
- Правильный четырехугольник
- Формулы правильного четырехугольника
- Формула стороны правильного четырехугольника через радиус вписанной окружности
- Формула стороны правильного четырехугольника через радиус описанной окружности
- Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
- Формула радиуса описанной окружности правильного четырехугольника через длину стороны
- Формула площади правильного четырехугольника через длину стороны
- Формула площади правильного четырехугольника через радиус вписанной окружности
- Формула площади правильного четырехугольника через радиус описанной окружности
- Углы между сторонами правильного четырехугольника
- Правильный шестиугольник
- Формулы правильного шестиугольник
- Формула стороны правильного шестиугольника через радиус вписанной окружности
- Формула стороны правильного шестиугольника через радиус описанной окружности
- Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
- Формула радиуса описанной окружности правильного шестиугольника через длину стороны
- Формула площади правильного шестиугольника через длину стороны
- Формула площади правильного шестиугольника через радиус вписанной окружности
- Формула площади правильного шестиугольника через радиус описанной окружности
- Углы между сторонами правильного шестиугольника
- Правильный восьмиугольник
- Четырехугольник, вписанный в окружность — основные свойства, признаки и формулы
- Общие сведения
- Основные правила
- Свойства и утверждения
- Формулы и соотношения
- Периметр и полупериметр
- Понятие площади
- Диагонали и углы
- Параметры для окружности
- В круг радиуса R вписан правильный треугольник. В круг наудачу брошена точка. Найти вероятность того, что эта точка окажется внутри треугольника
- Ваш ответ
- решение вопроса
- Похожие вопросы
- В окружность радиуса r вписан правильный
- Как написать хороший ответ?
- Контрольная работа по геометрии 9 класс, по теме «Правильные многоугольники».
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- В окружность радиуса 12 см вписан правильный треугольник. Вычислите: а) высоту треугольника; б) расстояние от центра окружности цо прямой, содержащей
- Ваш ответ
- решение вопроса
- Похожие вопросы
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
Окружность радиуса 12 вписан правильный четырехугольник
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

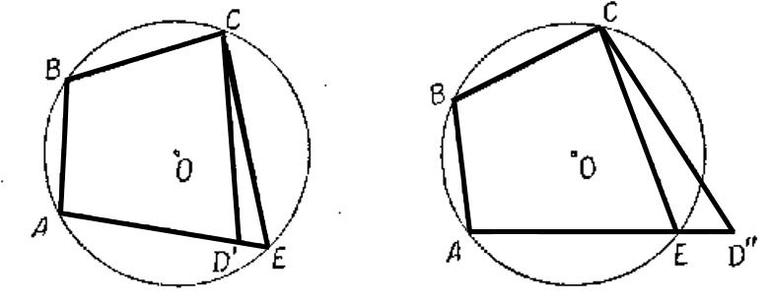
Задание 16. ЕГЭ. Четырёхугольник ABCD вписан в окружность радиуса R = 12.
Задание. Четырёхугольник ABCD вписан в окружность радиуса R = 12.
Известно, что AB = BC = CD = 18.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD.
Решение:
а) Докажите, что прямые BC и AD параллельны.
Проведем диагональ АС в четырёхугольнике ABCD.
Так как хорды AB = CD, то равны дуги ᴗAB = ᴗCD.
Угол ∠BCA – вписанный в окружность угол, который опирается на дугу ᴗAB.
Угол ∠CAD – вписанный в окружность угол, который опирается на дугу ᴗCD.
Значит, ∠BCA = ∠CAD – накрест лежащие углы при прямых BC и AD, AC – секущей.
Следовательно, прямые BC и AD параллельны.
б) Найдите AD.
Так как АВ = ВС, то треугольник ΔАВС – равнобедренный, следовательно, ∠BCA = ∠ВAС = α.
Углы ∠BCA = ∠CAD – накрест лежащие углы, тогда ∠ВAD = ∠BAC + ∠CAD = 2α.
Четырёхугольник ABCD – равнобедренная трапеция, значит, ∠CDA = ∠BAD = 2α.
Около треугольника ΔАВС описана окружность, тогда по теореме синусов имеет место равенство:
Используя основное тригонометрическое тождество, получим
Из треугольника ΔACD по теореме синусов найдем АС:
Пусть AD = x, тогда из треугольника ΔACD по теореме косинусов:
Если x = 18, то четырёхугольник ABCD вписанный в окружность является квадратом (по условию ABCD – трапеция). В этом случае радиус окружности равен R = 9√2, а это противоречит условию задачи (R = 12).
Следовательно, AD = 13,5.
Ответ: 13,5
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

В окружность радиуса r вписан правильный
Видео:Длина окружности. Математика 6 класс.Скачать

В окружность радиуса r вписан правильный четырехугольник
Видео:Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.Скачать

В окружность радиуса R вписан правильный четырехугольник?
Геометрия | 5 — 9 классы
В окружность радиуса R вписан правильный четырехугольник.
Найдите его площадь.
Правильный четырехугольник — это квадрат, значит в окружность вписан квадрат.
Диагональ квадрата является диаметром окружности.
Диагонали квадрата пересекаются пол прямым углом и делят квадрат на 4 равных прямоугольных треугольника, катеты которых раны радиусу описанной около квадрата окружности, т.
Тогда площадь квадрата равна площади 4 треугольников.
S = 4 * 1 / 2 * R * R = 2$R^ $.
Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Найдите радиусы вписанной и описанной окружностей для правильного треугольника четырехугольника шестиугольника?
Найдите радиусы вписанной и описанной окружностей для правильного треугольника четырехугольника шестиугольника.
Пожалуйста нужно срочно.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Радиус окружности равен 6?
Радиус окружности равен 6.
Найдите площадь правильного треугольника, вписанного в эту окружность.
Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Радиус окружности , описанной около правильного четырехугольника , равен 8 см ?
Радиус окружности , описанной около правильного четырехугольника , равен 8 см .
Найдите отношение периметра данного четырехугольника к длине вписанной окружности.
Видео:Построение 12 угольника циркулемСкачать

1. Радиус вписанного в треугольник окружности = r, найдите сторону треугольника 2?
1. Радиус вписанного в треугольник окружности = r, найдите сторону треугольника 2.
Радиус вписанный в правильный четырехугольник = r найдите сторону четырехугольника.
Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать
![ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]](https://i.ytimg.com/vi/YKbgCquokWg/0.jpg)
В правильный шестиугольник вписана окружность радиуса r?
В правильный шестиугольник вписана окружность радиуса r.
Найдите площадь шестиугольника.
Видео:Геометрия В окружность, диаметр которой равен v12, вписан правильный треугольник. На его высоте какСкачать

Радиус окружности равен 10см ?
Радиус окружности равен 10см .
Найдите стороны вписанного в окружность правильного треугольника , правильного четырехугольника , правильного шестиугольника .
Пожалуйста с решениеи .
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник?
В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник.
Найдите отношения периметров и площадей этих четырехугольников.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

В окружность вписан правильный восьмиугольник?
В окружность вписан правильный восьмиугольник.
Сумма длин всех его диагоналей, имеющих наименьшую длину, равна 8.
Найдите площадь правильного четырехугольника, вписанного в эту же окружность.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 8 см?
Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 8 см.
Видео:№ 101-200 - Геометрия 9 класс Мерзляк Рабочая тетрадьСкачать

Найдите площадь правильного 12 — тиугольника, вписанного в окружность радиуса 9?
Найдите площадь правильного 12 — тиугольника, вписанного в окружность радиуса 9.
Вопрос В окружность радиуса R вписан правильный четырехугольник?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. В подобных треугольниках и медианы (соответственные) подобны, и радиусы вписанных (описанных) окружностей подобны.
Все видно на рисунке. Угол АОВ разделили на 4 равных части. (биссектрисы делят углы пополам). Значит.
1) 4 + 3 + 2 = 9 2) 9х = 45 х = 5 5 * 2 = 10(см).
4 + 3 + 2 = 9частей 45 : 9 = 5 это равна одна часть Меньшая сторона равна 2 * 5 = 10.
1) б, т. К. 30 * 2 = 60 2) в, т. К. 120 / 2 = 60 3) б, т. К. 90 — 55 = 35 4) а 5) в, т. К. 180 — 140 = 40.
Вектора перпендикулярны, если их скалярное произведение равно нулю. Запишем скалярное произведение : — 2x + 12 = 0, отсюда x = 6.
1)углы при основании равны т. К. треугольник р / б. (равнобедренный) 2)вершина = 180 — внешний угол = 180 — 130 = 50т. К. они смежные 3)любой угол при основании = (180 — 50) : 2 = 65т. К углы при основании равны и сумма углов треугольника = 180 О..
Вот весь ответ. Надеюсь, помогла.
Ответ 2) в ромб1 из углов равен 90 то квадр.
Сначала проводим касательную к окружности, затем хорду и радиус ОС. Схема и расчет — в приложении.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Правильный многоугольник
Видео:Задание 1. Часть 3. Окружность.Скачать

Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a 1 = a 2 = a 3 = … = a n-1 = a n ,
α 1 = α 2 = α 3 = … = α n-1 = α n
где a1 … an — длины сторон правильного многоугольника,
α 1 … α n — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
- Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольникаO.
- Сумма всех углов n-угольника равна: 180° · n — 2
- Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .
Видео:Периметр правильного шестиугольника равен 150. Найдите диаметр описанной около него окружности (ЕГЭ)Скачать

Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a = 2 · r · tg 180° n (через градусы),
a = 2 · r · tg π n (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a = 2 · R · sin 180° n (через градусы),
a = 2 · R · sin π n (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r = a : 2 · tg 180° n (через градусы),
r = a : 2 · tg π n (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R = a : 2 · sin 180° n (через градусы),
R = a : 2 · sin π n (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
Формула площади n-угольника через радиус вписанной окружности
Формула площади n-угольника через радиус описанной окружности
Формула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
Формула площади правильного треугольника через длину стороны
Формула площади правильного треугольника через радиус вписанной окружности
Формула площади правильного треугольника через радиус описанной окружности
Углы между сторонами правильного треугольника
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
Углы между сторонами правильного четырехугольника
Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности
Углы между сторонами правильного шестиугольника
Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
Четырехугольник, вписанный в окружность — основные свойства, признаки и формулы
Общие сведения
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр
Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2 .
Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2 .
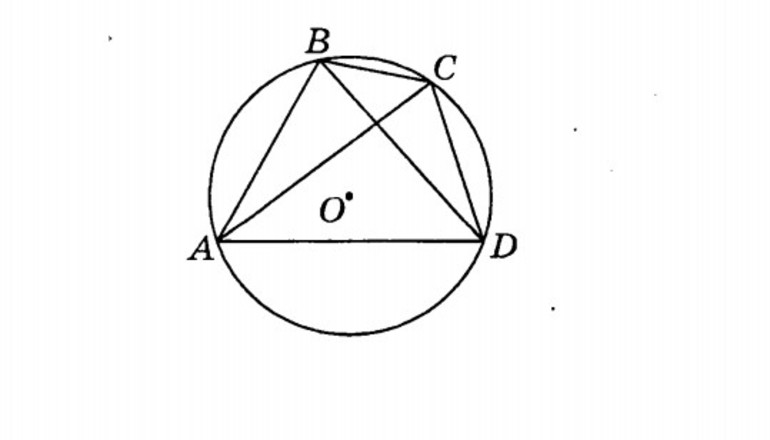
Диагонали и углы
Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2 .
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
В круг радиуса R вписан правильный треугольник. В круг наудачу брошена точка. Найти вероятность того, что эта точка окажется внутри треугольника
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,909
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
В окружность радиуса r вписан правильный
Вопрос по геометрии:
В окружность радиуса R вписан правильный четырехугольник. Найдите его площадь.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Правильный четырехугольник — это квадрат, значит в окружность вписан квадрат. Диагональ квадрата является диаметром окружности. Диагонали квадрата пересекаются пол прямым углом и делят квадрат на 4 равных прямоугольных треугольника, катеты которых раны радиусу описанной около квадрата окружности, т.е.R. Тогда площадь квадрата равна площади 4 треугольников.
S=4*1/2*R*R=2
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Контрольная работа по геометрии 9 класс, по теме «Правильные многоугольники».
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
1.а) Найдите длину окружности, радиус которой равен 7см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 12см.
в) Длина дуги окружности равна 3 π , а ее радиус равен 8. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 10см и 24см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5 см.
4. Около правильного четырехугольника описана окружность радиуса 12см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 9см.
б)Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 54π, а градусная мера дуги равна 60º.
2. Прямоугольный треугольник с катетами 9см и 12см вписан в окружность. Найдите длину окружности и площадь круга.
3 Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 6 см.
4. Дан правильный треугольник со стороной 18см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 5см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 14см.
в) Длина дуги окружности равна 6 π , а ее радиус равен 12. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 6см и 8см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 16 см.
4. Около правильного четырехугольника описана окружность радиуса 8см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 11см.
б)Найдите длину дуги окружности радиуса 5см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 100π, а градусная мера дуги равна 40º.
2. Прямоугольный треугольник с катетами 16см и 30см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 14 см.
4. Дан правильный треугольник со стороной 15см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 24 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 7см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 12см.
в) Длина дуги окружности равна 3 π , а ее радиус равен 8. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 10см и 24см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5 см.
4. Около правильного четырехугольника описана окружность радиуса 12см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 9см.
б)Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 54π, а градусная мера дуги равна 60º.2. Прямоугольный треугольник с катетами 9см и 12см вписан в окружность. Найдите длину окружности и площадь круга.
3 Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 6 см.
4. Дан правильный треугольник со стороной 18см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 7см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 12см.
в) Длина дуги окружности равна 3 π , а ее радиус равен 8. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 10см и 24см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5 см.
4. Около правильного четырехугольника описана окружность радиуса 12см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 9см.
б)Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 54π, а градусная мера дуги равна 60º.
2. Прямоугольный треугольник с катетами 9см и 12см вписан в окружность. Найдите длину окружности и площадь круга.
3 Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 6 см.
4. Дан правильный треугольник со стороной 18см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 5см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 14см.
в) Длина дуги окружности равна 6 π , а ее радиус равен 12. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 6см и 8см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 16 см.
4. Около правильного четырехугольника описана окружность радиуса 8см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 11см.
б)Найдите длину дуги окружности радиуса 5см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 100π, а градусная мера дуги равна 40º.
2. Прямоугольный треугольник с катетами 16см и 30см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 14 см.
4. Дан правильный треугольник со стороной 15см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 24 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 7см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 12см.
в) Длина дуги окружности равна 3 π , а ее радиус равен 8. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 10см и 24см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5 см.
4. Около правильного четырехугольника описана окружность радиуса 12см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 9см.
б)Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 54π, а градусная мера дуги равна 60º.2. Прямоугольный треугольник с катетами 9см и 12см вписан в окружность. Найдите длину окружности и площадь круга.
3 Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 6 см.
4. Дан правильный треугольник со стороной 18см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 5см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 14см.
в) Длина дуги окружности равна 6 π , а ее радиус равен 12. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 6см и 8см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 16 см.
4. Около правильного четырехугольника описана окружность радиуса 8см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 11см.
б)Найдите длину дуги окружности радиуса 5см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 100π, а градусная мера дуги равна 40º.
2. Прямоугольный треугольник с катетами 16см и 30см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 14 см.
4. Дан правильный треугольник со стороной 15см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 24 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 5см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 14см.
в) Длина дуги окружности равна 6 π , а ее радиус равен 12. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 6см и 8см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 16 см.
4. Около правильного четырехугольника описана окружность радиуса 8см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 11см.
б)Найдите длину дуги окружности радиуса 5см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 100π, а градусная мера дуги равна 40º.
2. Прямоугольный треугольник с катетами 16см и 30см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 14 см.
4. Дан правильный треугольник со стороной 15см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 24 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
1.а) Найдите длину окружности, радиус которой равен 5см.
б)Найдите площадь кругового сектора, если градусная мера дуги равна 120 градусам, а радиус круга равен 14см.
в) Длина дуги окружности равна 6 π , а ее радиус равен 12. Найдите градусную меру этой дуги.
2. Прямоугольник со сторонами 6см и 8см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 16 см.
4. Около правильного четырехугольника описана окружность радиуса 8см.Найдите радиус вписанной окружности, площадь, периметр этого четырехугольника.
5. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.
1. а)Найдите площадь круга, радиус которого равен 11см.
б)Найдите длину дуги окружности радиуса 5см, если ее градусная мера равна 150º.
в) Найдите радиус окружности, если площадь кругового сектора равна 100π, а градусная мера дуги равна 40º.
2. Прямоугольный треугольник с катетами 16см и 30см вписан в окружность. Найдите длину окружности и площадь круга.
3. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, вписанного в окружность равна 14 см.
4. Дан правильный треугольник со стороной 15см. Найдите радиус вписанной в него окружности и описанной около него, площадь и периметр этого треугольника.
5 Периметр квадрата, описанного около окружности, равен 24 дм. Найдите периметр правильного треугольника, вписанного в эту же окружность.
В окружность радиуса 12 см вписан правильный треугольник. Вычислите: а) высоту треугольника; б) расстояние от центра окружности цо прямой, содержащей
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.