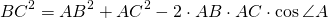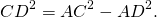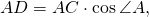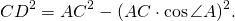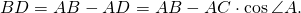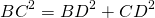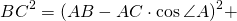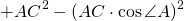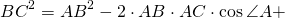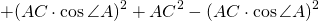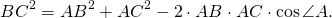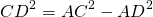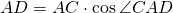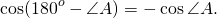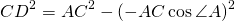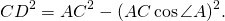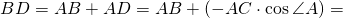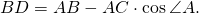Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.» — неверно, квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2) «Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.» — верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
3) «Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.» — верно, остроугольным называется треугольник у которого все углы меньше 90°.
4) «В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.» — верно, по теореме Пифагора.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Теорема косинусов
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
- a² = b² + c² – 2b.c.cosα
- b² = a² + c² – 2a.c.cosβ
- c² = a² + b² – 2a.b.cosγ
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)
a² = 12² + 8² – 2×12×8×(- 1/2)
Длина третьей стороны — примерно 17,436 см.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
- b²+c²−a² 0, значит угол α — острый.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.
2. Вычитаем это из стороны b, так мы получим DA:
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
- две его стороны равны;
- углы при основании равны.
Используем формулу теоремы косинусов
a² = b² + c² – 2b.c.cosα
Подставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
Видео:КЛАССИКА ЖАНРА! Гениальный способ.Скачать

Теорема синусов
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:
Видео:Как найти площадь треугольника без формулы?Скачать

Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
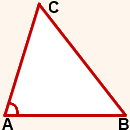
1) Опустим перпендикуляр CD на сторону AB.
2) Рассмотрим прямоугольный треугольник ADC.
По теореме Пифагора,
По определению косинуса острого угла в прямоугольном треугольнике,
3) Рассмотрим прямоугольный треугольник BDC.
По теореме Пифагора
II. Если треугольник ABC — тупоугольный.
1) Опускаем перпендикуляр CD на прямую, содержащую сторону AB.
2) Рассмотрим прямоугольный треугольник ADC.
По теореме Пифагора,
По определению косинуса,
Так как углы A и CAD — смежные, то ∠CAD=180º-∠A. По формуле приведения
3) Рассмотрим прямоугольный треугольник BDC.
Дальнейшая часть доказательства полностью повторяет рассуждения пункта I.
III. Если треугольник ABC — прямоугольный, где ∠A=90º, получаем теорему Пифагора (cos90º=0).
🎦 Видео
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Формулы равностороннего треугольника #shortsСкачать

Теорема Пифагора для чайников)))Скачать

Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Задание 9 ОГЭ от ФИПИСкачать

Задача мозгового штурмаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Хитрый периметрСкачать

Простая геометрияСкачать

Площади треугольников с равным углом.Скачать