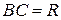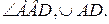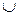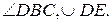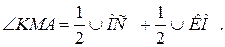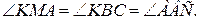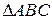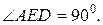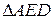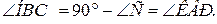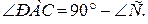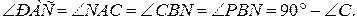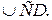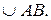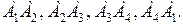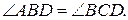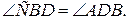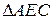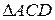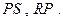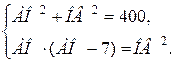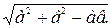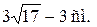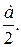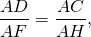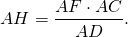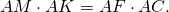Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.
$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Докажем, например, утверждение $$ 4.^$$ .
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
| `d^2=c^2+ab`. |
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).
По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`
(т. к. угол `BDK` — это угол между диагоналями трапеции).
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.
$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.
Видео:ВСЕ правила и формулы ПЛАНИМЕТРИИСкачать

III.3. Задачи к теоретической карте № 3
№ 1.
 1. 1. | 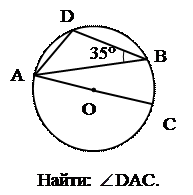 2. 2. | 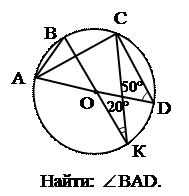 3. 3. | ||
 4. 4.
| 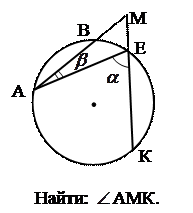 5. 5. | 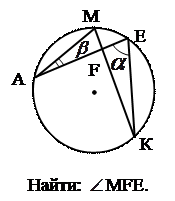 6. 6. |
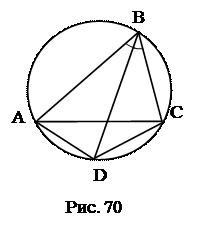
№2.Биссектриса угла В треугольника АВС пресекает описанную окружность в точке D. Доказать, что треугольник АDC равнобедренный.
1. 
2. 
Используемые факты из теоретической карты: 1.2.
№3.Доказать, что сторона треугольника, лежащая против угла в 30 0 , равна радиусу окружности, описанной около треугольника.
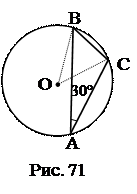
1. 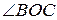
2. Вид 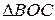
3.
Используемые факты из теоретической карты:
№4. Угол при вершине равнобедренного треугольника равен 40°. Одна из
боковых сторон служит диаметром полуокружности, которая делится другими сторонами на три дуги. Найти градусные меры этих дуг.
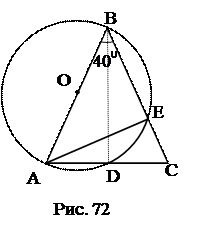
1. BD 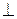
2.
3.
4.
Ответ: 40 0 , 40 0 , 100 0
Используемые факты из теоретической карты: 1.2.
№5. Через вершины Ви С треугольника АВС проходит окружность, пересекающая стороны АВ и АС в точках К и М соответственно. Доказать, что ∆АВС
∆АМК. Найти МК и АМ, если АВ=2, ВС=4, АС=5, АК=1.
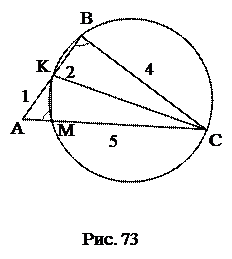
1. Проведем 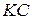
2. 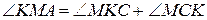
3.
4.
5.
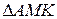
6. МК. 7. АМ. Ответ: 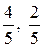
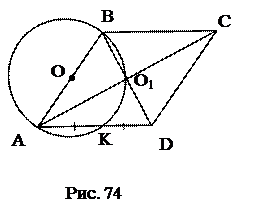
Используемые факты из теоретической карты: 1.2.№6. Окружность, построенная на стороне параллелограмма как на диаметре, проходит через середину соседней стороны и точку пересечения диагоналей. Найти углы параллелограмма.
1. 
2. 
3. 
4. 
Ответ: 60 0 , 120 0 .
Используемые факты из теоретической карты: 1.2.
№7. Окружность, построенная на большем основании трапеции как на диаметре, касается меньшего основания и пересекает боковые стороны, деля их пополам. Найти меньшее основание трапеции, если радиус окружности равен R.
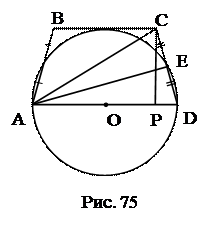
проведем АЕ, 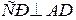
1.
2.
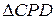
3. CP = R, PD = R – OP.
4. ∆CPD: OP 2 + 2R∙OP – 2R 2 =0, 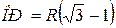
5. Трапеция ABCD – равнобедренная. ВС = 2ОР.
Ответ: 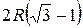
Используемые факты из теоретической карты: 1.2.
№8. Высоты остроугольного треугольника продлены до пересечения с описанной окружностью. Доказать, что отрезки этих линий от ортоцентра до окружности делятся соответственными сторонами пополам.
Точка К – ортоцентр треугольника АВС.
1. ∆ВНС:
2. ∆АРС:
3.
4. 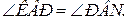
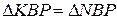
Аналогично доказывается, что 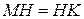
Используемые факты из теоретической карты: 1.2.
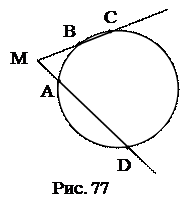
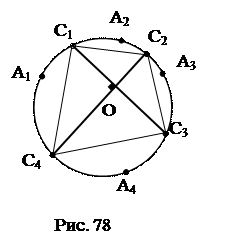
№9.Окружность разделена точками A, B, C и D так, что 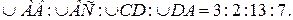
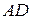
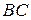
1.
2.
3. 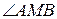
Используемые факты из теоретической карты: 1.3.
№10. На окружности взяты четыре точки. Середины образованных дуг попарно соединены отрезками. Доказать, что среди этих отрезков есть, по крайней мере, два перпендикулярных.
1. Выразить 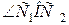

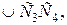
2.
Используемые факты из теоретической карты: 1.4.
№11. В окружность вписан четырехугольник. Его противоположные стороны CD и АВ, ВС и AD продолжены до взаимного пересечения в точках N и F. Доказать, что биссектрисы углов BFA и AND перпендикулярны.
1. 
2. 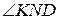
3.
4. 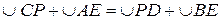
5. 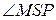
6. 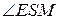
7. 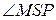
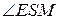
Используемые факты из теоретической карты:
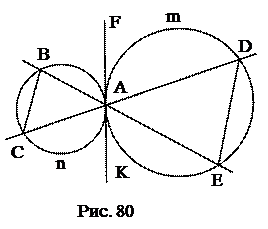
№12. Через точку касания двух окружностей проведены две секущие, концы которых соединены хордами. Доказать, что эти хорды параллельны.

2. 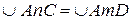
3. 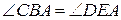
Используемые факты из теоретической карты: 1.2; 1.5.
№13.В треугольнике АВС проведены высоты ВВ1 и СС1. Доказать, что
касательная в точке А к описанной окружности параллельна прямой В1С1.

Используемые факты из теоретической карты: 1.5.
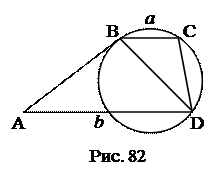
№14. Окружность проходит через вершины В, С, D трапеции ABCD и касается боковой стороны АВ в точке В. Основания трапеции а и b. Найти диагональ BD.
2.
3.
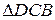
4. 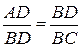
5. 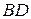
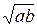
Используемые факты из теоретической карты: 1.2; 1.5.
№15. Из точки С окружности на хорду АВ опущен перпендикуляр CD. Из концов хорды опущены перпендикуляры АЕ и BF на касательную к окружности в точке С. Доказать, что 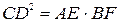
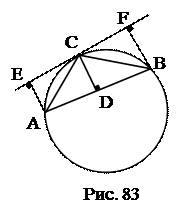
1.
2. 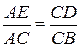
4.
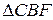
5. 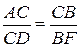
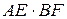
Используемые факты из теоретической карты: 1.2; 1.5.
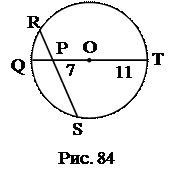
№16. Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см.
Через эту точку проведена хорда длиной 18 см. Каковы длины отрезков, на
которые делится хорда точкой Р?

2. 
3. 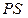
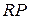
4. 
5.
Ответ: 6 и 12. Используемые факты из теоретической карты: 2.1.
№17. АС и ВD – диагонали ромба АВCD. Окружность описанная около
треугольника ABD, пересекает большую диагональ АС в точке Е. Определить диагонали ромба, если АВ = 20 см, СЕ = 7 см.
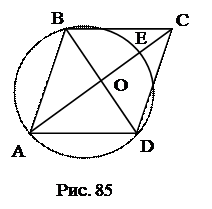
1. АО 2 +ОВ 2 =АВ 2 .
2. АО∙ОЕ=ОВ 2 , АО∙(АО – ЕС) = ОВ 2 .
3. Решить систему уравнений
Ответ: 32 см, 24 см.
Используемые факты из теоретической карты: 2.1.
№ 18.Через точку Р диаметра АВ данной окружности проведена хорда CD, образующая с диаметром АВ угол 60°. Вычислить радиус окружности R, если
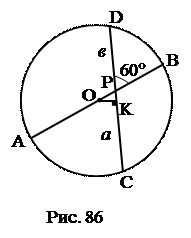
1.СК. 2. КР. 3. ОР ( 
4. Выразить АР через ОР и R.
5. Выразить РВ через ОР и R.
6.Составить равенство АР·РВ = СР·РD.
7.Выразить R из составленного равенства.
Ответ:
Используемые факты из теоретической карты: 2.1;
№19. Из внешней точки проведена к окружности секущая длиной 12 см и
касательная, длина которой составляет два внутренних отрезка секущей.
Определить длину касательной.
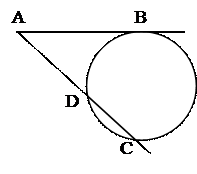
1. Выразить AD через АС и DС.
2. Выразить АВ через DС.
3. Составить уравнение.
|
4. DС. 5. АВ.
Ответ:
Используемые факты из теоретической карты: 2.2.
№20. Полуокружность, построенная на меньшем катете, как на диаметре, делит биссектрису острого угла, прилежащего к этому катету, в отношении 1:3. Найти углы треугольника.
1. КС – касательная, КВ – секущая,
выразить КС (в частях).
2. sin
3. 
Используемые факты из теоретической карты: 2.2.
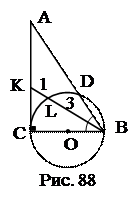
№21. Катеты прямоугольного треугольника равны а и b. На отрезках гипотенузы, определенных основанием перпендикуляра, опущенного на гипотенузу из
вершины прямого угла, описаны как на диаметрах окружности. Найти длины отрезков катетов, находящихся внутри этих окружностей.
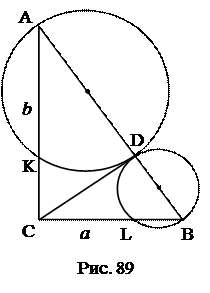
1. 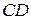
2. КС (СD – касательная, СА – секущая).
4. Аналогично LB.
Ответ: 
№22. На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М, а
боковую сторону ВС в точке N. Найти длины отрезков СN и NM, если
АС=а, АВ=b.
План решения.
1. 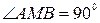
2. 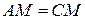
3. 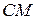
Ответ: 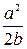
Используемые факты из теоретической карты: 1.2; 2.3.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

На стороне треугольника как на диаметре построена окружность
На стороне BC остроугольного треугольника ABC (AB≠BC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC.
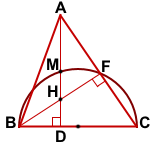
AD=49, AD и BF — высоты, AD ∩ BF=H,
полуокружность с диаметром BC пересекает AD в точке M, MD=42
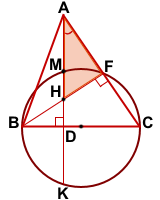
Точка F лежит на окружности ( если вписанный угол — прямой, то он опирается на диаметр).
Прямоугольные треугольники ADC и AFH подобны по общему острому углу A.
Из подобия треугольников следует пропорциональность соответствующих сторон:
По свойству секущих, проведённых из одной точки,
DK=MD=42 (так как диаметр BC перпендикулярен хорде MK, то он проходит через её середину).
💡 Видео
На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задание второй части реального варианта ЕГЭ 2015 Планиметрия #3Скачать

На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

№1,16 Планиметрия из ЕГЭ по профильной математике. Теория и важные конструкции | "Щелчок"Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Трапеция и вписанная окружностьСкачать

Вариант ФИПИ на 100 баллов #4 (математика ЕГЭ профиль)Скачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

ЕГЭ Математика Задание 6#27935Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Подготовка к ЕГЭ по математике. Задача №16 - Планиметрия. Занятие №2Скачать

БОМБИЧЕСКАЯ ЗАДАЧА!Скачать

окружности огэ по математике 2023 / маттаймСкачать

Профильный ЕГЭ 2022 математика - задача 16 планиметрия. Летняя школа #5Скачать

 АDВ .
АDВ .