Пример:
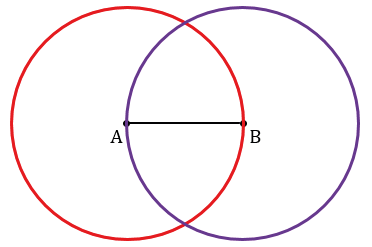
Дано: отрезок АВ.
Построить: середину АВ.
Решение:
Строим с помощью линейки произвольный отрезок АВ.
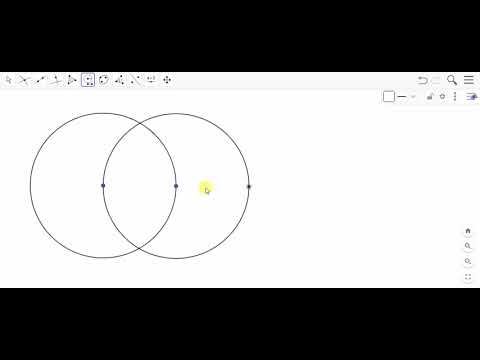
Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.
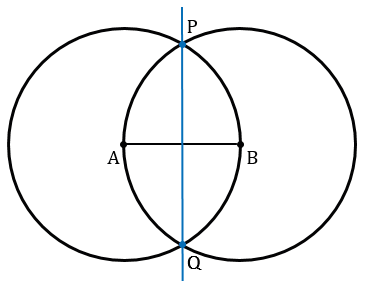
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.
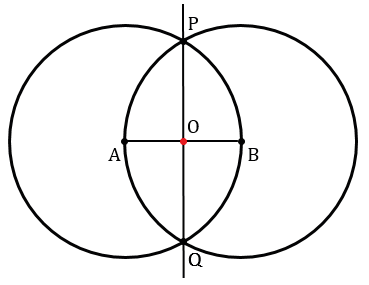
Точку пересечения прямой РQ и отрезка АВ обозначим О.
Докажем, что точка О — искомая точка, т.е. точка О — середина отрезка АВ.
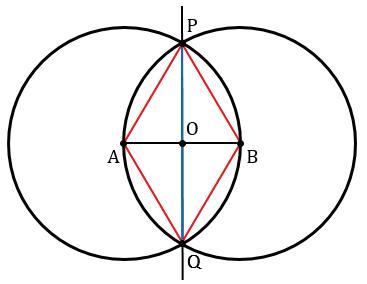
Рассмотрим треугольники РАQ и РВQ.
По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ — общая, следовательно, 


В 


Поделись с друзьями в социальных сетях:
- Урок№2 Тема: Построение середины отрезка. Построение перпендикулярных прямых
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Планиметрия (прямая и окружность)
- 1.1 Построить угол 60° с заданой стороной
- 1.2 Построить серединный перпендикуляр к отрезку
- 1.3 Середина отрезка
- 1.4 Окружность, вписанная в квадрат
- 1.6 Найти центр окружности
- 1.7 Квадрат, вписанный в окружность
- Задача Наполеона
- 🎥 Видео
Видео:Построение перпендикулярных прямых.7 классСкачать

Урок№2 Тема: Построение середины отрезка. Построение перпендикулярных прямых
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Построение середины отрезкаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Тема : Построение середины отрезка. Построение перпендикулярных прямых
обучающая: научить учащихся с помощью циркуля и линейки выполнять деление отрезка пополам; сформировать умения и навыки построения перпендикулярных прямых;
развивающая: развитие пространственного мышления, внимания;
воспитательная: воспитание трудолюбия и аккуратности.
1. Актуализация основных теоретических понятий (5мин).
Сначала можно провести фронтальный опрос по следующим вопросам:
1. Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?
2. Какой треугольник называется равнобедренным? Как называются его стороны?
3. Какой треугольник называется равносторонним?
4. Что называют серединой отрезка?
Далее предложить задание: с помощью циркуля и линейки построить биссектрису, выходящую из вершины равнобедренного треугольника. Перечислить ее свойства.
2. Изучение нового материала (практическая работа) (20мин)
Построение середины отрезка
При изучении нового материала используется таблица№4 приложения 4, по которой учащиеся составляют рассказ, как разделить данный отрезок пополам. После этого в тетрадях выполняются соответствующие построения.
Задача . Построить середину данного отрезка (объясняет учитель с помощью учащихся).
Решение . Пусть АВ — данный отрезок. Построим две окружности с центрами А и В радиуса АВ (рис.5).
Они пересекаются в точках Р и Q. Проведем прямую РQ. Точка О пересечения этой прямой с отрезком АВ и искомая середина отрезка АВ.
В самом деле, треугольники АРQ и ВРQ равны по трем сторонам, поэтому 1=2.
Следовательно, отрезок РО — биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т.е. точка О — середина отрезка АВ.
Построение перпендикулярных прямых
Здесь необходимо обратить внимание, что возможны два случая:
1. Точка принадлежит прямой;
2. Точка не принадлежит прямой.
После повторения учитель формулирует задачу и объясняет построение для первого случая, при этом может быть использована таблица№3 приложения 4.
При рассмотрении второго случая учащиеся при помощи таблицы 4 проводят построение и доказательство самостоятельно.
Задача . Через данную точку О провести прямую, перпендикулярную данной прямой а (объясняет учитель, после обсуждения с учениками).
Решение . Возможны два случая:
1) точка О лежит на прямой а;
2) точка О не лежит на прямой а.
Рассмотрим первый случай (рис.6). Из точки О проводим произвольным радиусом окружность. Она пересекает прямую а в двух точках: А и В. из точек А и В проводим окружности радиусом АВ. Пусть С — точка их пересечения. Искомая прямая проходит через точки О и С.
Перпендикулярность прямых ОС и АВ следует из равенства углов при вершине О треугольников АСО и ВСО.
Эти треугольники равны по третьему признаку равенства треугольников.
Рассмотрим построение и доказательство для второго случая (рис.7).
Из точки О проводим окружность, пересекающую прямую а. Пусть А и В — точки ее пересечения с прямой а. Из точек А и В тем же радиусом проводим окружности. Пусть О — точка их пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка О. Искомая прямая проходит через точки О и О. Докажем это. Обозначим через С точку пересечения прямых АВ и ОО. Треугольники АОВ и АОВ равны по третьему признаку. Поэтому угол ОАС равен углу ОАС. А тогда треугольники ОАС и ОАС равны по первому признаку. Значит, их углы АСО и АСО равны. А так как они смежные, то они прямые. Таким образом, ОС — перпендикуляр, опущенный из точки О на прямую а.
3. Закрепление (10 мин)
Задача. Постройте прямоугольный треугольник по его катетам.
Данную задачу ученик решает у доски, предварительно проведя ее анализ.
Выполним чертёж — набросок (рис.8).
2. Построение (рис.9).
1. На прямой отметим точку С и отложим отрезок СВ=а.
2. Построим прямую, проходящую через точку С перпендикулярную СВ.
3. Отложим отрезок СА=b
В АВС ВС=а, СА= b, ВDАС, следовательно, угол ВСА равен 90є. Значит треугольник АВС — искомый.
Также для отработки умений и навыков, можно использовать задачи №154 (а, б) (см. приложение 1).
4. Подведение итога (3мин)
1. В ходе урока мы решили две задачи на построение. Учились:
а) строить середину отрезка;
б) строить перпендикулярные прямые.
2. В ходе решения этих задач:
а) вспомнили признаки равенства треугольников;
б) использовали построения окружностей, отрезков, лучей.
5. На дом (2мин): №153 (см. приложение 1).
Тема: Решение задач на построение
обучающая: отработка умений и навыков выполнения элементарных построений с помощью циркуля и линейки;
развивающая: развитие пространственного мышления, внимания;
воспитательная: воспитание трудолюбия и аккуратности.
1. Проверка домашнего задания (10мин)
Проверить выполнение задачи №153.
Проверку можно организовать так: у доски три ученика, они должны построить прямую, проходящую через точку А перпендикулярно прямой а (рис.10).
Класс в это время может выполнить задание: дан треугольник АВС. построить высоту АD. После выполнения задания каждый шаг построения должен быть прокомментирован и обоснован.
2. Самостоятельная работа
Самостоятельная работа проводится по трём вариантам и имеет контролирующий характер
1. Разделить отрезок на 4 равные части.
2. Дан АВС. Построить биссектрису ВК.
3. Дан угол АОВ. Построить угол, для которого луч ОВ является биссектрисой.
Видео:Построение середины отрезкаСкачать

Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
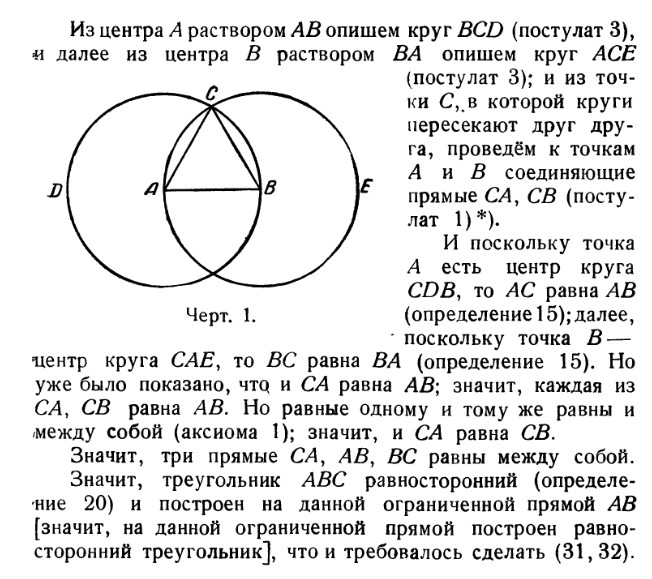
На данной ограниченной прямой построить равносторонний треугольник
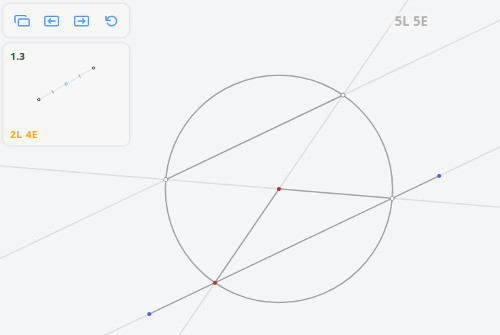
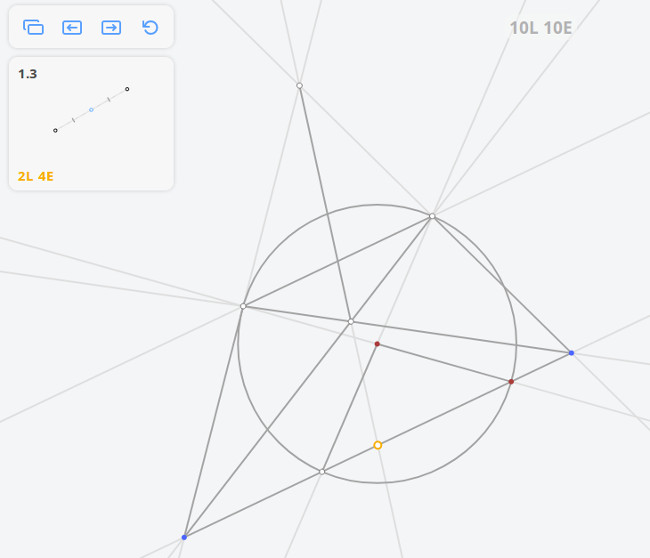
1.3 Середина отрезка
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
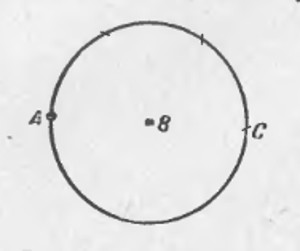
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
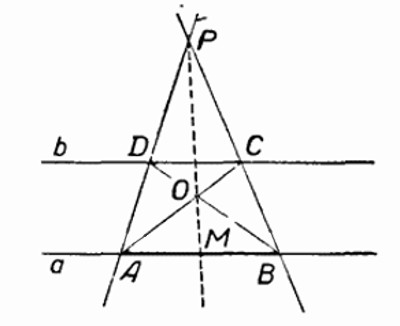
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
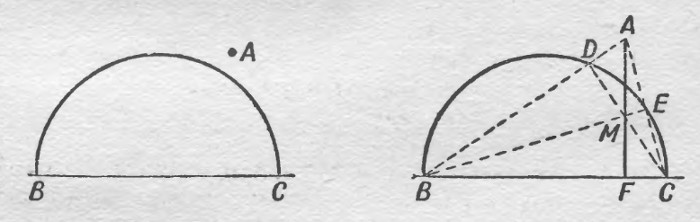
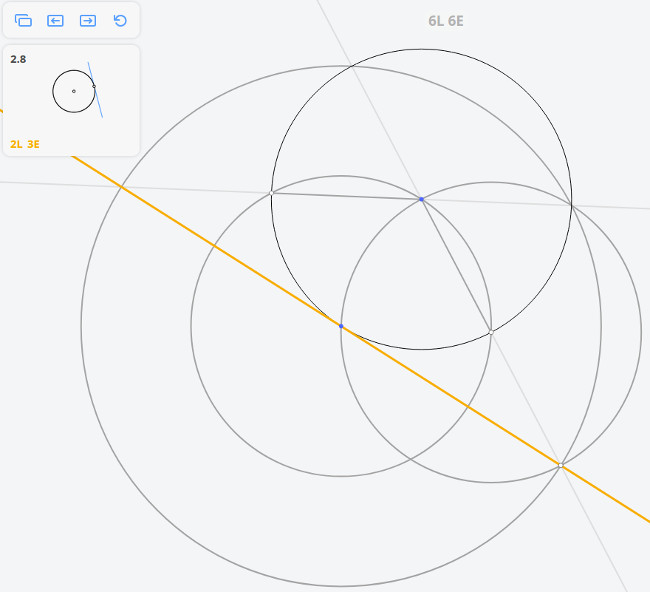
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
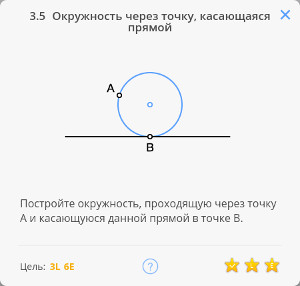
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
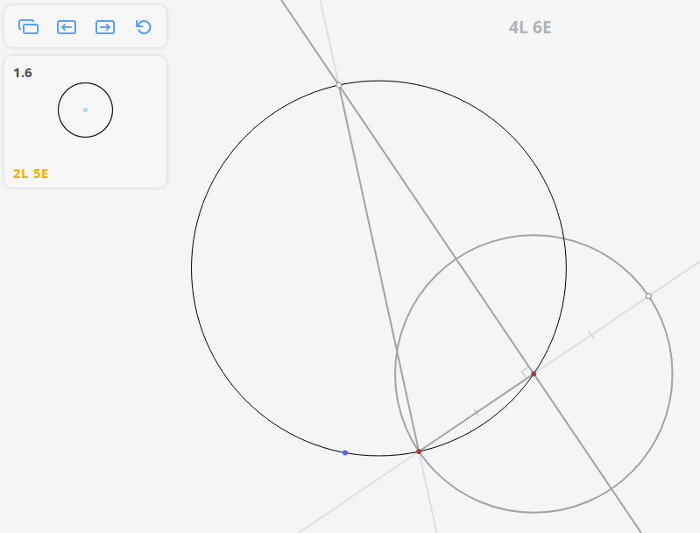
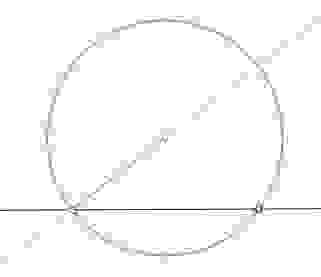
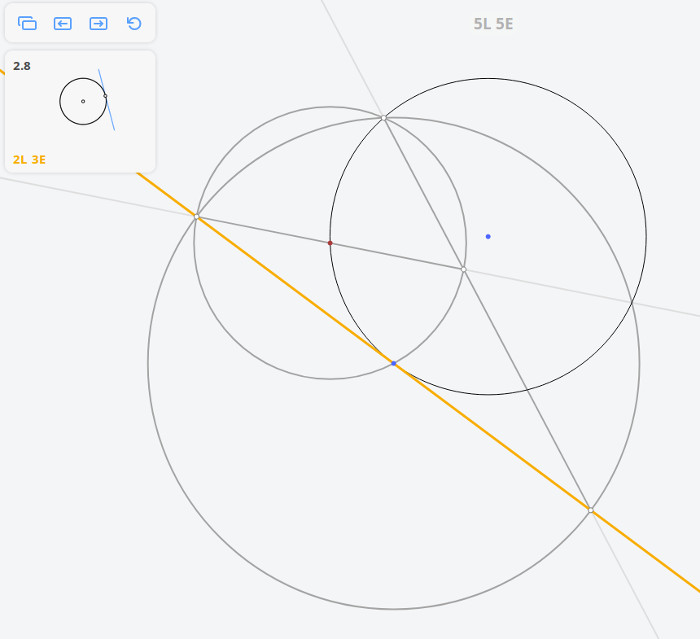
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
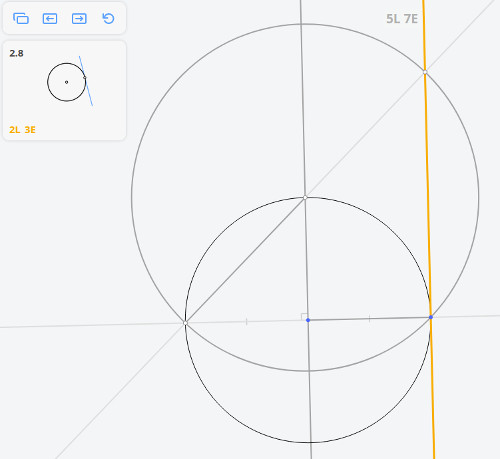
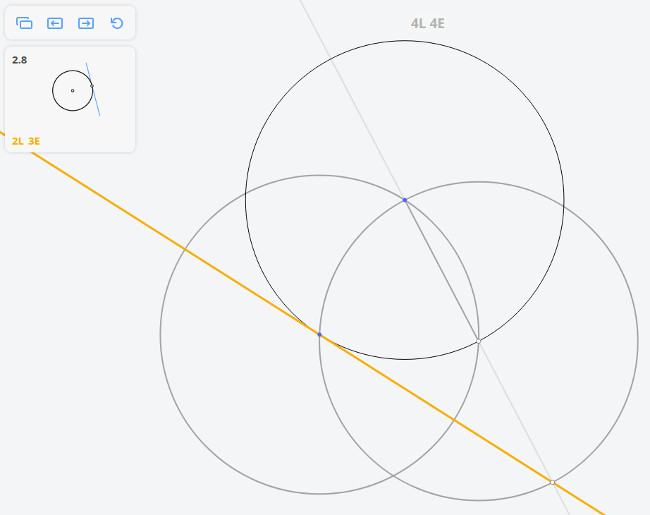
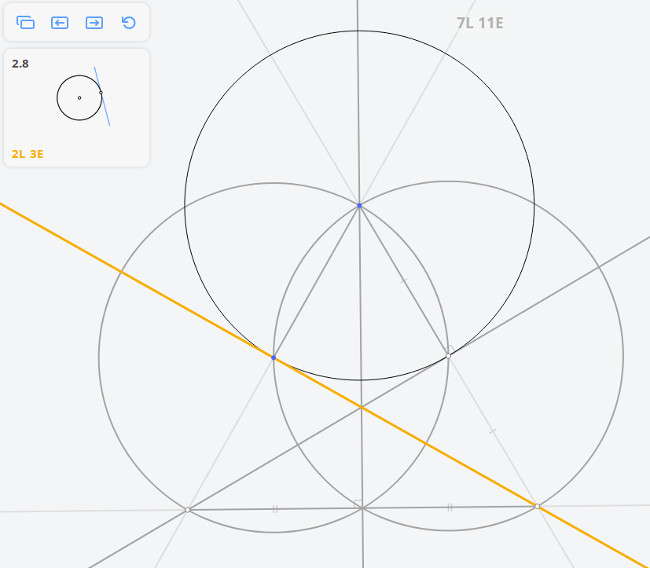
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
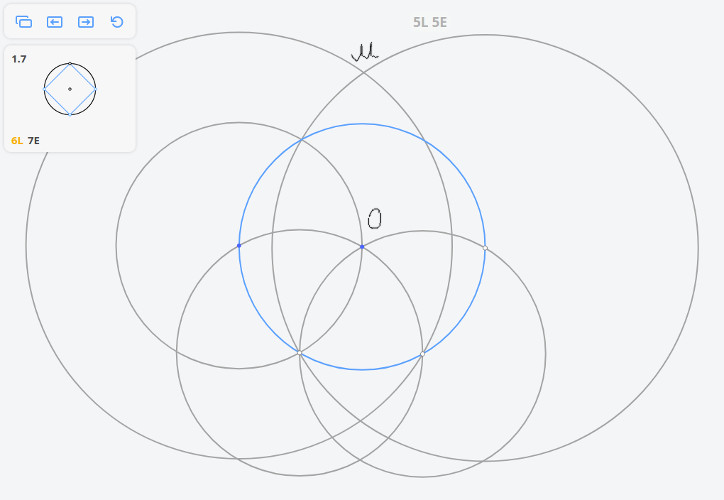
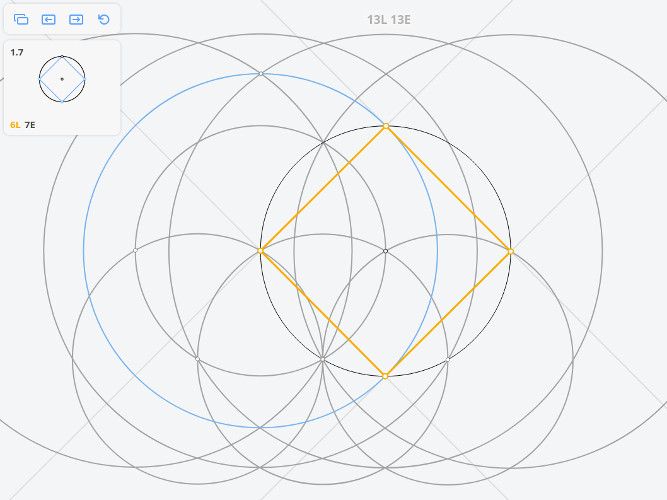
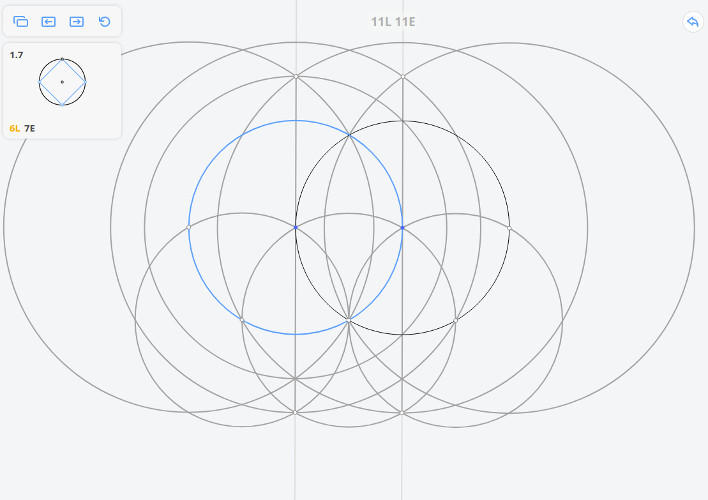
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО
🎥 Видео
Построение середины отрезкаСкачать

7 класс, 23 урок, Примеры задач на построениеСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Построение середины отрезка. Геометрия 7 класс.Скачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Построение угла, равного данному. 7 класс.Скачать

Построение середины отрезка, окончательный вариантСкачать

Построение середины отрезкаСкачать
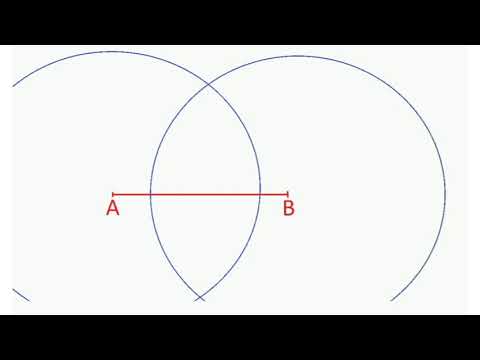
Построение перпендикулярных прямыхСкачать

Построение биссектрисы углаСкачать

Построение серединного перпендикуляра. Деление отрезка пополамСкачать

Построение угла равного данномуСкачать

Построение середины отрезкаСкачать

Построение биссектрисы угла. 7 класс.Скачать

Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

Построение середины отрезка только циркулемСкачать
7 класс. Геометрия. Урок 9. Задачи на построение: теорияСкачать