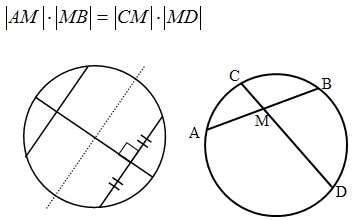
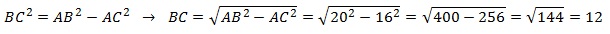Прототипы заданий 16 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 16 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (окружность, круг и их элементы )
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 16 с ответами → скачать |
| Прототипы задания 16 ОГЭ по математике (окружности) Опубликовано: Гармс Людмила Павловна → скачать |
| Материалы для отработки задания 16 Автор: Е. А. Ширяева → задания |
| Задания 16 — практика Решение типовых задач № 16 на ОГЭ по математике Содержание
Видео:Задание 16 (часть 1) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать  Окружность круг их элементы часть 1 фипи ответыВ окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны. На эти хорды опущены перпендикуляры ОК и OL. Докажите, что ОК и OL равны. Треугольники АОВ и СОD равны по двум сторонам и углу между ними (AO = BO = CO = DO как радиусы окружности, ∠AOB = ∠COD по условию). Следовательно, высоты OK и OL равны как соответственные элементы равных треугольников. Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны. Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J . Значит, IJ — серединный перпендикуляр к AB. Задание 25 № 341422 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны. Решение: IA и IB — радиусы окружности с центром в точке I => IA = IB => треугольник IAB — равнобедренный. Проведем медиану IJ к стороне AB. Т.к. треугольник IAB — равнобедренный, то IJ также является высотой, проведённой AB => AB и IJ перпендикулярны, что и требовалось доказать. В окружности с центром O проведены две равные хорды Проведем ОK, ON, OL, OM — радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать. В окружности через середину O хорды AC проведена хорда BD так, что дуги AB и CD равны. Докажите, что O — середина хорды BD. Вписанные углы ADB, CBD , ACB и DAC опираются на равные дуги, значит, они равны. Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен AO:OC. Поскольку AO = OC , эти треугольники равны, следовательно, BO = OD. Окружности с центрами в точках O1 и O2 не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n. Проведём построения и введём обозначения, как показано на рисунке. Пусть Видео:Задание 16 ОГЭ 2023 математика | Окружность, круг и их элементыСкачать  Задание №17 ОГЭ по математикеВидео:Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать  Окружность, круг и их элементыВ 17 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей. Ответом в задании 17 является целое число или конечная десятичная дробь. Теория к заданию №17Несмотря на то, что в задании №17 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность». Начнем рассмотрение с понятия вписанная окружность:
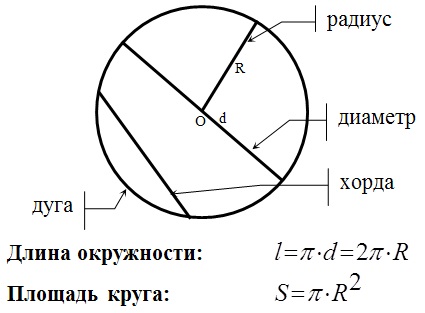
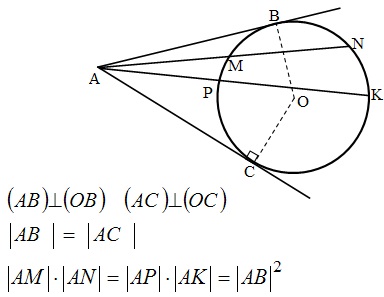
Длинна окружности и площадь: Касательная и секущая:
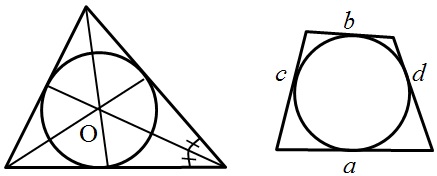
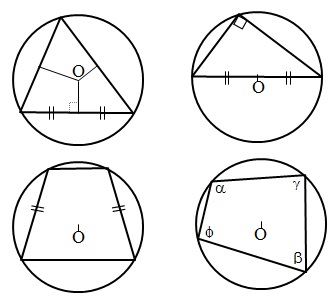
Описанная окружность и её свойства:
Хорда – отрезок, соединяющий две точки окружности.
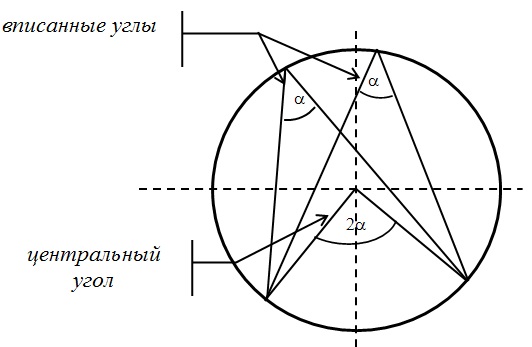
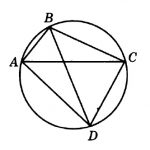
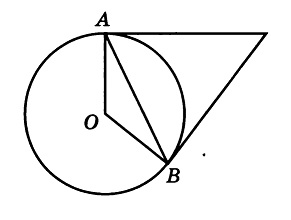
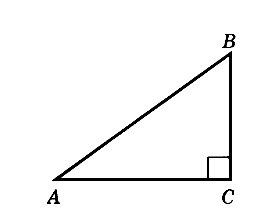
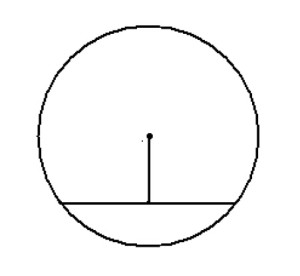
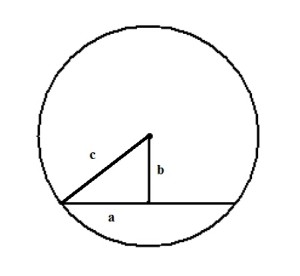
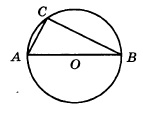
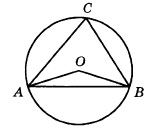
Центральный и вписанный углы: Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии. Разбор типовых вариантов заданий №17 ОГЭ по математикеПервый вариант заданияЧетырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах. Решение:Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD: ∠ABD = 92 — 60 = 32 Второй вариант заданияКасательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах. Решение:Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны: Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов. Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен: Третий вариант заданияВ треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности. Решение:Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом. По теореме Пифагора найдем гипотенузу AB: AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400 Гипотенуза равна 20, значит радиус — 10. Демонстрационный вариант ОГЭ 2019Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см. Решение:Для решения данной задачи необходимо провести радиус окружности к точке начала хорды: Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a: a² = c² — b² = 13² — 5² = 169 — 25 = 144 Но а — лишь половина хорды, поэтому вся хорда равна 2 • а = 24 Четвертый вариант заданияЦентр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 10. Найдите ВС, если АС=16. Решение:Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90 0 , и, следовательно, ∆АСВ прямоугольный. Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора АС 2 +ВС 2 =АВ 2 (1) По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20. Тогда из (1) получим: Пятый вариант заданияТреугольник АВС вписан в окружность с центром в точке О. Найдите угол АСВ, если угол АОВ равен 113 0 . Ответ дайте в градусах. Решение:Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113 0 . Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=113 0 , то угол АСВ равен 🌟 ВидеоОкружность. Круг. 5 класс.Скачать  Задание 16 (часть 2) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать  ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать  Задание 16.Окружность, круг и их элементы. Часть 1Скачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  ОГЭ по математике 2019. Задание 17. Окружность, круг и их элементы. Теория+задачи (часть 1)Скачать  Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать  Задание №17 ОГЭ. Окружность, круг и их элементы.Скачать  ЕГЭ. Математика. Окружность, круг и их элементы. ПрактикаСкачать  Задание 16 (часть 3) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать  Задание 6. Часть 3. Окружность, круг и их элементыСкачать  ОГЭ Задание 16 Окружность, круг и их элементы (Часть 3)Скачать  ОГЭ Задание 16 Окружность, круг и их элементы (Часть 4)Скачать  Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать  Окружность и круг, 6 классСкачать  Математика. 3 класс. Окружность, круг и их элементы /24.11.2020/Скачать  Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать  |